Криптографические методы защиты информации - ответы
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ВЕЧЕРОК
или ШАШЛЫКИ
- устойчивее к действию этой программы?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101000001101110011110000.
, построить контрольную сумму для сообщения 1101000001101110011110000.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=29, x=10.
Чей компьютер он взломает быстрее?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1011110001000101010010111.
, построить контрольную сумму для сообщения 1011110001000101010010111.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=41, x=20.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - КОШКА
или МЫШКА
- устойчивее к действию этой программы?
Зашифруйте открытый текст УВЕРОВАТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425, 663), значения случайных чисел для букв открытого текста k: 6, 14, 5, 7, 12, 11, 4, 9, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 5431. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 39, значения цифровой подписи: r = 50; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8832. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 31, значения цифровой подписи: r = 47; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (224, 158), (11, 133) для сообщения с известным значением хэш-свертки 63 и открытым ключом проверки (110,50). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101001101101010111011101.
, построить контрольную сумму для сообщения 1101001101101010111011101.
Зашифровать открытый текст "ЗАПЕЧАТАЙ_ПЕРЕД_ОТПРАВКОЙ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 31452. Величины сдвигов:
позиций в алфавите. Порядок столбцов 31452. Величины сдвигов:  ,
, 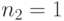 ,
,  ,
,  ,
, 
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=24 и k=5 системы цифровой подписи и подписываемый текст РОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ДЕНЬГИ.
Расшифровать сообщение на английском языке 6-4.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Расшифровать сообщение 5-14.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Вычислить динамическое расстояние порядка (2,2) блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью  бит
бит
Два пользователя используют общий модуль N = 4399, но разные взаимно простые экспоненты 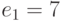 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты 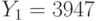 и
и 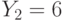 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=28 и k=7 системы цифровой подписи и подписываемый текст ОВАЛ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Шифртекст (671410783, 10111110100000010011) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99439, q=98327. Найти открытый текст и введите его заглавными буквами.
Расшифровать текст 3-13.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Применением цепных дробей найти секретный ключ d и разложение модуля 95841214023781 (экспонента - 2005229) на множители. В ответе укажите секретный ключ.
Шифротекст УПК_ИАКМРАНЫОХ_ЕБЛИ_СО_ЬЛ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Шифротекст ТОЮКЛИЧ_ТЕТОЕ_СИТО_МИНРТО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ИМНЕ_ЯВСТ_СОБЩО_РЕМВРЧИ_Е, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-3.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-19.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение 5-6.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-17.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Зашифровать открытый текст "НЕ_ПОПАДИСЬ_НА_СПИСЫВАНИИ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 54123. Величины сдвигов:
позиций в алфавите. Порядок столбцов 54123. Величины сдвигов: 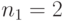 ,
, 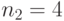 ,
,  ,
,  ,
, 
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст НЕПТУН.
Вычислить динамическое расстояние порядка (2,2) блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста D352 FEAC D98D AC8E шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4559, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 946 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 323 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 321.
Даны значения модуля шифрования N = 3713 и открытого ключа e = 3359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 117, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Два пользователя используют общий модуль N = 4183, но разные взаимно простые экспоненты 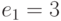 и
и 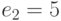 . Пользователи получили шифртексты
. Пользователи получили шифртексты 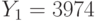 и
и 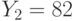 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Три пользователя имеют модули 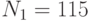 ,
, 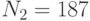 ,
, 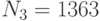 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 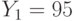 ,
, 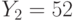 ,
, 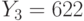 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 762 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {3,6,11,21,43,85,171}, m=343 и n=43. В ответе укажите исходное сообщение.
Шифртекст (5978393092, 10001100110111000010) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92779, q=90127. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (294, 595)}; {(188, 93), (13, 617)}; |
| {(188, 93), (206, 106)}; {(188, 93), (67, 667)}; |
| {(56, 419), (350, 184)}; {(440, 539), (275, 456)}; |
| {(745, 210), (301, 17)}; {(346, 242), (588, 707)}; |
| {(188, 93), (256, 121)}; {(425, 663), (209, 82)}; |
| {(16, 416), (687, 660)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=55 и k=19 системы цифровой подписи и подписываемый текст РУЛЬ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=18 и k=37 системы цифровой подписи и подписываемый текст СХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 146 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=8 и k=35 системы цифровой подписи и подписываемый текст МЕЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Даны значения модуля шифрования N = 319 и открытого ключа e = 33. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 198.
Применением цепных дробей найти секретный ключ d и разложение модуля 89318473363897 (экспонента - 2227661) на множители. В ответе укажите секретный ключ.
Три пользователя имеют модули 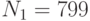 ,
, 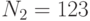 ,
, 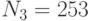 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 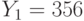 ,
, 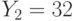 ,
,  . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=9 и k=25 системы цифровой подписи и подписываемый текст ХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Два пользователя используют общий модуль N = 3293, но разные взаимно простые экспоненты 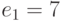 и
и 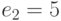 . Пользователи получили шифртексты
. Пользователи получили шифртексты 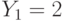 и
и  , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Сообщение 553 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {4,7,12,25,49,98,197}, m=395 и n=61. В ответе укажите исходное сообщение.
Расшифровать сообщение 5-9.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Шифротекст ИРЕМЗЬО_ЕТСНВОНУАЧ_ЮСУТОТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Два пользователя используют общий модуль N = 2419, но разные взаимно простые экспоненты 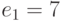 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 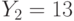 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 173.
Применением цепных дробей найти секретный ключ d и разложение модуля 74701165267919 (экспонента - 3145553) на множители. В ответе укажите секретный ключ.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (128, 672)}; {(56, 419), (59, 386)}; |
| {(425, 663), (106, 24)}; {(568, 355), (145, 608)}; |
| {(188, 93), (279, 398)}; {(425, 663), (99, 295)}; |
| {(179, 275), (269, 187)}; {(188, 93), (395, 337)}; |
| {(188, 93), (311, 68)}; {(135, 82), (556, 484)}; |
| {(56, 419), (106, 727)}; {(16, 416), (307, 693)} |
Провести первый раунд зашифрования открытого текста D12F 992B B2AD C9BA шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7256. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 51, значения цифровой подписи: r = 41; s = 44. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Шифртекст (7764435203, 10010100111100010011) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93151, q=94483. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст 86, а также значения модуля шифрования N = 323 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить действительность подписей (106, 108), (35, 44) для сообщения с известным значением хэш-свертки 166 и открытым ключом проверки (436,660). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИКЕТ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=37, x=10.
Чей компьютер он взломает быстрее?
Три пользователя имеют модули 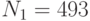 ,
, 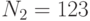 ,
, 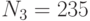 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 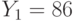 ,
, 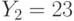 ,
, 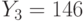 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111001110011000110000001.
, построить контрольную сумму для сообщения 1111001110011000110000001.
Шифротекст УЛОЧПЛЭ_ЕИОРТНК_ЮУПНУТЧ_О получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ИРТЙООИИЛББ__ОД_ТИКЕПК_КА, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-8.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение 4-6.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение 5-5.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Зашифровать открытый текст "ВОДИТЕЛЬ_НЕ_ПОДНИМАЙ_ПЫЛЬ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 32541. Величины сдвигов:
позиций в алфавите. Порядок столбцов 32541. Величины сдвигов: 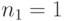 ,
, 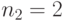 ,
,  ,
,  ,
, 
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРЯМАЯ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=31, x=7.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - МЯЧИК
или ШАРИК
- устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка (2,2) блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста 8966 FB62 A4AA FAD9 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 3149, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 2027 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 261.
Даны значения модуля шифрования N = 5723 и открытого ключа e = 301. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 72903890242273 (экспонента - 3261683) на множители. В ответе укажите секретный ключ.
Дан шифртекст 311, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Два пользователя используют общий модуль N = 3149, но разные взаимно простые экспоненты 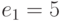 и
и 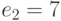 . Пользователи получили шифртексты
. Пользователи получили шифртексты 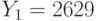 и
и 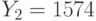 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Три пользователя имеют модули  ,
,  ,
, 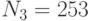 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 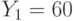 ,
, 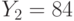 ,
, 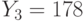 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 561 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,6,8,17,35,69,137}, m=275 и n=107. В ответе укажите исходное сообщение.
Шифртекст (3466465879, 01111000011000111101) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99023, q=92479. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст НИЗМЕННЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 12, 5, 7, 17, 18, 2, 12, 10, 11, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (623, 166)}; {(725, 195), (513, 414)}; |
| {(346, 242), (461, 4)}; {(489, 468), (739, 574)}; |
| {(725, 195), (663, 476)}; {(745, 210), (724, 522)}; |
| {(725, 195), (663, 476)}; {(618, 206), (438, 40)}; |
| {(286, 136), (546, 670)}; {(179, 275), (73, 72)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=19 и k=37 системы цифровой подписи и подписываемый текст ВОСК. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=52 и k=41 системы цифровой подписи и подписываемый текст ГОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7327. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 42; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=3. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=2, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (3, 7) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (31, 171), (211,141) для сообщения с известным значением хэш-свертки 182 и открытым ключом проверки (239,329). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=7 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 80.
Сообщение 305 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,2,6,10,21,41,85}, m=167 и n=48. В ответе укажите исходное сообщение.
Два пользователя используют общий модуль N = 5561, но разные взаимно простые экспоненты 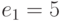 и
и 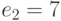 . Пользователи получили шифртексты
. Пользователи получили шифртексты 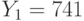 и
и 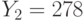 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Зашифровать открытый текст "ПРИНИМАТЬ_ПО_ДВЕ_ТАБЛЕТКИ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 45213. Величины сдвигов:
позиций в алфавите. Порядок столбцов 45213. Величины сдвигов: 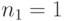 ,
, 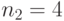 ,
,  ,
,  ,
, 
Дано: модуль шифрования N = 2491, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 388 на открытом ключе (N, e) по алгоритму RSA.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МИНУТА.
Два пользователя используют общий модуль N = 3403, но разные взаимно простые экспоненты 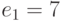 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 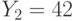 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Провести первый раунд зашифрования открытого текста BDD3 AE17 C12A F70A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Расшифровать сообщение на английском языке 6-13.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Зашифровать открытый текст "КРИПТОАНАЛИЗ_ОЧЕНЬ_СЛОЖЕН". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 51324. Величины сдвигов:
позиций в алфавите. Порядок столбцов 51324. Величины сдвигов: 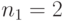 ,
, 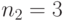 ,
,  ,
,  ,
, 
Зашифруйте открытый текст ОТСЛУЖИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(16, 416), значения случайных чисел для букв открытого текста k: 2, 8, 4, 2, 6, 10, 3, 3, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(377, 456), (367, 360)}; {(425, 663), (715, 398)}; |
| {(188, 93), (279, 353)}; {(179, 275), (128, 79)}; |
| {(568, 355), (515, 67)}; {(568, 355), (482, 230)}; |
| {(377, 456), (206, 645)}; {(188, 93), (300, 455)}; |
| {(489, 468), (362, 446)}; {(16, 416), (69, 510)}; |
| {(425, 663), (218, 601)} |
Расшифровать сообщение 5-7.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Шифротекст РВЕПИИЕ_ДТРМЕПИ_ИАРДРМЫГА получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Сообщение 180 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,5,8,16,34,67,136}, m=270 и n=139. В ответе укажите исходное сообщение.
Проверить действительность подписей (71, 65), (127, 230) для сообщения с известным значением хэш-свертки 52 и открытым ключом проверки (10,275). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Даны значения модуля шифрования N = 4183 и открытого ключа e = 519. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка (2,2) блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью  бит
бит
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=15 и k=17 системы цифровой подписи и подписываемый текст КОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст УРАГАН.
Проверьте подлинность ЭЦП (7, 4) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Два пользователя используют общий модуль N = 5293, но разные взаимно простые экспоненты 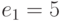 и
и 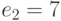 . Пользователи получили шифртексты
. Пользователи получили шифртексты 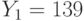 и
и  , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=4 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Шифртекст (8611143873, 01001110000001100000) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98207, q=90679. Найти открытый текст и введите его заглавными буквами.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ОКОШКО
или ДВЕРЦА
- устойчивее к действию этой программы?
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2764. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 8, значения цифровой подписи: r = 47; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать сообщение на английском языке 6-7.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=37, x=11.
Чей компьютер он взломает быстрее?
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 87.
Проверить действительность подписей (3, 85), (195, 216) для сообщения с известным значением хэш-свертки 215 и открытым ключом проверки (104,30). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать фразу ИПССАДП_ЕРЕЕДИНЖПУЕРАОБЗ_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Проверьте подлинность ЭЦП (7, 10) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Расшифровать сообщение 5-17.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Провести первый раунд зашифрования открытого текста AC2B EECD DA96 989D шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Сообщение 1309 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {4,6,11,22,45,90,181}, m=360 и n=79. В ответе укажите исходное сообщение.
Шифртекст (978847044, 10011100011011001101) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99971, q=98143. Найти открытый текст и введите его заглавными буквами.
Расшифровать сообщение 4-18.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1746. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 47, значения цифровой подписи: r = 31; s = 56. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=12, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Два пользователя используют общий модуль N = 3953, но разные взаимно простые экспоненты 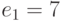 и
и 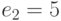 . Пользователи получили шифртексты
. Пользователи получили шифртексты 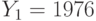 и
и 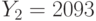 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Дан шифртекст 75, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8806. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 29, значения цифровой подписи: r = 50; s = 24. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (11, 133), (35, 48) для сообщения с известным значением хэш-свертки 148 и открытым ключом проверки (166,741). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(56, 419), (739, 177)}; {(16, 416), (282, 410)}; |
| {(425, 663), (221, 138)}; {(188, 93), (329, 447)}; |
| {(286, 136), (235, 19)}; {(725, 195), (496, 31)}; |
| {(56, 419), (236, 712)}; {(440, 539), (514, 662)}; |
| {(377, 456), (323, 94)}; {(179, 275), (203, 324)}; |
| {(568, 355), (197, 606)} |
Сообщение 212 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,2,4,8,17,34,68}, m=135 и n=103. В ответе укажите исходное сообщение.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 285.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=11 и k=55 системы цифровой подписи и подписываемый текст СЛОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Применением цепных дробей найти секретный ключ d и разложение модуля 84032429242009 (экспонента - 2581907) на множители. В ответе укажите секретный ключ.
Шифротекст ЮВЧКЛ_ИКТЕЬОЮМП_ТВЕРТ_ЬСЕ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Провести первый раунд зашифрования открытого текста BDC6 FF70 AC32 B3A6 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить динамическое расстояние порядка (2,2) блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью  бит
бит
Два пользователя используют общий модуль N = 2701, но разные взаимно простые экспоненты 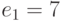 и
и 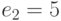 . Пользователи получили шифртексты
. Пользователи получили шифртексты 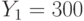 и
и 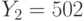 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Расшифровать сообщение 5-16.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-22.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Расшифровать сообщение 4-20.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=13 и k=23 системы цифровой подписи и подписываемый текст ТРЕП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Применением цепных дробей найти секретный ключ d и разложение модуля 77027476849549 (экспонента - 2936957) на множители. В ответе укажите секретный ключ.
Даны значения модуля шифрования N = 221 и открытого ключа e = 91. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 79.
Расшифровать фразу ВЕОИТ_ЛЕФИСНУТАНЫ_ОВТ_ЬРЫ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Два пользователя используют общий модуль N = 4307, но разные взаимно простые экспоненты 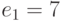 и
и 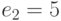 . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 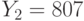 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Расшифровать сообщение 4-16.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ПРОБИРКА
или МЕНЗУРКА
- устойчивее к действию этой программы?
Проверить действительность подписей (3, 220), (10, 171) для сообщения с известным значением хэш-свертки 152 и открытым ключом проверки (195, 321). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать текст 3-20.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Расшифровать сообщение на английском языке 6-18.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Дан шифртекст 47, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Провести первый раунд зашифрования открытого текста 97F4 C6AD D65F A8A2 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ТОВАР
или РЫНОК
- устойчивее к действию этой программы?
Шифртекст (438845908, 10101000101000000100) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93131, q=90247. Найти открытый текст и введите его заглавными буквами.
Даны значения модуля шифрования N = 253 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 106.
Проверьте подлинность ЭЦП (5, 11) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Три пользователя имеют модули 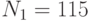 ,
, 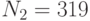 ,
, 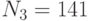 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 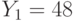 ,
, 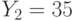 ,
, 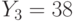 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Провести первый раунд зашифрования открытого текста BF55 E71E 8CD6 9001 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Шифротекст СИЫЧВТ_ИЛЛЕОЧНООЛПО_ЕИЕНЖ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу А__ФНРЕПДЕТЕА_ЙРУВСИШКЛЕЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8190. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 10, значения цифровой подписи: r = 56; s = 48. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сообщение 557 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {3,5,9,19,37,77,151}, m=302 и n=59. В ответе укажите исходное сообщение.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=23, x=17.
Чей компьютер он взломает быстрее?
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Два пользователя используют общий модуль N = 3431, но разные взаимно простые экспоненты 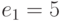 и
и 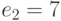 . Пользователи получили шифртексты
. Пользователи получили шифртексты 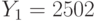 и
и 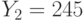 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью  бит
бит
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (326, 675)}; {(725, 195), (83, 378)}; |
| {(440, 539), (340, 78)}; {(425, 663), (67, 84)}; |
| {(425, 663), (620, 71)}; {(72, 254), (251, 245)}; |
| {(568, 355), (75, 318)}; {(725, 195), (228, 271)}; |
| {(188, 93), (734, 170)}; {(188, 93), (704, 705)}; |
| {(286, 136), (235, 732)} |
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст САТУРН.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111111111010001011001100.
, построить контрольную сумму для сообщения 1111111111010001011001100.
Зашифруйте открытый текст РЕМОНТНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 2, 2, 4, 18, 15, 19, 11, 2, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить действительность подписей (3, 208), (166, 235) для сообщения с известным значением хэш-свертки 14 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - КРЫСА
или ХОРЕК
- устойчивее к действию этой программы?
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1892. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 37, значения цифровой подписи: r = 56; s = 26. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Провести первый раунд зашифрования открытого текста A267 8C95 8111 B0B7 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4331, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 632 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2455. Используя метод факторизации Ферма, найти значение закрытого ключа.
Расшифровать сообщение 5-20.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Шифротекст ЫТБСРЕПЕ_ОВДДОИЕВТ_ОСАЙК_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-5.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-11.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.Вычислить динамическое расстояние порядка (2,2) блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Дано: модуль шифрования N = 3403, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 855 на открытом ключе (N, e) по алгоритму RSA.
Дан шифртекст 96, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 295 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,5,8,16,31,63,125}, m=251 и n=56. В ответе укажите исходное сообщение.
Шифртекст (942315396, 10100111100011100111) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100019, q=94903. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (573, 583)}; {(188, 93), (128, 79)}; |
| {(425, 663), (703, 125)}; {(489, 468), (109, 200)}; |
| {(568, 355), (348, 27)}; {(377, 456), (323, 657)}; |
| {(72, 254), (399, 65)}; {(16, 416), (660, 275)}; |
| {(179, 275), (267, 670)}; {(568, 355), (642, 53)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=5 и k=31 системы цифровой подписи и подписываемый текст ШАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (712, 186)}; {(725, 195), (395, 414)}; |
| {(72, 254), (434, 136)}; {(425, 663), (251, 506)}; |
| {(16, 416), (383, 340)}; {(745, 210), (102, 484)}; |
| {(346, 242), (78, 271)}; {(179, 275), (712, 186)}; |
| {(725, 195), (739, 574)}; {(346, 242), (78, 271)} |
Вычислить динамическое расстояние порядка (2,2) блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью  бит
бит
Сообщение 855 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {4,5,11,21,43,85,170}, m=340 и n=101. В ответе укажите исходное сообщение.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=7, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Зашифровать открытый текст "ГОТОВЬТЕСЬ_СДАВАТЬ_ЗАЧЁТЫ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 25314. Величины сдвигов:
позиций в алфавите. Порядок столбцов 25314. Величины сдвигов:  ,
, 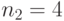 ,
,  ,
,  ,
, 
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=23, x=9.
Чей компьютер он взломает быстрее?
Проверить действительность подписей (201, 7), (195, 143) для сообщения с известным значением хэш-свертки 20 и открытым ключом проверки (87,716). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Даны значения модуля шифрования N = 3901 и открытого ключа e = 2375. Используя метод факторизации Ферма, найти значение закрытого ключа.
Расшифровать сообщение 5-8.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Дано: модуль шифрования N = 1739, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 132 на открытом ключе (N, e) по алгоритму RSA.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=47, x=12.
Чей компьютер он взломает быстрее?
Провести первый раунд зашифрования открытого текста F7C1 A026 AB48 9F0F шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Зашифровать открытый текст "ВНИМАНИЕ_ВСЕМ_СОТРУДНИКАМ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 42315. Величины сдвигов:
позиций в алфавите. Порядок столбцов 42315. Величины сдвигов: 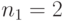 ,
, 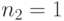 ,
,  ,
,  ,
, 
Зашифруйте открытый текст ПРОКРУТКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(618, 206), значения случайных чисел для букв открытого текста k: 10, 15, 16, 2, 3, 4, 2, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Два пользователя используют общий модуль N = 1927, но разные взаимно простые экспоненты 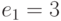 и
и 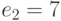 . Пользователи получили шифртексты
. Пользователи получили шифртексты 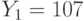 и
и 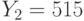 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1571. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью  бит
бит
Расшифровать текст 3-15.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Шифротекст АМО_ЛЕРУРСОС_ДВЯЛЗА_УПКАС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ТСАНУОБЛЬ_ИВТЕО_ЕРОШТЕОКЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-13.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-14.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПОБЕДА.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=47, x=13.
Чей компьютер он взломает быстрее?
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста A7BE CFBC F166 AB89 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 2923, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 678 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 4717 и открытого ключа e = 4205. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 60902079700513 (экспонента - 3914857) на множители. В ответе укажите секретный ключ.
Дан шифртекст 45, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Три пользователя имеют модули 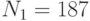 ,
,  ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 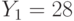 ,
, 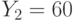 ,
, 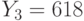 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(283, 493), (314, 127)}; {(425, 663), (561, 140)}; |
| {(568, 355), (75, 433)}; {(440, 539), (602, 627)}; |
| {(188, 93), (395, 414)}; {(179, 275), (25, 604)}; |
| {(72, 254), (47, 349)}; {(72, 254), (417, 137)}; |
| {(188, 93), (298, 225)}; {(56, 419), (79, 111)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=25 и k=17 системы цифровой подписи и подписываемый текст СТОП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=21 и k=5 системы цифровой подписи и подписываемый текст ГИД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (195, 216), (9, 85) для сообщения с известным значением хэш-свертки 7 и открытым ключом проверки (245,637). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать фразу ЕМОТНББСУОЙИТН_СЙРЕ_СТЯЕЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2929. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 78908333904637 (экспонента - 2821057) на множители. В ответе укажите секретный ключ.
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (455, 383). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=6 и k=29 системы цифровой подписи и подписываемый текст БАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Шифротекст САЕДЛТА_ЬЗМ_НЕУПМРЕЕЕЙННО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=4 и k=41 системы цифровой подписи и подписываемый текст ШУМ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3057. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 58, значения цифровой подписи: r = 11; s = 2. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Провести первый раунд зашифрования открытого текста CBD9 93EC CB0F F839 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ПРОСТУДА
или СКВОЗНЯК
- устойчивее к действию этой программы?
Дано: модуль шифрования N = 5561, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 2718 на открытом ключе (N, e) по алгоритму RSA.
Вычислить динамическое расстояние порядка (2,2) блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью  бит
бит
Расшифровать фразу НУАСТРИОДЕРРОАТТЕСГИВО_ВИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101101110110010110101.
, построить контрольную сумму для сообщения 1110101101110110010110101.
Шифротекст РОВПЕ_ИТНЕЛЕГРУ_ТОЯРОЛЕВВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать сообщение 4-3.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-11.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Зашифровать открытый текст "ЗАКРЫТЫЙ_КЛЮЧ_НЕ_РАЗДАВАЙ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 43215. Величины сдвигов:
позиций в алфавите. Порядок столбцов 43215. Величины сдвигов: 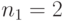 ,
, 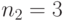 ,
,  ,
,  ,
, 
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРОРЫВ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=43, x=7.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ДОКЛАД
или ТЕЗИСЫ
- устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка (2,2) блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста C95A B90A 8B3D EB0 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 1927, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 1260 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 187 и открытого ключа e = 59. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 114.
Даны значения модуля шифрования N = 2479 и открытого ключа e = 2251. Используя метод факторизации Ферма, найти значение закрытого ключа.
Три пользователя имеют модули 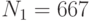 ,
,  ,
, 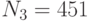 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов  ,
,  ,
,  . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Зашифруйте открытый текст БЕЛИБЕРДА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 2, 9, 18, 2, 19, 4, 5, 11, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (150, 355)}; {(188, 93), (394, 20)}; |
| {(725, 195), (13, 134)}; {(377, 456), (209, 669)}; |
| {(56, 419), (514, 662)}; {(56, 419), (243, 87)}; |
| {(618, 206), (719, 538)}; {(618, 206), (159, 13)}; |
| {(618, 206), (326, 76)}; {(188, 93), (557, 28)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6549. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 11, значения цифровой подписи: r = 38; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (7, 8) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (166, 242), (3, 9) для сообщения с известным значением хэш-свертки 84 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=37, x=5.
Чей компьютер он взломает быстрее?
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЮПИТЕР.
Шифротекст ЫОЧНТО_КОЕАДИНР_Ы_ВТЕУПЛД получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Зашифруйте открытый текст СИММЕТРИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 11, 17, 18, 19, 16, 6, 12, 8, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст 64, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Даны значения модуля шифрования N = 2911 и открытого ключа e = 1697. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дано: модуль шифрования N = 5609, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4425 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=44 и k=11 системы цифровой подписи и подписываемый текст СВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Расшифровать фразу К_ЙАО__ЕУНОМЕПЧН_ЮЗАТТ_КО, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (273, 481)}; {(188, 93), (85, 716)}; |
| {(16, 416), (422, 162)}; {(283, 493), (36, 87)}; |
| {(179, 275), (100, 364)}; {(188, 93), (298, 225)}; |
| {(56, 419), (555, 303)}; {(745, 210), (100, 387)}; |
| {(377, 456), (526, 412)}; {(286, 136), (316, 228)}; |
| {(745, 210), (49, 183)}; {(179, 275), (428, 247)} |
Дан шифртекст 163, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2563. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 33, значения цифровой подписи: r = 11; s = 34. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Применением цепных дробей найти секретный ключ d и разложение модуля 70109121369029 (экспонента - 3401467) на множители. В ответе укажите секретный ключ.
Проверьте подлинность ЭЦП (11, 9) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗБОР.
Зашифруйте открытый текст РЕНЕССАНС с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 2, 19, 4, 8, 2, 2, 16, 10, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Три пользователя имеют модули 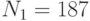 ,
, 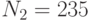 ,
, 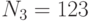 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 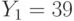 ,
, 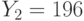 ,
, 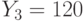 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111111100000111001000110.
, построить контрольную сумму для сообщения 1111111100000111001000110.
Шифротекст ША_УНППРААУТУРААЗЕМ_ЛИ_ИТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу _ААЛВРАТЗВД_УАББТОЕ__ЕИБГ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-5.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение 5-18.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-24.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Зашифровать открытый текст "КРИПТОГРАФИЯ_ВАЖНАЯ_НАУКА". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 52314. Величины сдвигов:
позиций в алфавите. Порядок столбцов 52314. Величины сдвигов:  ,
, 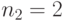 ,
,  ,
,  ,
, 
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ТАЙМЕР
или ЗВОНОК
- устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста B05F A79E CEF6 AA22 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 3397 и открытого ключа e = 113. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 47050437355283 (экспонента - 4674517) на множители. В ответе укажите секретный ключ.
Дан шифртекст 13, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Два пользователя используют общий модуль N = 4891, но разные взаимно простые экспоненты 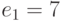 и
и 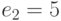 . Пользователи получили шифртексты
. Пользователи получили шифртексты 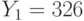 и
и 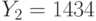 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Три пользователя имеют модули  ,
, 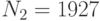 ,
, 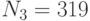 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 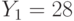 ,
, 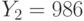 ,
, 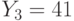 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 1018 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {5,6,13,25,54,107,211}, m=423 и n=167. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ТЕРНОВНИК с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 8, 14, 17, 17, 2, 10, 8, 2, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (259, 401)}; {(568, 355), (606, 147)}; |
| {(188, 93), (407, 82)}; {(56, 419), (739, 574)}; |
| {(286, 136), (329, 447)}; {(425, 663), (520, 749)}; |
| {(72, 254), (374, 315)}; {(188, 93), (149, 97)}; |
| {(745, 210), (13, 134)}; {(440, 539), (235, 19)}; |
| {(425, 663), (128, 79)} |
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (3, 49), (3, 85) для сообщения с известным значением хэш-свертки 31 и открытым ключом проверки (318,109). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Сообщение 782 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {4,5,10,21,45,88,174}, m=349 и n=80. В ответе укажите исходное сообщение.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=31, x=12.
Чей компьютер он взломает быстрее?
Расшифровать текст 3-17.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Три пользователя имеют модули  ,
,  ,
, 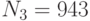 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 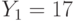 ,
, 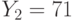 ,
, 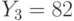 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Проверьте подлинность ЭЦП (7, 5) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Зашифруйте открытый текст МУШТРОВКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(618, 206), значения случайных чисел для букв открытого текста k: 5, 19, 8, 2, 5, 8, 15, 19, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=47, x=16.
Чей компьютер он взломает быстрее?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101100010111101110010.
, построить контрольную сумму для сообщения 1110101100010111101110010.
Расшифровать сообщение на английском языке 6-15.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Найти число всех подгрупп (не включая единичную) группы 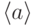 порядка 5202, не содержащих элемент порядка 18.
порядка 5202, не содержащих элемент порядка 18.
Расшифровать текст 3-7.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье с конца слово заглавными буквами.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Дано: модуль шифрования N = 3713, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 3415 на открытом ключе (N, e) по алгоритму RSA.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ДОЛЛАР
или ФАНТИК
- устойчивее к действию этой программы?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100001010011100001100010.
, построить контрольную сумму для сообщения 1100001010011100001100010.
Расшифровать текст 3-16.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-1.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАКЕТА.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=47, x=8.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ЗРНТИК
или ДОЖДИК
- устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка (2,2) блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью  бит
бит
Провести первый раунд зашифрования открытого текста A64E D30C E720 E3E8 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 6319, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2741 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 386.
Два пользователя используют общий модуль N = 2773, но разные взаимно простые экспоненты 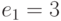 и
и 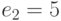 . Пользователи получили шифртексты
. Пользователи получили шифртексты 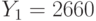 и
и 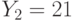 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Три пользователя имеют модули 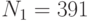 ,
,  ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 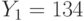 ,
, 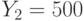 ,
, 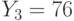 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Шифртекст (9775365428, 11010000001111001000) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101987, q=101267. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (651, 560)}; {(425, 663), (147, 361)}; |
| {(286, 136), (109, 551)}; {(440, 539), (90, 730)}; |
| {(618, 206), (668, 342)}; {(745, 210), (109, 200)}; |
| {(425, 663), (147, 361)}; {(72, 254), (228, 480)}; |
| {(346, 242), (530, 22)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=10 и k=35 системы цифровой подписи и подписываемый текст БОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (127, 230), (71, 65) для сообщения с известным значением хэш-свертки 165 и открытым ключом проверки (624,469). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2205. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 27, значения цифровой подписи: r = 13; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Дан шифртекст 185, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 172.
Дано: модуль шифрования N = 4891, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4654 на открытом ключе (N, e) по алгоритму RSA.
Шифротекст КАЛЗААК_ДЗИШТАА_ВЯ_Д_ООРС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью  бит
бит
Два пользователя используют общий модуль N = 5723, но разные взаимно простые экспоненты 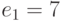 и
и 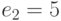 . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 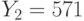 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Дан шифртекст 96, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 4-4.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.Три пользователя имеют модули 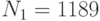 ,
, 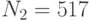 ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 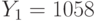 ,
, 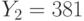 ,
, 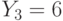 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Расшифровать фразу АЗАДЙАЧЬЛНОЛИВЯЕЫУ_СЕТН_А, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-22.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение 4-17.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение 5-2.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Вычислить динамическое расстояние порядка (2,2) блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью  бит
бит
Даны значения модуля шифрования N = 299 и открытого ключа e = 61. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 178.
Применением цепных дробей найти секретный ключ d и разложение модуля 81177745546021 (экспонента - 2711039) на множители. В ответе укажите секретный ключ.
Дан шифртекст 58, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 480 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,6,9,19,38,75,151}, m=301 и n=113. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ОТСЛЕДИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 19, 2, 13, 5, 19, 5, 7, 8, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (93, 484)}; {(489, 468), (531, 397)}; |
| {(188, 93), (654, 102)}; {(489, 468), (218, 150)}; |
| {(16, 416), (530, 729)}; {(425, 663), (295, 219)}; |
| {(725, 195), (742, 299)}; {(188, 93), (367, 360)}; |
| {(188, 93), (235, 732)}; {(618, 206), (251, 245)}; |
| {(425, 663), (688, 10)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1989. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 42, значения цифровой подписи: r = 34; s = 13. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 4381. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 32, значения цифровой подписи: r = 24; s = 45. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7144. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 22, значения цифровой подписи: r = 47; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью  бит
бит
Даны значения модуля шифрования N = 3403 и открытого ключа e = 2439. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 152, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 5-15.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Дано: модуль шифрования N = 5063, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 4679 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 493 и открытого ключа e = 369. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 300.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст пробел.
Расшифровать сообщение 4-7.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (724, 522)}; {(489, 468), (719, 538)}; |
| {(56, 419), (205, 372)}; {(72, 254), (628, 293)}; |
| {(188, 93), (594, 337)}; {(440, 539), (588, 707)}; |
| {(568, 355), (707, 556)}; {(489, 468), (719, 538)}; |
| {(16, 416), (590, 376)}; {(56, 419), (612, 329)}; |
| {(188, 93), (594, 337)} |
Вычислить динамическое расстояние порядка (2,2) блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью  бит
бит
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=41, x=7.
Чей компьютер он взломает быстрее?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1011110100111110001011011.
, построить контрольную сумму для сообщения 1011110100111110001011011.
Даны значения модуля шифрования N = 3569 и открытого ключа e = 265. Используя метод факторизации Ферма, найти значение закрытого ключа.
Расшифровать фразу РСГЕИЯ_Н_ЕТИАРЦСОСОТИ_СТЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Дан шифртекст 28, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать текст 3-23.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Расшифровать сообщение 4-14.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение 5-10.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-23.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ВОЛК
или ЗАЯЦ
- устойчивее к действию этой программы?
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 209 и открытого ключа e = 53. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 85.
Даны значения модуля шифрования N = 4183 и открытого ключа e = 2099. Используя метод факторизации Ферма, найти значение закрытого ключа.
Два пользователя используют общий модуль N = 5251, но разные взаимно простые экспоненты 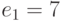 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 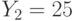 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Зашифруйте открытый текст ПРОКОПАТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 3, 16, 17, 5, 16, 18, 3, 7, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (426, 662)}; {(72, 254), (67, 667)}; |
| {(286, 136), (739, 574)}; {(16, 416), (143, 602)}; |
| {(618, 206), (313, 203)}; {(618, 206), (114, 607)}; |
| {(618, 206), (438, 711)}; {(188, 93), (573, 168)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3629. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 54, значения цифровой подписи: r = 56; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=4, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (7, 7) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=47, n2=41, x=9.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст НИКЕЛЕВЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=,(568, 355) значения случайных чисел для букв открытого текста k: 9, 9, 2, 3, 8, 19, 6, 18, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Шифротекст ПКЕРЕЛТИЧЮЕМУТ_Б_РЕЛВХРЕВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Зашифровать открытый текст "ЗДЕСЬ_ДН.М_БУДУТ_ЭКЗАМЕНЫ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 31425. Величины сдвигов:
позиций в алфавите. Порядок столбцов 31425. Величины сдвигов: 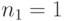 ,
, 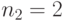 ,
,  ,
,  ,
, 
Проверить действительность подписей (10, 163), (10, 153) для сообщения с известным значением хэш-свертки 169 и открытым ключом проверки (671,267). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Провести первый раунд зашифрования открытого текста F1FE EF23 8B38 B3BF шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ГОРШОК
или ЦВЕТОК
- устойчивее к действию этой программы?
Расшифровать сообщение 5-4.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Зашифровать открытый текст "ЖИЗНЬ_СТУДЕНТА_ВНЕ_УГРОЗЫ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 42153. Величины сдвигов:
позиций в алфавите. Порядок столбцов 42153. Величины сдвигов:  ,
, 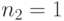 ,
,  ,
,  ,
, 
Расшифровать текст 3-4.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Зашифруйте открытый текст ОТСТУПИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 7, 9, 3, 8, 18, 18, 8, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИВАЯ.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100010010010001001001100.
, построить контрольную сумму для сообщения 1100010010010001001001100.
Расшифровать фразу П_КИУУТОРГ.ЙЕ_Щ_О_КИАУЛСБ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-18.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-8.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Зашифровать открытый текст "ПОЛОЖИТЕ_ДИСКИ_ПОД_КАМЕНЬ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 31542. Величины сдвигов:
позиций в алфавите. Порядок столбцов 31542. Величины сдвигов:  ,
, 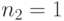 ,
,  ,
,  ,
, 
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МАСТЕР.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 437 и открытого ключа e = 233. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 381.
Даны значения модуля шифрования N = 1891 и открытого ключа e = 277. Используя метод факторизации Ферма, найти значение закрытого ключа.
Три пользователя имеют модули 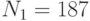 ,
, 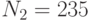 ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 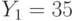 ,
, 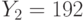 ,
,  . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 302 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,4,6,12,25,49,100}, m=199 и n=78. В ответе укажите исходное сообщение.
Зашифруйте открытый текст МЫСЛЕННЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(346, 242), значения случайных чисел для букв открытого текста k: 6, 17, 18, 11, 18, 2, 4, 2, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3271. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 21, значения цифровой подписи: r = 2; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Даны значения модуля шифрования N = 143 и открытого ключа e = 19. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 115.
Провести первый раунд зашифрования открытого текста E90A F652 CD88 F9EC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=33 и k=35 системы цифровой подписи и подписываемый текст СКАЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Зашифровать открытый текст "БИЛЕТЫ_ЛЕЖАТ_ПОД_ЖУРНАЛОМ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 25341. Величины сдвигов:
позиций в алфавите. Порядок столбцов 25341. Величины сдвигов:  ,
, 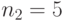 ,
,  ,
,  ,
, 
Применением цепных дробей найти секретный ключ d и разложение модуля 54296750879837 (экспонента - 4282063) на множители. В ответе укажите секретный ключ.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста C20A 8A8E A533 C2AB шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Даны значения модуля шифрования N = 3239 и открытого ключа e = 2467. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8948. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 30, значения цифровой подписи: r = 38; s = 16. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Найти число всех подгрупп (не включая единичную) группы 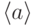 порядка 5545, не содержащих элемент порядка 5.
порядка 5545, не содержащих элемент порядка 5.
Шифртекст (3928629409, 01011110010001001001) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=96263, q=98479. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (185, 105)}; {(188, 93), (681, 385)}; |
| {(377, 456), (576, 465)}; {(440, 539), (138, 298)}; |
| {(745, 210), (520, 2)}; {(188, 93), (681, 385)}; |
| {(286, 136), (282, 410)}; {(72, 254), (200, 721)}; |
| {(72, 254), (643, 94)}; {(745, 210), (476, 315)}; |
| {(440, 539), (724, 229)} |
Расшифровать текст 3-9.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-1.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Вычислить динамическое расстояние порядка (2,2) блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью  бит
бит
Провести первый раунд зашифрования открытого текста C485 FB04 B366 E288 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 59046883376179 (экспонента - 4044583) на множители. В ответе укажите секретный ключ.
Три пользователя имеют модули  ,
, 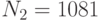 ,
, 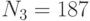 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 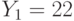 ,
, 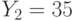 ,
, 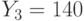 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Шифртекст (8978530064, 11010000110111010111) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95747, q=95327. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст ТЕРПЕЛИВО с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 17, 5, 4, 17, 13, 2, 17, 14, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (99, 456)}; {(425, 663), (31, 136)}; |
| {(377, 456), (688, 741)}; {(425, 663), (636, 747)}; |
| {(16, 416), (298, 526)}; {(188, 93), (356, 175)}; |
| {(489, 468), (147, 390)}; {(346, 242), (546, 670)}; |
| {(72, 254), (114, 144)}; {(377, 456), (25, 147)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1867. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 36; s = 57. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать фразу РЕТИ_АУКС_РКСАРГФАРАРБЗАЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=23, x=19.
Чей компьютер он взломает быстрее?
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=17 и k=11 системы цифровой подписи и подписываемый текст ЩИТ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Зашифруйте открытый текст ОТСТАВНОЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 5, 3, 3, 2, 4, 19, 2, 4, 10, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью  бит
бит
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (269, 564)}; {(179, 275), (73, 72)}; |
| {(440, 539), (189, 454)}; {(618, 206), (628, 458)}; |
| {(568, 355), (660, 275)}; {(72, 254), (709, 595)}; |
| {(745, 210), (12, 314)}; {(188, 93), (36, 664)}; |
| {(618, 206), (530, 22)}; {(286, 136), (532, 50)}; |
| {(425, 663), (660, 275)}; {(725, 195), (482, 230)} |
Дано: модуль шифрования N = 8633, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 688 на открытом ключе (N, e) по алгоритму RSA.
Найти число всех подгрупп (не включая единичную) группы 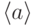 порядка 6656, не содержащих элемент порядка 26.
порядка 6656, не содержащих элемент порядка 26.
Расшифровать сообщение 5-12.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Шифртекст (102131499, 11010111001111111000) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95891, q=90007. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст ИЗЛЕЧИМЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 10, 14, 2, 2, 10, 10, 14, 3, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Расшифровать сообщение на английском языке 6-2.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ВОРОНА
или ЛИСИЦА
- устойчивее к действию этой программы?
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 2911 и открытого ключа e = 487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 13, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Три пользователя имеют модули  ,
,  ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 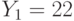 ,
, 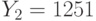 ,
, 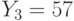 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 812 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {5,6,12,24,48,98,195}, m=389 и n=111. В ответе укажите исходное сообщение.
Шифртекст (5538085341, 11011101111000111001) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=90059, q=91199. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (9, 150)}; {(745, 210), (138, 453)}; |
| {(56, 419), (36, 87)}; {(283, 493), (39, 580)}; |
| {(377, 456), (515, 684)}; {(346, 242), (458, 261)}; |
| {(283, 493), (105, 369)}; {(568, 355), (326, 675)}; |
| {(425, 663), (529, 358)}; {(283, 493), (668, 409)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3669. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 15, значения цифровой подписи: r = 6; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 383). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (150,17), (195, 167) для сообщения с известным значением хэш-свертки 59 и открытым ключом проверки (60,74). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Сообщение 595 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,5,9,17,35,77,146}, m=292 и n=109. В ответе укажите исходное сообщение.
Даны значения модуля шифрования N = 1891 и открытого ключа e = 1487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка (2,2) блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью  бит
бит
Шифротекст ПРГРОА_АММНАЗЕ_ПАКУСЕ_ЯТС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-14.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Дан шифртекст 82, а также значения модуля шифрования N = 119 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Дано: модуль шифрования N = 5767, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 3063 на открытом ключе (N, e) по алгоритму RSA.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Сообщение 442 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,4,8,15,30,60,122}, m=244 и n=83. В ответе укажите исходное сообщение.
Расшифровать сообщение 4-8.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-10.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЧАЙНИК.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ЧАЙНИК
или МАСТЕР
- устойчивее к действию этой программы?
Провести первый раунд зашифрования открытого текста 8DAA 8960 C100 DFD3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 209 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 92.
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1103. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 67510894259489 (экспонента - 3543923) на множители. В ответе укажите секретный ключ.
Три пользователя имеют модули 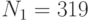 ,
,  ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 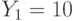 ,
, 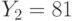 ,
, 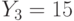 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Шифртекст (8137015367, 01101001111001011111) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98899, q=101531. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст КУПАЛЬЩИК с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 17, 17, 9, 12, 17, 7, 15, 7, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(72, 254), (397, 184)}; {(188, 93), (526, 412)}; |
| {(188, 93), (328, 290)}; {(135, 82), (433, 47)}; |
| {(179, 275), (711, 341)}; {(568, 355), (546, 670)}; |
| {(16, 416), (734, 170)}; {(568, 355), (371, 14)}; |
| {(596, 433), (604, 610)}; {(16, 416), (734, 170)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=12 и k=47 системы цифровой подписи и подписываемый текст ЛУЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Проверьте подлинность ЭЦП (3, 10) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Дано: модуль шифрования N = 1763, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 436 на открытом ключе (N, e) по алгоритму RSA.
Применением цепных дробей найти секретный ключ d и разложение модуля 93767386321457 (экспонента - 2091619) на множители. В ответе укажите секретный ключ.
Зашифровать открытый текст "СПИРТ_В_МЕДИЦИНСКИХ_ЦЕЛЯХ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 23514. Величины сдвигов:
позиций в алфавите. Порядок столбцов 23514. Величины сдвигов:  ,
, 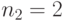 ,
,  ,
, 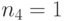 ,
, 
Два пользователя используют общий модуль N = 3127, но разные взаимно простые экспоненты 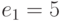 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 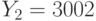 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверьте подлинность ЭЦП (11, 12) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПЛУТОН.
Зашифруйте открытый текст АБЕРРАЦИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(56, 419), значения случайных чисел для букв открытого текста k: 16, 2, 17, 19, 8, 4, 3, 2, 8, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Расшифровать текст 3-24.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100000110010011010000011.
, построить контрольную сумму для сообщения 1100000110010011010000011.
Шифротекст СЗАУПРТИС_РЕД_УБАЗАР_ОТИК получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-1.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число. (Примечание: знак _ обозначает пробел между словами.)
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Вычислить динамическое расстояние порядка (2,2) блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью  бит
бит
Провести первый раунд зашифрования открытого текста E26A 945F BE59 B5CC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 87046121832829 (экспонента - 2342047) на множители. В ответе укажите секретный ключ.
Три пользователя имеют модули 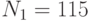 ,
, 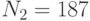 ,
, 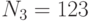 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 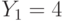 ,
, 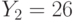 ,
,  . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Шифртекст (901439779, 10110110111111110111) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101839, q=98867. Найти открытый текст и введите его заглавными буквами.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6686. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 53, значения цифровой подписи: r = 22; s = 30. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7135. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 50; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (5, 2) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Три пользователя имеют модули 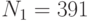 ,
,  ,
, 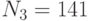 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 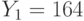 ,
, 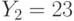 ,
,  . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Расшифровать фразу _ТОЬВО_ВМЫОПРГИИСУ_ПЛЙ_ОП, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Вычислить динамическое расстояние порядка (2,2) блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью  бит
бит
Даны значения модуля шифрования N = 3901 и открытого ключа e = 343. Используя метод факторизации Ферма, найти значение закрытого ключа.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101000011100000001111.
, построить контрольную сумму для сообщения 1110101000011100000001111.
Дан шифртекст 10, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 4-12.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Расшифровать сообщение 5-3.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-20.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Зашифровать открытый текст "МАТЕМАТИКА_ГИМНАСТИКА_УМА". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 35214. Величины сдвигов:
позиций в алфавите. Порядок столбцов 35214. Величины сдвигов: 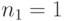 ,
, 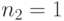 ,
,  ,
,  ,
, 
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст СИНТЕЗ.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Три пользователя имеют модули  ,
, 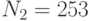 ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 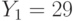 ,
, 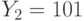 ,
, 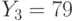 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Сообщение 1097 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {4,6,11,23,45,92,186}, m=369 и n=31. В ответе укажите исходное сообщение.
Шифртекст (8446011652, 10111001000000000000) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101603, q=99871. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (726, 608)}; {(188, 93), (395, 337)}; |
| {(440, 539), (163, 513)}; {(188, 93), (269, 187)}; |
| {(725, 195), (177, 562)}; {(188, 93), (115, 509)}; |
| {(188, 93), (734, 170)}; {(745, 210), (110, 622)}; |
| {(179, 275), (576, 286)}; {(188, 93), (325, 297)} |
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Проверить действительность подписей (10, 153), (11, 133) для сообщения с известным значением хэш-свертки 141 и открытым ключом проверки (35,374). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3521. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 28, значения цифровой подписи: r = 18; s = 31. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Применением цепных дробей найти секретный ключ d и разложение модуля 42982346145803 (экспонента - 4777621) на множители. В ответе укажите секретный ключ.
Провести первый раунд зашифрования открытого текста 991C 9E65 9A45 BD8C шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Сообщение 516 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,3,7,13,27,55,109}, m=218 и n=131. В ответе укажите исходное сообщение.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101111101111101101100100.
, построить контрольную сумму для сообщения 1101111101111101101100100.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111011100110110000001001.
, построить контрольную сумму для сообщения 1111011100110110000001001.
Шифротекст ЭЕМЕФРДЫ_ИЗГРУАЖНЫ_ЕВОЗУ_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-21.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Зашифровать открытый текст "НЕ_ВКЛЮЧАТЬ_РАБОТАЮТ_ЛЮДИ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 41325. Величины сдвигов:
позиций в алфавите. Порядок столбцов 41325. Величины сдвигов:  ,
, 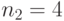 ,
,  ,
, 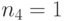 ,
, 
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=47, x=16.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ОВАЛ
или КРУГ
- устойчивее к действию этой программы?
Применением цепных дробей найти секретный ключ d и разложение модуля 85609460573249 (экспонента - 2448539) на множители. В ответе укажите секретный ключ.
Расшифровать текст 3-19.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Дано: модуль шифрования N = 3953, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2402 на открытом ключе (N, e) по алгоритму RSA.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙМЕР.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=43, x=12.
Чей компьютер он взломает быстрее?
Провести первый раунд зашифрования открытого текста FAAA A9D9 D006 8DC3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 3474 на открытом ключе (N, e) по алгоритму RSA.
Применением цепных дробей найти секретный ключ d и разложение модуля 55925060669503 (экспонента - 4156793) на множители. В ответе укажите секретный ключ.
Дан шифртекст 117, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=1 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Три пользователя имеют модули 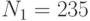 ,
, 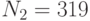 ,
, 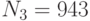 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 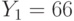 ,
, 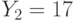 ,
, 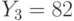 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Проверить действительность подписей (166, 213), (3, 188) для сообщения с известным значением хэш-свертки 45 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать текст 3-2.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-21.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЛОГИКА.
Вычислить динамическое расстояние порядка (2,2) блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью  бит
бит
Даны значения модуля шифрования N = 3569 и открытого ключа e = 1013. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 62781628076903 (экспонента - 3804071) на множители. В ответе укажите секретный ключ.
Зашифруйте открытый текст НЕЭТИЧНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 14, 18, 11, 11, 6, 6, 17, 2, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (416, 696). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (10, 163), (31, 79) для сообщения с известным значением хэш-свертки 214 и открытым ключом проверки (73,63). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверьте подлинность ЭЦП (3, 2) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (562, 89). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Зашифровать открытый текст "ВЫСОКИЙ_УРОВЕНЬ_ОПАСНОСТИ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 53421. Величины сдвигов:
позиций в алфавите. Порядок столбцов 53421. Величины сдвигов: 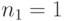 ,
, 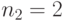 ,
,  ,
,  ,
, 
Расшифровать фразу _ЕТИЕИ_ЛО_АКАЗЖС_.ЩТЛУТС_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-10.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Зашифровать открытый текст "КОНВЕРТ_С_КЛЮЧОМ_В_ЯЧЕЙКЕ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 24315. Величины сдвигов:
позиций в алфавите. Порядок столбцов 24315. Величины сдвигов:  ,
, 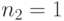 ,
,  ,
,  ,
, 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Два пользователя используют общий модуль N = 2701, но разные взаимно простые экспоненты 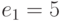 и
и 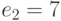 . Пользователи получили шифртексты
. Пользователи получили шифртексты 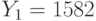 и
и 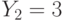 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Сообщение 505 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,3,5,13,23,49,99}, m=195 и n=127. В ответе укажите исходное сообщение.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101100000111111010001011.
, построить контрольную сумму для сообщения 1101100000111111010001011.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=22 и k=25 системы цифровой подписи и подписываемый текст РОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Расшифровать фразу _ПАЕНЕ_ВИ_ЯНЕРЖЕ_ИСТИОКНЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 64.
Сообщение 945 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,4,7,14,29,57,116}, m=233 и n=64. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ПРОЛЕЖЕНЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 9, 5, 17, 2, 2, 2, 3, 17, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить действительность подписей (35, 236), (57, 230) для сообщения с известным значением хэш-свертки 10 и открытым ключом проверки (177,531). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ПИЛЮЛЯ
или БОЛЮСЫ
- устойчивее к действию этой программы?
Дано: модуль шифрования N = 2257, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 539 на открытом ключе (N, e) по алгоритму RSA.
Расшифровать сообщение 5-13.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Зашифровать открытый текст "ВВЕДЁН_КОММЕНДАНТСКИЙ_ЧАС". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 43152. Величины сдвигов:
позиций в алфавите. Порядок столбцов 43152. Величины сдвигов: 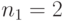 ,
, 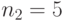 ,
,  ,
,  ,
, 
Расшифровать текст 3-25.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Зашифровать открытый текст "НЕ_ПОДСКОЛЬЗНИТЕСЬ_ПОМЫТО". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 31524. Величины сдвигов:
позиций в алфавите. Порядок столбцов 31524. Величины сдвигов:  ,
, 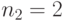 ,
,  ,
,  ,
, 
Вычислить динамическое расстояние порядка (2,2) блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста E37F C8BC F84A DFA3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 66.
Дан шифртекст 117, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Три пользователя имеют модули 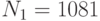 ,
,  ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 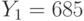 ,
, 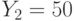 ,
, 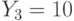 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Шифртекст (1439738115, 11000111110111010001) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100847, q=96331. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (651, 191)}; {(188, 93), (177, 562)}; |
| {(286, 136), (603, 562)}; {(440, 539), (588, 707)}; |
| {(72, 254), (269, 187)}; {(56, 419), (49, 568)}; |
| {(16, 416), (426, 662)}; {(425, 663), (557, 28)}; |
| {(188, 93), (149, 97)}; {(179, 275), (711, 341)} |
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 3, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙФУН.
Даны значения модуля шифрования N = 143 и открытого ключа e = 37. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 100.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ПЛАЦЕБО
или СПАСИБО
- устойчивее к действию этой программы?
Шифротекст ПООВРД_ЕРИБНАКЕ__ЕДВТА_ДС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Зашифровать открытый текст "КУРЕНИЕ_ВЛЕЧЕТ_РАК_ЛЕГКИХ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 42135. Величины сдвигов:
позиций в алфавите. Порядок столбцов 42135. Величины сдвигов: 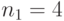 ,
, 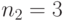 ,
,  ,
, 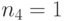 ,
, 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=37 и k=25 системы цифровой подписи и подписываемый текст ВВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ПЛИТА
или ПЛАТО
- устойчивее к действию этой программы?
Зашифровать открытый текст "ВЫСОКОКЛАССНЫЙ_КРИПТОГРАФ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 34125. Величины сдвигов:
позиций в алфавите. Порядок столбцов 34125. Величины сдвигов: 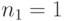 ,
, 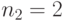 ,
,  ,
,  ,
, 
Расшифровать сообщение на английском языке 6-9.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-12.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - ШУБА
или СНЕГ
- устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Два пользователя используют общий модуль N = 3713, но разные взаимно простые экспоненты 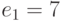 и
и 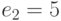 . Пользователи получили шифртексты
. Пользователи получили шифртексты 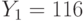 и
и  , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Шифртекст (3441665394, 10010010000100110110) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92051, q=94651. Найти открытый текст и введите его заглавными буквами.
Даны значения модуля шифрования N = 667 и открытого ключа e = 575. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 593.
Зашифруйте открытый текст РЕГРЕССОР с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425, 663), значения случайных чисел для букв открытого текста k: 6, 12, 16, 4, 9, 4, 19, 9, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (329, 304)}; {(440, 539), (59, 386)}; |
| {(618, 206), (543, 357)}; {(188, 93), (520, 749)}; |
| {(489, 468), (585, 211)}; {(179, 275), (707, 556)}; |
| {(596, 433), (419, 38)}; {(377, 456), (643, 94)}; |
| {(188, 93), (385, 749)}; {(725, 195), (150, 355)}; |
| {(725, 195), (197, 606)} |
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111110111100101001010100.
, построить контрольную сумму для сообщения 1111110111100101001010100.
Расшифровать фразу О_ДАВВРСТЕТСИМЯ_ВУ_Х_РПАК, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-9.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.Даны значения модуля шифрования N = 2911 и открытого ключа e = 359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=7 и k=23 системы цифровой подписи и подписываемый текст ТОР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Три пользователя имеют модули 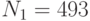 ,
, 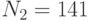 ,
, 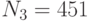 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов  ,
, 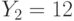 ,
, 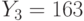 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - СТАТУС
или ЗОЛОТО
- устойчивее к действию этой программы?
Зашифровать открытый текст "МОЙТЕ_РУКИ_ДО_ЕДЫ_И_ПОСЛЕ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 43125. Величины сдвигов:
позиций в алфавите. Порядок столбцов 43125. Величины сдвигов: 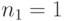 ,
, 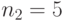 ,
,  ,
,  ,
, 
Дано: модуль шифрования N = 1961, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1382 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=48 и k=23 системы цифровой подписи и подписываемый текст РЫБА. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) - в скобках и без пробелов.
Расшифровать текст 3-11.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите четвертое слово заглавными буквами.
Дано: модуль шифрования N = 8051, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 6206 на открытом ключе (N, e) по алгоритму RSA.
Зашифруйте открытый текст ЛАТЫШСКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179,275), значения случайных чисел для букв открытого текста k: 15, 17, 12, 2, 2, 4, 8, 6, 17, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверьте подлинность ЭЦП (5, 5) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Расшифровать текст 3-6.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Провести первый раунд зашифрования открытого текста B89F F9A1 C5A5 8C39 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 48992988576733 (экспонента - 4545733) на множители. В ответе укажите секретный ключ.
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,3,5,10,21,42,88}, m=171 и n=23. В ответе укажите исходное сообщение.
Проверить действительность подписей (166, 186), (104, 103) для сообщения с известным значением хэш-свертки 115 и открытым ключом проверки (126,463). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,4,7,15,28,57,114}, m=227 и n=51. В ответе укажите исходное сообщение.
Даны значения модуля шифрования N = 2701 и открытого ключа e = 1507. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 52, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 249 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,2,7,11,23,47,92}, m=185 и n=29. В ответе укажите исходное сообщение.
Сообщение 390 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {3,4,9,17,34,69,137}, m=277 и n=99. В ответе укажите исходное сообщение.
Применением цепных дробей найти секретный ключ d и разложение модуля 64806601923671 (экспонента - 3676721) на множители. В ответе укажите секретный ключ.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (538, 325)}; {(725, 195), (176, 413)}; |
| {(425, 663), (689, 670)}; {(346, 242), (652, 315)}; |
| {(283, 493), (463, 736)}; {(16, 416), (744, 133)}; |
| {(179, 275), (542, 351)}; {(56, 419), (298, 225)}; |
| {(286, 136), (719, 538)}; {(568, 355), (319, 518)}; |
| {(16, 416), (704, 46)} |
Расшифровать сообщение 4-15.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-6.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - МАКАКИ
или ЖИРАФЫ
- устойчивее к действию этой программы?
Даны значения модуля шифрования N = 3397 и открытого ключа e = 2477. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 34542035262313 (экспонента - 4727621) на множители. В ответе укажите секретный ключ.
Два пользователя используют общий модуль N = 7081, но разные взаимно простые экспоненты 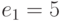 и
и 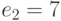 . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 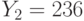 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Шифртекст (432159239, 01101010010011011001) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93503, q=97007. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст НОВЕНЬКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425,663), значения случайных чисел для букв открытого текста k: 19, 12, 13, 2, 12, 14, 19, 18, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (279, 398)}; {(568, 355), (295, 219)}; |
| {(16, 416), (724, 229)}; {(346, 242), (730, 240)}; |
| {(72, 254), (334, 226)}; {(188, 93), (310, 169)}; |
| {(72, 254), (36, 664)}; {(179, 275), (481, 369)}; |
| {(188, 93), (236, 39)}; {(377, 456), (438, 711)}; |
| {(377, 456), (307, 58)} |
Дан шифртекст 90, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 5-1.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Два пользователя используют общий модуль N = 4183, но разные взаимно простые экспоненты 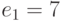 и
и 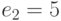 . Пользователи получили шифртексты
. Пользователи получили шифртексты 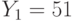 и
и  , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Провести первый раунд зашифрования открытого текста 97A0 9BD3 DF10 C86A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 50824793010569 (экспонента - 4440901) на множители. В ответе укажите секретный ключ.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (675, 505)}; {(72, 254), (611, 579)}; |
| {(72, 254), (727, 686)}; {(489, 468), (39, 171)}; |
| {(72, 254), (531, 354)}; {(568, 355), (36, 87)}; |
| {(188, 93), (588, 44)}; {(618, 206), (70, 195)}; |
| {(568, 355), (267, 81)}; {(56, 419), (525, 674)} |
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль - трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=23, x=14.
Чей компьютер он взломает быстрее?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1010001111010000011110000.
, построить контрольную сумму для сообщения 1010001111010000011110000.
Расшифровать сообщение на английском языке 6-3.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.Сообщение 537 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {2,3,7,15,29,57,115}, m=230 и n=43. В ответе укажите исходное сообщение.
Три пользователя имеют модули 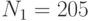 ,
, 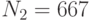 ,
, 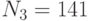 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 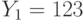 ,
,  ,
, 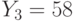 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Вычислить динамическое расстояние порядка (2,2) блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью  бит
бит
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А - 0, Б -1, ..., Я - 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a - число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей - РАБОТА
или ОТПУСК
- устойчивее к действию этой программы?
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7707. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 11; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать фразу МДЕ_Ж__ВТАЕТВТОНЧЕИЕН_ДЯЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗДЕЛ.
Расшифровать сообщение 4-2.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110000001000000101010101.
, построить контрольную сумму для сообщения 1110000001000000101010101.
Расшифровать текст 3-12.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью  бит
бит
Даны значения модуля шифрования N = 391 и открытого ключа e = 47. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 262.
Применением цепных дробей найти секретный ключ d и разложение модуля 99595193774911 (экспонента - 1908299) на множители. В ответе укажите секретный ключ.
Три пользователя имеют модули 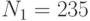 ,
, 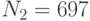 ,
, 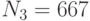 . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов 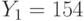 ,
, 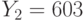 ,
, 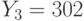 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Дан шифртекст 49, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 5-19.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Зашифровать открытый текст "ВНИМАТЕЛЬНЕЙ_НА_ПОВОРОТАХ". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 32451. Величины сдвигов:
позиций в алфавите. Порядок столбцов 32451. Величины сдвигов: 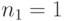 ,
, 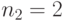 ,
,  ,
,  ,
, 
Вычислить динамическое расстояние порядка (2,2) блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью  бит
бит
Дано: модуль шифрования N = 3071, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1058 на открытом ключе (N, e) по алгоритму RSA.
Два пользователя используют общий модуль N = 3431, но разные взаимно простые экспоненты 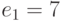 и
и 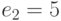 . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и 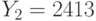 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111000110001000100101001.
, построить контрольную сумму для сообщения 1111000110001000100101001.
Провести первый раунд зашифрования открытого текста FE2D FEEA B158 BE38 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 124.
Даны значения модуля шифрования N = 4717 и открытого ключа e = 523. Используя метод факторизации Ферма, найти значение закрытого ключа.
Два пользователя используют общий модуль N = 3649, но разные взаимно простые экспоненты 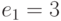 и
и 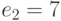 . Пользователи получили шифртексты
. Пользователи получили шифртексты 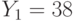 и
и 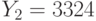 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Дан шифртекст 84, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Зашифруйте открытый текст РЕПАРАЦИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(435, 663), значения случайных чисел для букв открытого текста k: 12, 11, 18, 7, 16, 18, 17, 2, 3, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Сообщение 792 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,7,9,19,37,75,152}, m=307 и n=63. В ответе укажите исходное сообщение.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЭЛЛИПС.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|
Даны значения модуля шифрования N = 319 и открытого ключа e = 51. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 209.
Зашифруйте открытый текст НИЩЕНСКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 2, 2, 7, 11, 19, 4, 2, 15, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Три пользователя имеют модули 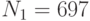 ,
, 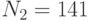 ,
,  . Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов
. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение, дошедшее до них в виде шифртекстов  ,
, 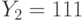 ,
, 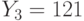 . Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
. Найти исходный текст, пользуясь атакой на основе китайской теоремы об остатках.
Провести первый раунд зашифрования открытого текста CF85 F7CE F928 C262 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью  бит
бит
Зашифровать открытый текст "УЧЕНИЕ_СВЕТ_НЕУЧЕНИЕ_ТЬМА". Сохраняя пробелы между словами, записать его в таблицу  . Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква
. Начало в первой строке, текст записывается слева направо, переходя с каждой строки на следующую, после чего нужно переставить столбцы в соответствии с ключом. Затем к каждому столбцу применить простую замену: каждая буква  -го столбца циклически сдвигается справо на
-го столбца циклически сдвигается справо на  позиций в алфавите. Порядок столбцов 32154. Величины сдвигов:
позиций в алфавите. Порядок столбцов 32154. Величины сдвигов: 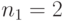 ,
, 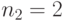 ,
,  ,
,  ,
, 
Зашифруйте открытый текст ЗВЕЗДОЧКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 11, 17, 10, 10, 5, 2, 10, 19, 4, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (295, 219)}; {(618, 206), (646, 706)}; |
| {(440, 539), (573, 583)}; {(16, 416), (694, 581)}; |
| {(179, 275), (585, 540)}; {(377, 456), (701, 570)}; |
| {(618, 206), (67, 667)}; {(286, 136), (36, 664)}; |
| {(72, 254), (727, 65)}; {(568, 355), (438, 40)} |
Провести первый раунд зашифрования открытого текста D14E C9C9 F441 8039 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Расшифровать фразу МИКСО_ВЫ_ЕУБ_АДПЛДЕУОНСНИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Два пользователя используют общий модуль N = 1927, но разные взаимно простые экспоненты 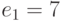 и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты 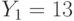 и
и 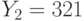 , которые были получены в результате зашифрования на экспонентах
, которые были получены в результате зашифрования на экспонентах  и
и  соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
соотетственно одного и того же сообщения. Найти исходное сообщение методом бесключевого чтения.
Сообщение 429 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {1,4,6,14,27,55,109}, m=217 и n=73. В ответе укажите исходное сообщение.
Расшифровать сообщение на английском языке 6-16.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Шифротекст КУАМКЛТУОЯ_ЖРЕУРЗ_РАЖНЯ_Е получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Дан шифртекст 107, а также значения модуля шифрования N = 209 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Зашифруйте открытый текст ЛАТЕНТНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 9, 10, 13, 2, 2, 12, 12, 5, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить динамическое расстояние порядка (2,2) блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью  бит
бит
Сообщение 492 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {3,4,8,17,33,67,138}, m=271 и n=65. В ответе укажите исходное сообщение.
Расшифровать текст 3-10.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс "Classic", специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Шифртекст (6737479610, 00010100110100110110) получен из слова в алфавите {А, Б, ..., Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93763, q=90011. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (268, 597)}; {(725, 195), (310, 582)}; |
| {(618, 206), (59, 365)}; {(440, 539), (371, 14)}; |
| {(188, 93), (348, 27)}; {(72, 254), (434, 136)}; |
| {(16, 416), (623, 166)}; {(188, 93), (235, 19)}; |
| {(440, 539), (660, 275)}; {(188, 93), (434, 615)}; |
| {(725, 195), (73, 679)}; {(188, 93), (642, 53)} |
Расшифровать сообщение 5-11.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.Расшифровать сообщение на английском языке 6-5.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Вычислить динамическое расстояние порядка (2,2) блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью  бит
бит
Дано: модуль шифрования N = 4307, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 983 на открытом ключе (N, e) по алгоритму RSA.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование:  , где
, где  - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
- числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 332) =675119(mod 332)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.
Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы  . Триграмме ТЛЛ соответствует вектор
. Триграмме ТЛЛ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> УДЬ, триграмме РЙЁ соответствует вектор
-> УДЬ, триграмме РЙЁ соответствует вектор  , результат зашифрования:
, результат зашифрования:  -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
-> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.
Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст АНАЛИЗ.
Сообщение 402 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа - {6,7,14,29,57,114,229}, m=457 и n=150. В ответе укажите исходное сообщение.
Расшифровать сообщение на английском языке 6-19.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) - в сокбках и без пробелов.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (128, 672)}; {(489, 468), (282, 341)}; |
| {(489, 468), (45, 720)}; {(72, 254), (227, 299)}; |
| {(188, 93), (251, 506)}; {(72, 254), (319, 518)}; |
| {(745, 210), (129, 659)}; {(286, 136), (515, 684)}; |
| {(568, 355), (395, 414)} |
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
| K: |
|

 над полем
над полем 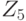 .
. над полем
над полем 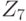 .
. -алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.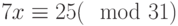 с помощью цепных дробей.
с помощью цепных дробей. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.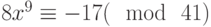 с помощью индексов.
с помощью индексов. на 45.
на 45.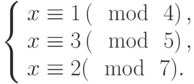
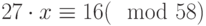 .
.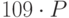 .
.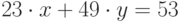 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)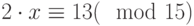 .
.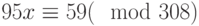 с помощью цепных дробей.
с помощью цепных дробей.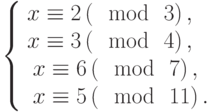
 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) на 13.
на 13. при a = 5124; b = 129; c = 59466.
при a = 5124; b = 129; c = 59466. .
.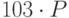 .
.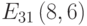 порядка 25.
порядка 25.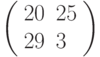 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.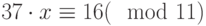 .
.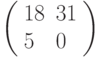 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.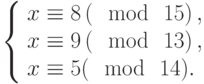
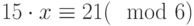 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) порядка 38.
порядка 38.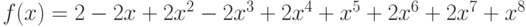 над полем
над полем 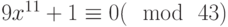 с помощью индексов.
с помощью индексов.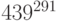 на 60.
на 60. . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)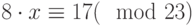 .
.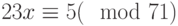 с помощью цепных дробей.
с помощью цепных дробей.
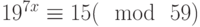 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) на 100.
на 100. над полем
над полем 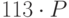 .
.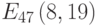 порядка 55.
порядка 55. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.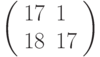 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.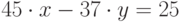 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)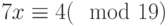 с помощью цепных дробей.
с помощью цепных дробей.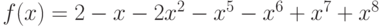 над полем
над полем 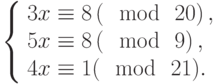
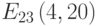 порядка 28.
порядка 28. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.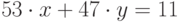 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 35.
на 35.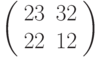 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.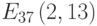 порядка 44.
порядка 44.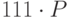 .
.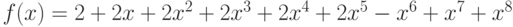 над полем
над полем 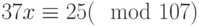 с помощью цепных дробей.
с помощью цепных дробей.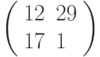 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.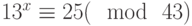 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) порядка 28.
порядка 28. .
.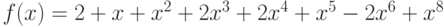 над полем
над полем  на 7.
на 7.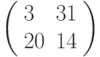 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.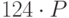 .
.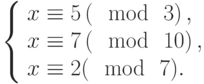
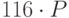 .
.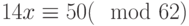 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)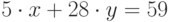 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) .
.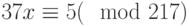 с помощью цепных дробей.
с помощью цепных дробей.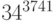 на 2.
на 2. порядка 38.
порядка 38.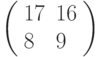 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.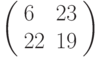 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.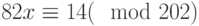 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.) с помощью индексов.
с помощью индексов.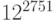 на 5.
на 5.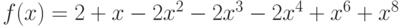 над полем
над полем  .
.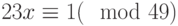 с помощью цепных дробей.
с помощью цепных дробей.
 на 100.
на 100.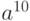 и
и 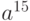 .
.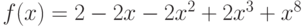 над полем
над полем 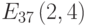 порядка 42.
порядка 42.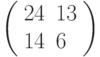 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.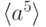 ?
?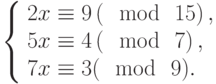
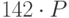 .
.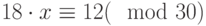 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)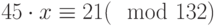 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)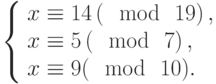
 на 14.
на 14.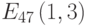 порядка 54.
порядка 54.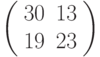 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.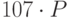 .
.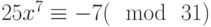 с помощью индексов.
с помощью индексов.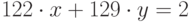 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)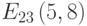 порядка 32.
порядка 32. . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)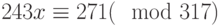 с помощью цепных дробей.
с помощью цепных дробей.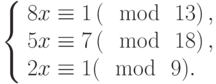
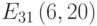 порядка 32.
порядка 32.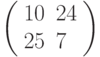 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.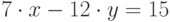 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) над полем
над полем 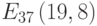 порядка 36.
порядка 36.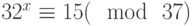 с помощью индексов.
с помощью индексов.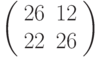 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)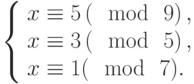
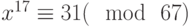 с помощью индексов.
с помощью индексов.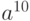 и
и 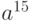 .
.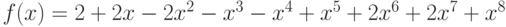 над полем
над полем  порядка 40.
порядка 40.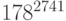 на 22.
на 22.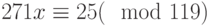 с помощью цепных дробей.
с помощью цепных дробей.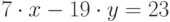 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)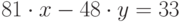 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)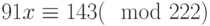 с помощью цепных дробей.
с помощью цепных дробей.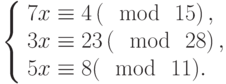
 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)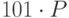 .
.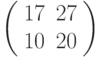 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.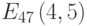 порядка 48.
порядка 48.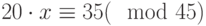 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)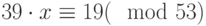 .
.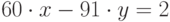 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)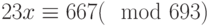 с помощью цепных дробей.
с помощью цепных дробей.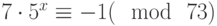 с помощью индексов.
с помощью индексов. на 11.
на 11.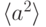 ?
?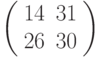 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. с помощью индексов.
с помощью индексов.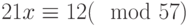 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)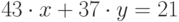 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 11.
на 11.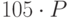 .
.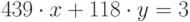 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)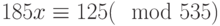 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)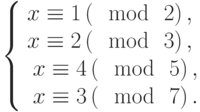
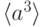 ?
?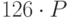 .
.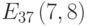 порядка 40.
порядка 40.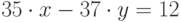 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)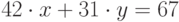 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)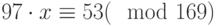 .
.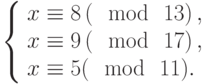
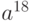 и
и 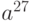 .
.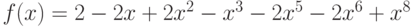 над полем
над полем 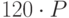 .
. на 12.
на 12.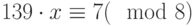 .
.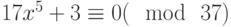 с помощью индексов.
с помощью индексов.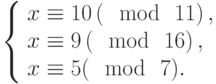
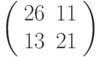 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.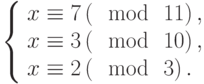
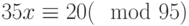 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)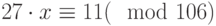 .
.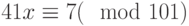 с помощью цепных дробей.
с помощью цепных дробей. на 1000.
на 1000.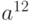 и
и 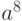 .
. порядка 33.
порядка 33.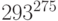 на 48.
на 48. . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)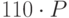 .
.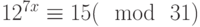 с помощью индексов.
с помощью индексов. на 13.
на 13.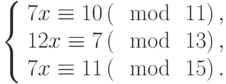
 на 11.
на 11.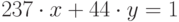 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)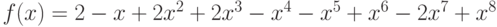 над полем
над полем  .
.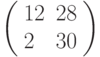 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.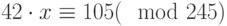 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)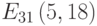 порядка 30.
порядка 30.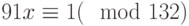 с помощью цепных дробей.
с помощью цепных дробей.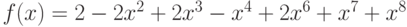 над полем
над полем 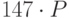 .
.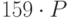 .
.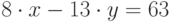 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)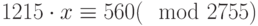 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) на 5.
на 5.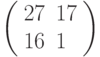 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.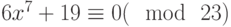 с помощью индексов.
с помощью индексов. .
.
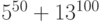 на 18.
на 18.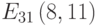 порядка 36.
порядка 36.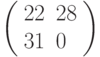 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.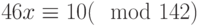 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)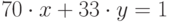 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) с помощью цепных дробей.
с помощью цепных дробей. с помощью индексов.
с помощью индексов.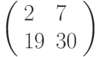 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.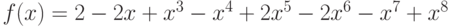 над полем
над полем  с помощью индексов.
с помощью индексов.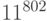 на 1000.
на 1000.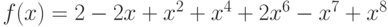 над полем
над полем 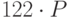 .
.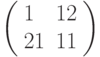 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.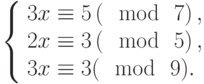
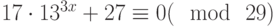 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)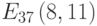 порядка 32.
порядка 32.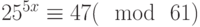 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)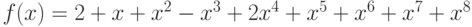 над полем
над полем  с помощью индексов.
с помощью индексов.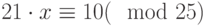 .
.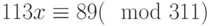 с помощью цепных дробей.
с помощью цепных дробей.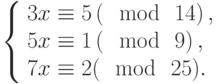
 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)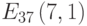 порядка 44.
порядка 44. на 7.
на 7.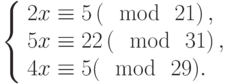
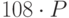 .
.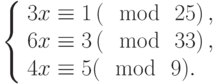
 над полем
над полем 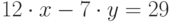 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 7.
на 7.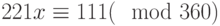 с помощью цепных дробей.
с помощью цепных дробей.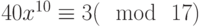 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)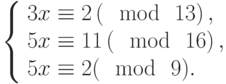
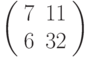 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.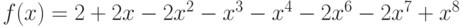 над полем
над полем  на 14.
на 14.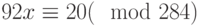 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)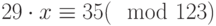 .
.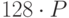 .
.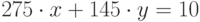 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)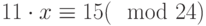 .
.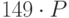 .
.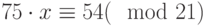 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) .
.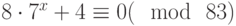 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) .
.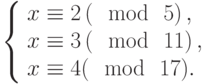
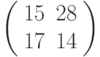 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.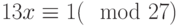 с помощью цепных дробей.
с помощью цепных дробей.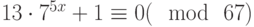 с помощью индексов.
с помощью индексов.