Жидкость заполняет двугранный угол, образованный взаимно перпендикулярными плоскими стенками. Найти составляющую поля скорости  изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
(Отметьте один правильный вариант ответа.)
Варианты ответа
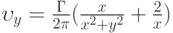
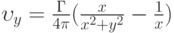 (Верный ответ)
(Верный ответ)
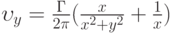

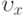 изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона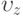 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 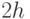 . Решение искать в виде
. Решение искать в виде 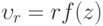 ,
, 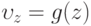 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей)
- уравнения плоскостей)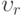 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости  и давление вдоль пластин постоянно
и давление вдоль пластин постоянно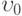 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 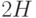 . Коэффициент вязкости:
. Коэффициент вязкости: 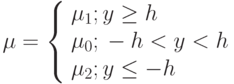 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
, 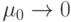 )
) (
( (
(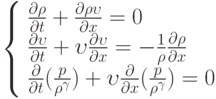 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 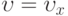 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 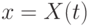 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров 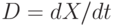 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения