Пусть 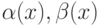 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
(Отметьте один правильный вариант ответа.)
Варианты ответа
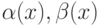 одного порядка
одного порядка
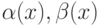 эквивалентны
эквивалентны
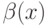 более высокого порядка, чем
более высокого порядка, чем 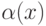 (Верный ответ)
(Верный ответ)
не сравнимы
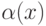 более высокого порядка, чем
более высокого порядка, чем 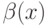

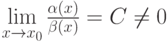 . Тогда
. Тогда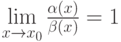 . Тогда
. Тогда и
и 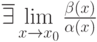 .Тогда
.Тогда 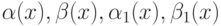 - бесконечно малые при
- бесконечно малые при 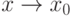 функции, причём
функции, причём 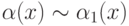 и
и 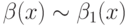 . Если
. Если 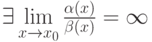 , то
, то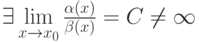 , то
, то и
и 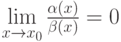 . Тогда
. Тогда так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при 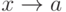 .
. 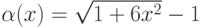 ,
, 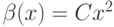 ,
, 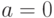
![\alpha(x)=\sqrt[3]{1+3x^3}-1](https://intuit.ru//sites/default/files/tex_cache/9e8eb11009ce192ae4b88e61006b0401.png) ,
, 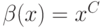 ,
, 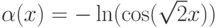 ,
, 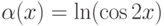 ,
, 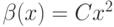 ,
,