Математический анализ - 1

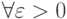Пусть число - предел последовательности $\{a_n\}$ . Тогда $\forall \varepsilon > 0$ вне окрестности 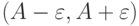$(A - \varepsilon, A + \varepsilon)$ лежит

(Отметьте один правильный вариант ответа.)

Варианты ответа

конечное число элементов $\{a_n\}$ (Верный ответ)

бесконечное число элементов $\{a_n\}$

Похожие вопросы

Если последовательность $\{a_n\}$ такова, что $\forall \varepsilon > 0$ неравенство $|a_n| > \varepsilon$ выполняется лишь для конечного числа членов последовательности, то её предел $\lim\limits_{n \to \infty} {a_n}$ равен

По определению, число

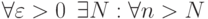называется пределом последовательности $\{a_n\}$ , если $\forall \varepsilon > 0 \enskip \exists N : \forall n > N$ справедливо неравенство

Пусть для функции f(x)

выполнено условие $\forall \varepsilon > 0 \enskip \exists \delta (\varepsilon): \forall x',x'' \in (a,b) \enskip |x' - x''| < \delta \Rightarrow |f(x') - f(x'')| < \varepsilon$ . Это означает, что функция f(x)

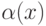Функция $\alpha (x)$ называется бесконечно малой функцией при

, стремящемся к

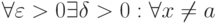
, если $\forall \varepsilon > 0 \exists \delta > 0 : \forall x \neq a$

Если последовательность $\{a_n\}$ такова, что интервал (-M, M)

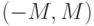при любом

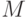содержит только конечное число членов последовательности, то ее предел $\lim\limits_{n \to \infty} {a_n}$ равен

Пусть

определена в некоторой окрестности точки

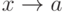и $\lim\limits_{x \to a} {f(x)} = A + \alpha (x)$ . Тогда ( $\alpha (x)$ - б.м.ф. при $x \to a$ ). Тогда предел функции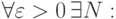 f(x)

Необходимое и достаточное условие сходимости последовательности $\{a_n\}$ (критерий Коши ) формулируется следующим образом: $\forall \varepsilon > 0 \, \exists N :$

Пусть для функции f(x)

в окрестности точки x_0

существует производная

-го порядка, непрерывная в x_0

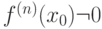и $f^{(n)}(x_0) \neg 0$ - первая отличная от нуля производная. Тогда x_0

- точка максимума f(x)

, если

Пусть для функции f(x)

в окрестности точки x_0

существует производная

-го порядка и $f^{(n)}(x_0) \neg 0$ - первая отличная от нуля производная. Тогда x_0

- не является точкой минимума и максимума f(x)

, если

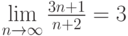Пусть $\lim\limits_{n \to \infty} {\frac {3n+1} {n+2}} = 3$ . Тогда, по определению предела, $\forall \varepsilon > 0 \enskip \exists N : \forall n > N$

Математический анализ - 1

Пусть число - предел последовательности . Тогда вне окрестности лежит

Пусть число - предел последовательности $\{a_n\}$ . Тогда $\forall \varepsilon > 0$ вне окрестности $(A - \varepsilon, A + \varepsilon)$ лежит