По определению, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если
(Отметьте один правильный вариант ответа.)
Варианты ответа
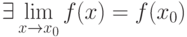 (Верный ответ)
(Верный ответ)
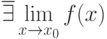
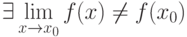

 называется непрерывной в точке
называется непрерывной в точке  , если
, если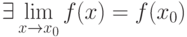 (Верный ответ)
(Верный ответ)
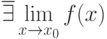
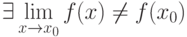
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет минимум, если её производная
имеет минимум, если её производная  при переходе через точку
при переходе через точку 
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет экстремум, если её производная
имеет экстремум, если её производная  при переходе через точку
при переходе через точку 
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет максимум, если её производная
имеет максимум, если её производная  при переходе через точку
при переходе через точку 
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка, непрерывная в
-го порядка, непрерывная в  и
и 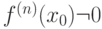 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка максимума
- точка максимума  , если
, если функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой максимума для
была точкой максимума для  :
: функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой минимума для
была точкой минимума для  :
: