Вычислить неорпеделенный интеграл методом замены переменной  и выбрать правильный вариант:
и выбрать правильный вариант:
(Отметьте один правильный вариант ответа.)
Варианты ответа
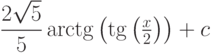
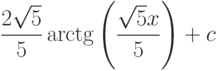
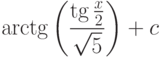
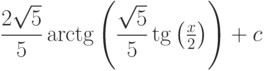 (Верный ответ)
(Верный ответ)

 и выбрать правильный вариант:
и выбрать правильный вариант: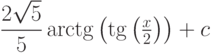
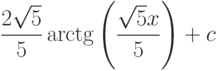
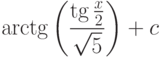
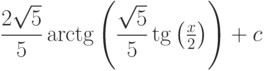 (Верный ответ)
(Верный ответ)