Выбрать наилучший вариант замены переменных на  и
и  при вычислении интеграла
при вычислении интеграла 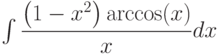 , используя метод интегрирования по частям
, используя метод интегрирования по частям
(Отметьте один правильный вариант ответа.)
Варианты ответа
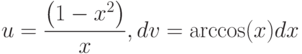
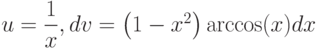

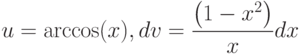 (Верный ответ)
(Верный ответ)

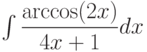 , используя метод интегрирования по частям
, используя метод интегрирования по частям , используя метод интегрирования по частям
, используя метод интегрирования по частям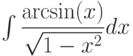 , используя метод интегрирования по частям
, используя метод интегрирования по частям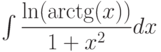 , используя метод интегрирования по частям
, используя метод интегрирования по частям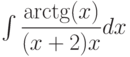 , используя метод интегрирования по частям
, используя метод интегрирования по частям , используя метод интегрирования по частям
, используя метод интегрирования по частям , используя метод интегрирования по частям
, используя метод интегрирования по частям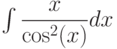 , используя метод интегрирования по частям
, используя метод интегрирования по частям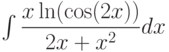 , используя метод интегрирования по частям
, используя метод интегрирования по частям , используя метод интегрирования по частям
, используя метод интегрирования по частям