Прикладная статистика

<<- Назад к вопросам

- случайная величина.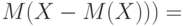

(Отметьте один правильный вариант ответа.)

Варианты ответа

0(Верный ответ)

Похожие вопросы

Если

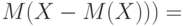
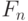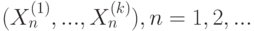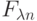обозначает совместную функцию распределения k-мерного случайного вектора $(X_n^{(1)},...,X_n^{(k)}), n=1,2,...$ и $F_{\lambda n}$ - функция распределения линейной комбинации 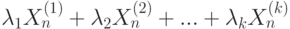$\lambda_1X_n^{(1)}+\lambda_2X_n^{(2)}+...+\lambda_k X_n^{(k)}$ , то необходимое и достаточное условие для сходимости F_n

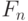к некоторой k-мерной функции распределения

состоит в том, что ...

- случайная величина. M(25X)=

Согласно центральной предельной теореме для одинаково распределенных слагаемых, если X_1,X_2,...,X_n

- независимые одинаково распределенные случайные величины с математическими ожиданиями M(X_i)=m

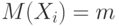и дисперсиями 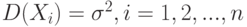$D(X_i)=\sigma^2, i=1,2,...,n$ , то для любого действительного числа

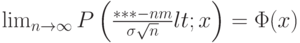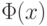существует предел $\lim_{n\rightarrow\infty}P\left(\frac{*** - nm}{\sigma\sqrt{n}} lt; x\right)=\Phi(x)$ где $\Phi(x)$ - функция стандартного нормального распределения. На месте *** должно быть

Согласно центральной предельной теореме для одинаково распределенных слагаемых, если X_1,X_2,...,X_n

- независимые одинаково распределенные случайные величины с математическими ожиданиями M(X_i)=m

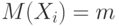и дисперсиями 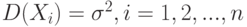$D(X_i)=\sigma^2, i=1,2,...,n$ , то для любого действительного числа

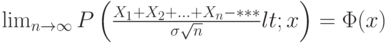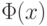существует предел $\lim_{n\rightarrow\infty}P\left(\frac{X_1+X_2+...+X_n - ***}{\sigma\sqrt{n}}lt; x\right)=\Phi(x)$ где $\Phi(x)$ - функция стандартного нормального распределения. На месте *** должно быть