Пусть 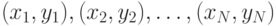 – обучающая выборка, причем
– обучающая выборка, причем  . Указать правильную формулировку задачи нахождения оптимальной разделяющей гиперплоскости (в случае линейно разделимых классов):
. Указать правильную формулировку задачи нахождения оптимальной разделяющей гиперплоскости (в случае линейно разделимых классов):
(Отметьте один правильный вариант ответа.)
Варианты ответа
 при ограничениях
при ограничениях  (Верный ответ)
(Верный ответ)
 при ограничениях
при ограничениях 

 Какое изображение получится в результате применения оператора Собеля с ядром
Какое изображение получится в результате применения оператора Собеля с ядром 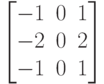 ? Граница дополняется посредством дублирования.
? Граница дополняется посредством дублирования. Какое изображение получится в результате применения оператора Собеля с ядром
Какое изображение получится в результате применения оператора Собеля с ядром  ? Граница дополняется посредством дублирования.
? Граница дополняется посредством дублирования.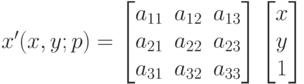 ?
?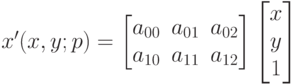 ?
?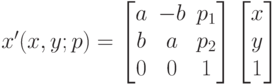 ?
?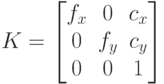 – матрица внутренних параметров камеры, R – матрица поворота объекта, T – вектор его параллельного переноса, то чему равна проекционная матрица P?
– матрица внутренних параметров камеры, R – матрица поворота объекта, T – вектор его параллельного переноса, то чему равна проекционная матрица P?