При каком значении а многочлен 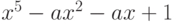 имеет -1 корнем не ниже второй кратности?
имеет -1 корнем не ниже второй кратности?
(Отметьте один правильный вариант ответа.)
Варианты ответа
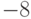
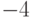

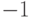
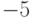 (Верный ответ)
(Верный ответ)
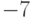
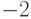
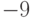
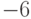

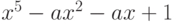 имеет -1 корнем не ниже второй кратности?
имеет -1 корнем не ниже второй кратности?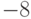
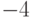

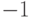
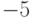 (Верный ответ)
(Верный ответ)
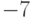
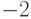
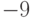
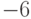
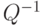 от ортонормированного базиса
от ортонормированного базиса 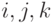 в пространстве
в пространстве 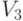 геометрических векторов к базису
геометрических векторов к базису 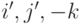 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?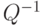 от ортонормированного базиса
от ортонормированного базиса 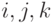 в пространстве
в пространстве 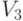 геометрических векторов к базису
геометрических векторов к базису 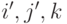 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов? в правом ортонормированном базисе
в правом ортонормированном базисе 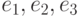 , если
, если 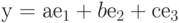 (а, b, с — заданные числа); у — фиксированный вектор линейного пространства
(а, b, с — заданные числа); у — фиксированный вектор линейного пространства 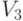 ,
,  — оператор, действие которого на любой вектор
— оператор, действие которого на любой вектор  из
из 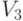 задается равенством
задается равенством ![\widehat А х = [х , у], где [х , у]](https://intuit.ru//sites/default/files/tex_cache/bb53811acdf9d1592baa14383e89273e.png) — векторное произведение вектора
— векторное произведение вектора  на вектор
на вектор  ?
?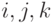 в пространстве
в пространстве 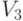 геометрических векторов к базису
геометрических векторов к базису 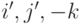 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?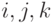 в пространстве
в пространстве 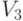 геометрических векторов к базису
геометрических векторов к базису 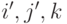 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?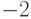 и
и 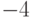 ?
?