Функция 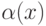 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 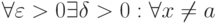
(Отметьте один правильный вариант ответа.)
Варианты ответа
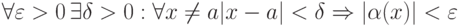 (Верный ответ)
(Верный ответ)

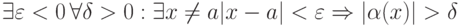


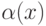 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 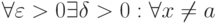
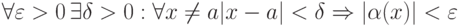 (Верный ответ)
(Верный ответ)

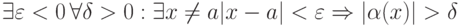

 такова, что
такова, что 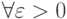 неравенство
неравенство  выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел  равен
равен