Пусть задача линейного программирования сформулирована следующим образом: максимизировать cTx при ограничениях Аx≤b; x≥0;. Данная форма записи является:
(Отметьте один правильный вариант ответа.)
Варианты ответа
канонической формой
матричной формой(Верный ответ)
общей формой

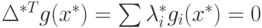 . Тогда вектор
. Тогда вектор