Для табличного симплекс – метода в качестве начального базиса выбран базис из свободных переменных, для которых ci = 0. Соответствующее значение целевой функции определяется соотношением a00 = Σcixi = 0, i є I. Тогда оценки для всех небазисных переменных равны:
(Отметьте один правильный вариант ответа.)
Варианты ответа
Δj=a0j=cj
Δj=a0j=-cj(Верный ответ)
Δj=-a0j=-cj

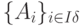 , которому соответствует псевдоплан
, которому соответствует псевдоплан