Введение в теорию графов

Какие дуги являются петлями в графе на рисунке?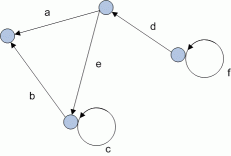

Выполнить операцию пересечения G₁ G₂ для графов, показанных на рисунке 1

Методом Мальгранжа разбить граф, представленный матрицей смежности, на максимальные сильно связные подграфы
X₁ X₂ X₃ X₄ X₅ X₆ X₇ X₈
X₁ 0 1 0 0 0 0 0 1
X₂ 1 0 1 0 1 0 0 0
X₃ 0 0 0 1 1 0 0 0
X₄ 0 0 0 0 0 1 0 0
X₅ 0 0 1 0 0 0 1 0
X₆ 0 0 0 1 0 0 0 0
X₇ 1 0 0 0 1 1 0 0
X₈ 0 0 0 0 0 0 1 0

Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы.

Какие из приведенных на рисунке графов являются полными?

Для графа, представленного на рисунке, данаматрица смежности. Верно ли представлен граф?
матрица смежности
X₁ X₂ X₃ X₄
X₁ 1 1 0 0
X₂ 0 0 1 1
X₃ 0 0 0 0
X₄ 1 1 1 0

Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного на рисунке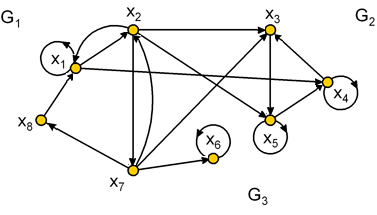

Найдите полустепени исхода и захода для вершины х₃ графа

Является ли граф на рисунке двудольным

Обновление пометок происходит по формуле:

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 3.

Для графа, приведенного на рисунке 1, найти матрицу контрдостижимости.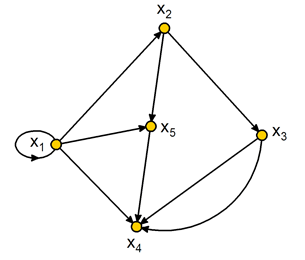
а
X₁ X₂ X₃ X₄ X₅
X₁ 1 0 0 0 0
Q= X₂ 1 1 0 0 0
X₃ 1 1 1 0 0
X₄ 1 0 1 1 1
X₅ 1 1 0 0 1
б
X₁ X₂ X₃ X₄ X₅
X₁ 1 0 0 0 0
Q= X₂ 1 1 0 0 0
X₃ 1 1 1 0 0
X₄ 1 1 1 1 1
X₅ 1 1 0 0 1
в
X₁ X₂ X₃ X₄ X₅
X₁ 1 0 0 0 0
Q= X₂ 1 1 0 0 0
X₃ 1 1 1 0 0
X₄ 1 1 1 1 0
X₅ 1 1 0 0 1

Найти максимальный сильно связанный подграф, включающий вершину C, для графа, матрица смежности которого представлена ниже
A B C D E F G K
A 1 1 0 0 1 0 0 0
B 0 0 1 0 1 1 0 0
C 0 0 1 0 1 0 0 0
D 0 0 0 0 0 0 0 1
E 0 0 0 0 0 1 0 0
F 1 0 0 0 0 0 1 0
G 0 0 0 0 0 0 0 1
K 0 0 0 1 0 0 0 0

Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его подграфами?

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х₅и х₆,

В графе G₆ , показанном на рис. 1 удалить вершину х₁. Результат представлен ниже в матричном виде
а
X₂ X₃
X₂ 0 1
X₃ 1 0
б
X₁ X₂
X₁ 0 1
X₂ 1 0
в
X₁ X₃
X₁ 0 1
X₃ 1 0

Какие из приведенных на рисунке графов являются слабо связными?

Методом Мальгранжа разбить граф, представленный ниже матрицей смежности, на подграфы
X₁ X₂ X₃ X₄ X₅ X₆ X₇
X₁ 1 1 0 1 0 0 0
X₂ 1 0 1 0 0 1 0
X₃ 0 0 0 0 1 0 0
X₄ 0 0 1 0 0 0 0
X₅ 0 0 0 1 0 0 0
X₆ 0 1 0 0 0 0 1
X₇ 1 0 0 0 0 0 0

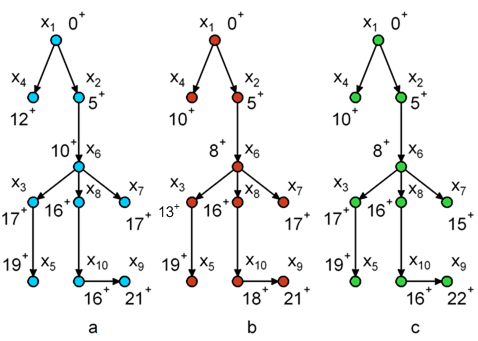
Найти кратчайший путь от вершины x₁ к вершине x₁₀ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б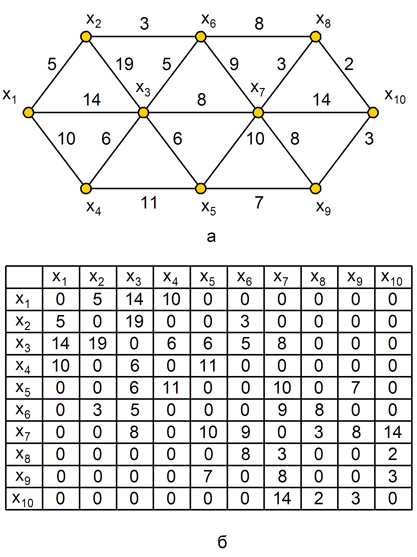

Построить орцепи максимальной длины из вершин A и B графа, изображенного на рисунке

Построить простые орцепи максимальной длины из вершин A и B графа, изображенного на рисунке

По матрице инциденций найти полустепени захода для Х₂
a₁ a₂ a₃ a₄ a₅ a₆ a₇ a₈ a₉ a₁₀
X₁ 2 -1 1 0 1 0 1 0 0 0
X₂ 0 1 -1 1 0 0 0 0 0 0
X₃ 0 0 0 -1 -1 1 0 1 0 0
X₄ 0 0 0 0 0 0 -1 -1 1 0
X₅ 0 0 0 0 0 0 0 0 -1 -1
X₆ 0 0 0 0 0 -1 0 0 0 1

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₇.

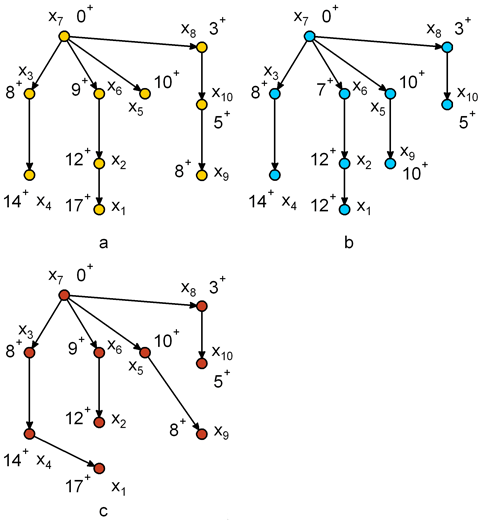
На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна. v_n=∑ a_i / ∑ b_i

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 4.

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин E и B

Какого типа граф изображен на рисунке?

Является ли граф, представленный на рисунке, планарным?

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₁и х₂,

Найти прямые отображения для вершин х₅ и х₆графа, показанного на рисунке

Является ли граф, изображенный на рисунке орграфом?

Какие вершины инцидентны дуге d в графе на рисунке?

Какие дуги инцидентны вершине 1 в графе на рисунке?

Найдите полустепени исхода и захода для вершины х₁ (вершина обзначена на рисунке цифрой 1) графа

Для графа, изображенного на рисунке, дать описание с помощью отображений

Для графа, представленного на рисунке, данаматрица инциденций. Верно ли представлен граф?
матрица инциденций
a₁ a₂ a₃ a₄ a₅ a₆ a₇
X₁ 0 1 1 0 0 0 -1
X₂ 0 -1 0 -1 1 0 0
X₃ 0 0 0 0 -1 -1 0
X₄ 0 0 -1 1 0 1 1

По матрице смежности, данной ниже подсчитать полустепень исхода второй вершины d_o(х₂)
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

Соответствует ли матрица инциденций матрице смежности (обе матрицы представлены ниже):
матрица инциденций
a₁ a₂ a₃ a₄ a₅ a₆ a₇ a₈ a₉ a₁₀
X₁ 1 -1 1 0 1 0 1 0 0 0
X₂ 0 1 -1 1 0 0 0 0 0 0
X₃ 0 0 0 -1 -1 1 0 1 0 0
X₄ 0 0 0 0 0 0 -1 -1 1 0
X₅ 0 0 0 0 0 0 0 0 -1 -1
X₆ 0 0 0 0 0 -1 0 0 0 1
матрица смежности
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 1 1 1 1 0 0
X₂ 1 0 1 0 0 0
X₃ 0 0 0 1 0 1
X₄ 0 0 0 0 1 0
X₅ 0 0 0 0 0 0
X₆ 0 0 0 0 1 0

Выполнить операцию нахождения кольцевой суммы G₁ G₂ для графов, показанных на рисунке 1

Выполнить операцию объединения G₁ ∪ G₂ для графов, представленных матрицами смежности в таблице 1
Матрица смежности G1
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 1 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 1 0 1 0
Матрица смежности G2
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 0 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 0 0 0 0
a
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 0 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 0 0 0 0
б
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 0
X₂ 0 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 0 0 1
X₅ 0 1 0 1 0
в
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 1 0 1 0

Для графа G₁, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х₃,х₄). Верно ли результат представлен на рис. 2а?

Для графа G₂, показанном на рисунке 1, выполнить операцию стягивания двух вершин (х₃,х₄). Верно ли результат представлен матрицей смежности ниже?
X₁ X₂ X_(3,4) X₅
X₁ 1
X₂ 1 1 1
X_(3,4) 1 1
X₅

В графе G₆ , показанном на рис. 1 удалить дугу (х₃,х₂). Результат представлен в матричном виде ниже
а
X₁ X₂ X₃
X₁ 1 1
X₂ 1 1
X₃ 1
б
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1
в
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1

Найти прямые отображения для вершин х₃ и х₄ графа, показанного на рисунке

Найти обратные отображения для вершин х₃ и х₄ графа, показанного на рисунке

Найти прямые многозначные отображения 3-го порядка для вершин х₅ и х₆ графа, показанного на рисунке

Найти обратные многозначные отображения 4-го порядка для вершин х₁ и х₂ графа, показанного на рисунке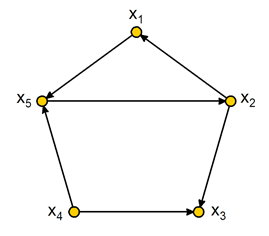

Для графа, представленного на рисунке 1 построить матрицу достижимости R
а
X₁ X₂ X₃ X₄ X₅
X₁ 1 1 1 1 1
R= X₂ 0 0 1 1 1
X₃ 0 0 1 1 0
X₄ 0 0 0 1 0
X₅ 0 0 0 1 1
б
X₁ X₂ X₃ X₄ X₅
X₁ 1 1 1 1 1
R= X₂ 0 0 1 1 1
X₃ 0 0 0 1 0
X₄ 0 0 0 0 0
X₅ 0 0 0 1 0
в
X₁ X₂ X₃ X₄ X₅
X₁ 1 1 1 1 1
R= X₂ 0 1 1 1 1
X₃ 0 0 1 1 0
X₄ 0 0 0 1 0
X₅ 0 0 0 1 1

Какая из представленных матриц контрдостижимости соответствует графу на рис. 1?
а
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 0 0 0 1 1 1
Q= X₂ 1 0 1 1 1 1
X₃ 1 0 0 1 1 1
X₄ 1 0 0 0 1 1
X₅ 1 0 0 1 0 1
X₆ 1 0 0 1 1 0
б
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 1 0 0 1 1 1
Q= X₂ 1 1 1 1 1 1
X₃ 1 0 1 1 1 1
X₄ 1 0 0 1 1 1
X₅ 1 0 0 1 1 1
X₆ 1 0 0 1 1 1
в
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 1 1 1 1 1 1
Q= X₂ 0 1 0 0 0 0
X₃ 0 1 1 0 0 0
X₄ 1 1 1 1 1 1
X₅ 1 1 1 1 1 1
X₆ 1 1 1 1 1 1

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х₁и х₃.

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 2.

Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: A и C или B и D

Для графа, данного на рисунке найти количество путей длиной 4 между всеми вершинами графа

По матрицам смежности определить какие из графов являются полными.
а
1 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
b
0 1 0 1
0 0 0 1
0 0 1 0
1 0 1 0
c
1 0 1 0
1 1 0 1
0 1 1 1
0 1 1 1
d
1 0 1 0
1 1 0 0
0 1 1 0
1 0 1 0

Какие из приведенных на рисунке графов являются симметрическими?

Какие из приведенных на рисунке графов являются антисимметрическими?

Какие из приведенных на рисунке графов являются деревьями?

Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его остовными подграфами?

Для графа G = (X, A), представленного на рисунке 1, описать матрицей смежности порожденный подграф {х₁,х₂,х₃,х₄,х₅}
а
X₁ X₂ X₃ X₄ X₅
X₁ 0 1 0 0 0
X₂ 0 0 1 0 1
X₃ 0 0 0 0 1
X₄ 0 0 1 0 0
X₅ 0 0 1 0 0
b
X₁ X₂ X₃ X₄ X₅
X₁ 0 1 0 0 0
X₂ 0 0 1 0 1
X₃ 0 0 0 1 1
X₄ 0 0 0 1 0
X₅ 0 0 1 1 0
c
X₁ X₂ X₃ X₄ X₅
X₁ 0 1 0 0 0
X₂ 0 0 1 0 1
X₃ 0 0 0 1 1
X₄ 0 0 0 0 0
X₅ 0 0 1 0 0

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈ A' тогда и только тогда, когда i+j нечетно

Выделить в графе на рисунке с сильную компоненту, содержащую максимальное число элементов.

Выделить в графе на рисунке а одностороннюю компоненту, содержащую максимальное число элементов.

Для графа на рисунке найти сильную компоненту, содержащую элемент х₄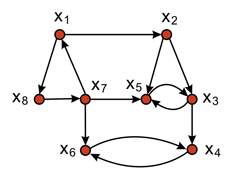

Методом Мальгранжа разбить граф, представленный на рисунке, на максимальные сильно связные подграфы

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин A и E.

Построить орцепи максимальной длины из вершин D и B графа, изображенного на рисунке

Построить простые орцепи максимальной длины из вершин A и D графа, изображенного на рисунке

Для графа на рисунке даны маршруты из вершины A в вершину F:
a) (A, B), (B, C), (C, G), (G, F)

b) (A, K), (K, H), (H, F)

c) (A, C), (C, E), (E, D), (D, C), (C, H), (H, F)

d) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

Найти среди них цепи

Для графа, представленного на рисунке даны замкнутые пути:

М₁: (х₂, х₃), (х₃, х₄), (х₄, х₇), (х₇, х₂)

М₂: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂) (х₂, х₃), (х₃, х₇), (х₇, х₂)

М₃: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂)

М₄: (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₃)

М₅: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₁)

М₆: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆) (х₆, х₁)

М₇: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆), (х₆, х₁), (х₁, х₂)

Какие из этих путей являются гамильтоновыми контурами?

Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы.

Обновление пометок на каждой итерации алгоритма Дейкстры происходит

Если с помощью алгоритма Дейкстры требуется найти кратчайшие пути от вершины x3 до других вершин графа, то в первой итерации ей присваивается пометка со значением ...

Найти кратчайший путь от вершины 1 к вершине 6 графа, представленного на рисунке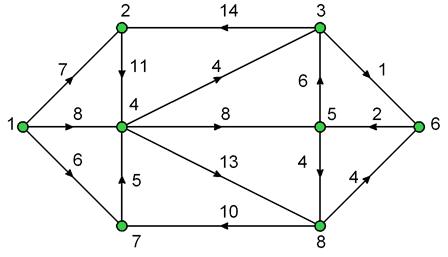

Найти кратчайший путь от вершины x₁ к вершине x₉ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₁.

Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного матрицей смежности
X₁ X₂ X₃ X₄ X₅ X₆ X₇ X₈
X₁ 1 1 1 0 0 0 0 0
X₂ 1 0 1 0 0 0 1 0
X₃ 0 0 0 0 1 0 0 0
X₄ 0 0 1 1 0 0 0 0
X₅ 0 0 0 1 1 0 0 0
X₆ 0 0 0 0 0 1 0 0
X₇ 0 1 0 0 0 1 0 1
X₈ 1 0 1 0 1 0 0 0

Найти обратные отображения для вершин х₁и х₂графа, показанного на рисунке

Какие из приведенных на рисунке графов являются симметрическими?

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈ A' тогда и только тогда, когда i+j < 10

Для графа G₂, показанном на рисунке a, выполнить операцию стягивания двух вершин (х₃,х₄). Верно ли результат представлен графом на рисунке б?

Какие из приведенных на рисунке графов являются антисимметрическими?

Для графа на рисунке найти сильную компоненту, содержащую элемент х₅

Для графа G₁, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х₁,х₂). Верно ли результат представлен матрицей смежности ниже?
X_(1,2) X₃ X₄ X₅
X_(1,2) 1 1 1
X₃
X₄ 1
X₅ 1 1

Для графа, представленного на рисунке даны замкнутые пути:

М₁: (х₂, х₃), (х₃, х₄), (х₄, х₇), (х₇, х₂)

М₂: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂) (х₂, х₃), (х₃, х₇), (х₇, х₂)

М₃: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂)

М₄: (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₃)

М₅: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₁)

М₆: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆) (х₆, х₁)

М₇: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆), (х₆, х₁), (х₁, х₂)

Какие из этих путей являются контурами?

Какие из приведенных на рисунке графов являются полными?

Для графа, представленного на рисунке построить матрицу контрдостижимости и определить какая из вершин достижима для наибольшего числа вершин графа.

По матрице смежности, данной ниже подсчитать полустепень захода второй вершины d_t(х₂)
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

Какие вершины инцидентны дуге f в графе на рисунке?

По матрицам смежности, приведенным ниже определить какие из графов являются полными.
а
1 1 1 1
0 0 1 1
0 0 0 1
1 1 1 1
b
0 1 0 1
0 0 0 1
0 0 1 0
1 0 1 0
c
1 0 1 1
1 1 0 1
0 1 1 1
1 1 1 1
d
0 0 0 0
1 0 0 0
1 1 0 0
1 1 1 0

Для графа, представленного на рисунке построить гамильтонов цикл и эйлеров путь.

Какие из приведенных на рисунке графов являются полными симметрическими?

По матрице инциденций найти полустепени исхода для Х₂
a₁ a₂ a₃ a₄ a₅ a₆ a₇ a₈ a₉ a₁₀
X₁ 1 -1 1 0 1 0 1 0 0 0
X₂ 0 1 -1 1 0 0 0 0 0 0
X₃ 0 0 0 -1 -1 1 0 1 0 0
X₄ 0 0 0 0 0 0 -1 -1 1 0
X₅ 0 0 0 0 0 0 0 0 -1 -1
X₆ 0 0 0 0 0 -1 0 0 0 1

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х₁ и х₂,

Какие из приведенных на рисунке графов являются односторонне связными?

Для чего использую алгоритм Дейкстра?

Является ли граф, представленный на рисунке, планарным?

В графе G₆ , показанном на рис. 1 удалить дугу (х₁,х₂). Результат представлен ниже в матричном виде
а
X₁ X₂ X₃
X₁ 1 1
X₂ 1 1
X₃ 1
б
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1
в
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х₁ и х₇.

Для графа, данного на рисунке найти количество путей длиной 3 между всеми вершинами графа.

Для графа, изображенного на рисунке, дать описание перечислением.

Какая из представленных матриц достижимости соответствует графу на рисунке 1?
а
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 0 0 0 1 1 1
R= X₂ 1 0 1 1 1 1
X₃ 1 0 0 1 1 1
X₄ 1 0 0 0 1 1
X₅ 1 0 0 1 0 1
X₆ 1 0 0 1 1 0
б
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 1 0 0 1 1 1
R= X₂ 1 1 1 1 1 1
X₃ 1 0 1 1 1 1
X₄ 1 0 0 1 1 1
X₅ 1 0 0 1 1 1
X₆ 1 0 0 1 1 1
в
X₁ X₂ X₃ X₄ X₅ X₆
X₁ 1 1 1 1 1 1
R= X₂ 0 1 0 0 0 0
X₃ 0 1 1 0 0 0
X₄ 1 1 1 1 1 1
X₅ 1 1 1 1 1 1
X₆ 1 1 1 1 1 1

Для нахождения кратчайшего пути от s к х_i, предшествующую вершину x_i^* можно найти как одну из вершин, для которой

Найти кратчайший путь от вершины 1 к вершине 8 графа, представленного на рисунке

Какие дуги инцидентны вершине 3 в графе на рисунке?

Выполнить операцию нахождения кольцевой суммы G₁ ⊕ G₂ для графов, представленных матрицами смежности в таблице 1
Матрица смежности G1
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 1 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 1 0 1 0
Матрица смежности G2
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 0 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 0 0 0 0
a
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 0 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 0 0 0 0
б
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 0
X₂ 0 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 0 0 1
X₅ 0 1 0 1 0
в
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 1 0 1 0

Найти прямые многозначные отображения 4-го порядка для вершин х₁ и х₂ графа, показанного на рисунке

Найти обратные многозначные отображения 3-го порядка для вершин х₃и х₄графа, показанного на рисунке

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₅и х₆,

Для графа, данного на рисунке найти количество путей длиной 2 между всеми вершинами графа.

Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: F и C или E и C

Какие из приведенных на рисунке графов являются полными?

Какие из приведенных на рисунке графов являются симметрическими?

Является ли граф на рисунке двудольным?

Дан граф на риунке 1. Какой из приведенных на рисунке 2 графов является для него порожденным подграфом?

Для графа G = (X, A) , представленного на рисунке 1, описать матрицей смежности порожденный подграф {х₂,х₃, х₄,х₅, х₆}
а
X₂ X₃ X₄ X₅ X₆
X₂ 0 1 0 1 0
X₃ 0 0 1 1 0
X₄ 0 0 0 0 1
X₅ 0 1 0 0 0
X₆ 0 0 1 0 0
b
X₂ X₃ X₄ X₅ X₆
X₂ 0 1 0 0 0
X₃ 0 0 1 1 0
X₄ 0 0 1 0 0
X₅ 0 0 0 1 0
X₆ 1 0 0 1 0
c
X₂ X₃ X₄ X₅ X₆
X₂ 0 1 0 0 0
X₃ 0 0 1 0 1
X₄ 0 0 0 0 1
X₅ 0 1 0 0 1
X₆ 1 0 1 0 0

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈X тогда и только тогда, когда i+j четно

Выделить в графе на рисунке f сильную компоненту, содержащую максимальное число элементов.

Методом Мальгранжа разбить граф, представленный на рисунке, на подграфы

Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного матрицей смежности
X₁ X₂ X₃ X₄ X₅ X₆ X₇ X₈
X₁ 1 1 0 1 0 0 0 0
X₂ 1 0 1 0 1 0 1 0
X₃ 0 0 0 0 1 0 0 0
X₄ 0 0 1 1 0 0 0 0
X₅ 0 0 0 1 1 0 0 0
X₆ 0 0 0 0 0 1 0 0
X₇ 0 1 1 0 0 1 0 1
X₈ 1 0 0 0 0 0 0 1

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин A и D.

Для графа на рисунке даны маршруты из вершины A в вершину F:
a) (A, B), (B, C), (C, G), (G, F)

b) (A, K), (K, H), (H, F)

c) (A, C), (C, E), (E, D), (D, C), (C, H), (H, F)

d) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

Найти среди них простые цепи

На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна.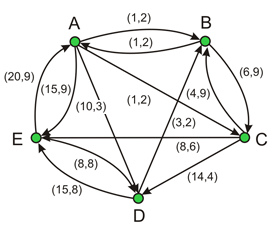

Скорость оборота капитала n -го пути судна найдем как суммарную выгоду пути, деленную на суммарное время, т. е.

v_n=∑ a_i/ ∑ b_i
A → B → C → D → E → A
A → B → C → E → D → A.
A → D → B → C → E → A.
A → C → E → D → B → A.

Значение постоянной метки показывает

Найти кратчайший путь от вершины x₁ к вершине x₅ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис.Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₃.

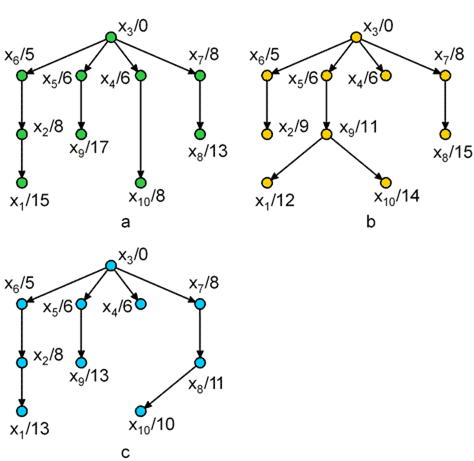
Для графа G₂, показанном на рисунке 1, выполнить операцию стягивания двух вершин (х₁,х₂). Верно ли результат представлен матрицей смежности ниже?
X_(1,2) X₃ X₄ X₅
X_(1,2) 1 1
X₃
X₄ 1 1 1
X₅

По матрице смежности, данной ниже подсчитать количество петель графа.
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: F и C или D и B

Перечислите дуги, являющиеся петлями в графе на рисунке?

Какие дуги инцидентны вершине 2 в графе на рисунке?

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₃ и х₄

Найти максимальный сильно связанный подграф, включающий вершину F, для графа, матрица смежности которого представлена ниже
A B C D E F G K
A 1 1 0 0 1 0 0 0
B 0 0 1 0 1 1 0 0
C 0 0 1 0 1 0 0 0
D 0 0 0 0 0 0 0 1
E 0 0 0 0 0 1 0 0
F 1 0 0 0 0 0 1 0
G 0 0 0 0 0 0 0 1
K 0 0 0 1 0 0 0 0

Найти прямые многозначные отображения 2-го порядка для вершин х₃ и х₄ графа, показанного на рисунке

Даны матрицы смежности и матрица инцидентности. Соответствуют ли они графу на рисунке?
матрица смежности
X₁ X₂ X₃ X₄
X₁ 1 1 0 0
X₂ 0 0 1 1
X₃ 0 0 0 0
X₄ 1 1 1 0
матрица инциденций
a₁ a₂ a₃ a₄ a₅ a₆ a₇
X₁ 0 1 1 0 0 0 -1
X₂ 0 -1 0 -1 1 0 0
X₃ 0 0 0 0 -1 -1 0
X₄ 0 0 -1 1 0 1 1

Найти обратные отображения для вершин х₅и х₆графа, показанного на рисунке

Является ли граф, изображенный на рисунке смешанным графом?

Какие вершины инцидентны дуге b в графе на рисунке?

Какие дуги являются петлями в графе на рисунке?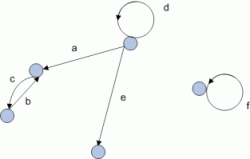

Для графа, изображенного на рисунке, дано описание с помощью отображений. G = (X, Г) , где X = {х_i}, i = 1, 2, 3, 4 – множество вершин, Г(х₁)= , Г(х₂) ={ х₁, х₄ }, Г(х₃) = { х₁, х₃ }, Г(х₄) = { х₁ } – отображения. Верно ли оно?

Выполнить операцию пересечения G₁ ∩ G₂ для графов, представленных матрицами смежности в таблице 1
Матрица смежности G1
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 1 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 1 0 1 0
Матрица смежности G2
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 0 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 0 0 0 0
a
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 0 0 0
X₃ 0 0 0 0 0
X₄ 0 0 1 0 0
X₅ 0 0 0 0 0
б
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 0
X₂ 0 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 0 0 1
X₅ 0 1 0 1 0
в
X₁ X₂ X₃ X₄ X₅
X₁ 0 0 0 0 1
X₂ 1 0 1 1 1
X₃ 0 0 0 0 0
X₄ 0 1 1 0 1
X₅ 0 1 0 1 0

Для графа G₁, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х₃,х₄). Верно ли результат представлен матрицей смежности ниже?
X₁ X₂ X_(3,4) X₅
X₁ 1
X₂ 1
X_(3,4) 1
X₅ 1 1

Для графа, представленного на рисунке построить матрицу достижимости и определить для какой из вершин графа достижимо наибольшее число вершин.

Какие из приведенных на рисунке графов являются полными симметрическими?

Является ли граф на рисунке двудольным?

Для графа G = (X, A) , представленного на рисунке 1, описать матрицей смежности порожденный подграф {х₁,х₂,х₃, ,х₅, х₇}
а
X₁ X₂ X₃ X₅ X₇
X₁ 0 1 0 0 0
X₂ 0 0 1 0 1
X₃ 0 0 0 0 1
X₅ 0 0 1 0 0
X₇ 0 0 1 0 0
b
X₁ X₂ X₃ X₅ X₇
X₁ 0 1 0 0 0
X₂ 0 0 1 1 0
X₃ 0 0 0 1 0
X₅ 0 0 1 0 0
X₇ 1 0 0 1 0
c
X₁ X₂ X₃ X₅ X₇
X₁ 0 1 0 0 0
X₂ 0 0 1 0 1
X₃ 0 0 0 1 1
X₅ 0 0 0 0 1
X₇ 1 0 1 0 0

Выделить в графе на рисунке e сильную компоненту, содержащую максимальное число элементов.

Выделить в графе на рисунке b одностороннюю компоненту, содержащую максимальное число элементов.

Для графа на рисунке найти сильную компоненту, содержащую элемент х₁

Методом Мальгранжа разбить граф, представленный ниже матрицей смежности, на подграфы
X₁ X₂ X₃ X₄ X₅ X₆ X₇ X₈
X₁ 1 1 0 1 0 0 0 0
X₂ 1 0 1 0 0 0 1 0
X₃ 0 0 0 0 1 0 0 0
X₄ 0 0 1 0 0 0 0 0
X₅ 0 0 0 1 0 0 0 0
X₆ 0 0 0 0 0 0 0 0
X₇ 0 1 0 0 0 1 0 1
X₈ 1 0 0 0 0 0 0 0

Построить орцепи максимальной длины из вершин E и F графа, изображенного на рисунке

В графе G₆ , показанном на рис. 1 удалить дугу (х₁,х₃). Результат представлен ниже в матричном виде
а
X₁ X₂ X₃
X₁ 1 1
X₂ 1 1
X₃ 1
б
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1
в
X₁ X₂ X₃
X₁ 1
X₂ 1 1
X₃ 1 1

Для графа на рисунке даны маршруты из вершины A в вершину F:

a) (A, B), (B, C), (C, F)

b) (A, K), (K, H), (H, F)

c) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

Найти среди них цепи

В графе G₆ , показанном на рис. 1 удалить вершину х₂. Результат представлен в матричном виде ниже
а
X₂ X₃
X₂ 0 1
X₂ 1 0
б
X₁ X₂
X₁ 0 1
X₂ 1 0
в
X₁ X₃
X₁ 0 1
X₃ 1 0

По матрицам смежности определить какие из графов являются полными.
а
1 1 1 1 0
0 1 0 1 0
0 0 1 1 0
0 0 0 1 0
1 1 1 1 0
b
0 1 0 1 0
0 0 0 1 1
1 1 0 0 0
0 0 1 0 1
1 0 1 0 0
c
1 1 0 1 1
1 1 1 0 1
0 1 1 1 1
1 0 1 1 1
1 1 1 1 1
d
0 0 0 0 0
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0

Какие из приведенных на рисунке графов являются полными антисимметрическими?

Является ли граф, представленный на рисунке, планарным?

Выделить в графе на рисунке f одностороннюю компоненту, содержащую максимальное число элементов.

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х₁ и х₆.

Найдите полустепени исхода и захода для вершины х₂ графа

Выполнить операцию объединения G₁ G₂ для графов, показанных на рисунке 1

Для графа G₁, показанном на рисунке a, выполнить операцию стягивания двух вершин (х₁,х₂). Верно ли результат представлен графом на рисунке б?

Найти прямые отображения для вершин х₁ и х₂ графа, показанного на рисунке

На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна. v_n=∑ a_i/ ∑ b_i

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х₃ и х₄

В графе G₆ , показанном на рис. 1 удалить вершину х₃. Результат представлен в матричном виде ниже
а
X₂ X₃
X₂ 0 1
X₂ 1 0
б
X₁ X₂
X₁ 0 1
X₂ 1 0
в
X₁ X₃
X₁ 0 1
X₃ 1 0

Построить простые орцепи максимальной длины из вершин F и E графа, изображенного на рисунке

Какие из приведенных на рисунке графов являются сильно связными?

Найти обратные многозначные отображения 4-го порядка для вершин х₅ и х₃графа, показанного на рисунке

Найти максимальный сильно связанный подграф, включающий вершину Е, для графа, матрица смежности которого представлена ниже
A B C D E F G K
A 1 1 0 0 1 0 0 0
B 0 0 1 0 1 1 0 0
C 0 0 1 0 1 0 0 0
D 0 0 0 0 0 0 0 1
E 0 0 0 0 0 1 0 0
F 1 0 0 0 0 0 1 0
G 0 0 0 0 0 0 0 1
K 0 0 0 1 0 0 0 0

Методом Мальгранжа разбить граф, представленный на рисунке, на максимальные сильно связные подграфы

Для графа, представленного на рисунке даны замкнутые пути:

М₁: (х₂, х₃), (х₃, х₄), (х₄, х₇), (х₇, х₂)

М₂: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂) (х₂, х₃), (х₃, х₇), (х₇, х₂)

М₃: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₂)

М₄: (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₃)

М₅: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₆), (х₆, х₁)

М₆: (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆) (х₆, х₁)

М₇: (х₂, х₃), (х₃, х₄), (х₄, х₅), (х₅, х₇), (х₇, х₆), (х₆, х₁), (х₁, х₂)

Какие из этих путей являются эйлеровыми контурами?

Найти кратчайший путь от вершины 1 к вершине 5 графа, представленного на рисунке

Введение в теорию графов - ответы

Какие дуги являются петлями в графе на рисунке?

Выполнить операцию пересечения G1 G2 для графов, показанных на рисунке 1

Методом Мальгранжа разбить граф, представленный матрицей смежности, на максимальные сильно связные подграфыX1X2X3X4X5X6X7X8X101000001X210101000X300011000X400000100X500100010X600010000X710001100X800000010

Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы.

Какие из приведенных на рисунке графов являются полными?

Для графа, представленного на рисунке, данаматрица смежности. Верно ли представлен граф?матрица смежностиX1X2X3X4X11100X20011X30000X41110

Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного на рисунке

Найдите полустепени исхода и захода для вершины х3 графа

Является ли граф на рисунке двудольным

Обновление пометок происходит по формуле:

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 3.

Для графа, приведенного на рисунке 1, найти матрицу контрдостижимости. аX1X2X3X4X5X110000Q=X211000X311100X410111X511001бX1X2X3X4X5X110000Q=X211000X311100X411111X511001вX1X2X3X4X5X110000Q=X211000X311100X411110X511001

Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его подграфами?

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х5и х6,

В графе G6 , показанном на рис. 1 удалить вершину х1. Результат представлен ниже в матричном виде аX2X3X201X310бX1X2X101X210вX1X3X101X310

Какие из приведенных на рисунке графов являются слабо связными?

Методом Мальгранжа разбить граф, представленный ниже матрицей смежности, на подграфыX1X2X3X4X5X6X7X11101000X21010010X30000100X40010000X50001000X60100001X71000000

Найти кратчайший путь от вершины x1 к вершине x10 графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б

Построить орцепи максимальной длины из вершин A и B графа, изображенного на рисунке

Построить простые орцепи максимальной длины из вершин A и B графа, изображенного на рисунке

По матрице инциденций найти полустепени захода для Х2 a1a2a3a4a5a6a7a8a9a10X12-110101000X201-11000000X3000-1-110100X4000000-1-110X500000000-1-1X600000-10001

Для графа, представленного на рисунке 1а, построить базу относительно вершины х7.

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 4.

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вер­шин E и B

Какого типа граф изображен на рисунке?

Является ли граф, представленный на рисунке, планарным?

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х1и х2,

Найти прямые отображения для вершин х5 и х6графа, показанного на рисунке

Является ли граф, изображенный на рисунке орграфом?

Какие вершины инцидентны дуге d в графе на рисунке?

Какие дуги инцидентны вершине 1 в графе на рисунке?

Найдите полустепени исхода и захода для вершины х1 (вершина обзначена на рисунке цифрой 1) графа

Для графа, изображенного на рисунке, дать описание с помощью отображений

Для графа, представленного на рисунке, данаматрица инциденций. Верно ли представлен граф?матрица инциденцийa1a2a3a4a5a6a7X1011000-1X20-10-1100X30000-1-10X400-11011

По матрице смежности, данной ниже подсчитать полустепень исхода второй вершины do(х2) 101100010101000101001001100000010001

Выполнить операцию нахождения кольцевой суммы G1 G2 для графов, показанных на рисунке 1

Для графа G1, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х3,х4). Верно ли результат представлен на рис. 2а?

Для графа G2, показанном на рисунке 1, выполнить операцию стягивания двух вершин (х3,х4). Верно ли результат представлен матрицей смежности ниже? X1X2X(3,4)X5X11X2111X(3,4)11X5

В графе G6 , показанном на рис. 1 удалить дугу (х3,х2). Результат представлен в матричном виде ниже аX1X2X3X111X211X31бX1X2X3X11X211X311вX1X2X3X11X211X311

Найти прямые отображения для вершин х3 и х4 графа, показанного на рисунке

Найти обратные отображения для вершин х3 и х4 графа, показанного на рисунке

Найти прямые многозначные отображения 3-го порядка для вершин х5 и х6 графа, показанного на рисунке

Найти обратные многозначные отображения 4-го порядка для вершин х1 и х2 графа, показанного на рисунке

Для графа, представленного на рисунке 1 построить матрицу достижимости R аX1X2X3X4X5X111111R=X200111X300110X400010X500011бX1X2X3X4X5X111111R=X200111X300010X400000X500010вX1X2X3X4X5X111111R=X201111X300110X400010X500011

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х1и х3.

Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 2.

Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: A и C или B и D

Для графа, данного на рисунке найти количество путей длиной 4 между всеми вершинами графа

По матрицам смежности определить какие из графов являются полными.а1111001100010000b0101000100101010c1010110101110111d1010110001101010

Какие из приведенных на рисунке графов являются симметрическими?

Какие из приведенных на рисунке графов являются антисимметрическими?

Какие из приведенных на рисунке графов являются антисимметрическими?

Какие из приведенных на рисунке графов являются деревьями?

Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его остовными подграфами?

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где xi,xj ∈ A' тогда и только тогда, когда i+j нечетно

Выделить в графе на рисунке с сильную компоненту, содержащую максимальное число элементов.

Выделить в графе на рисунке а одностороннюю компоненту, содержащую максимальное число элементов.

Для графа на рисунке найти сильную компоненту, содержащую элемент х4

Методом Мальгранжа разбить граф, представленный на рисунке, на максимальные сильно связные подграфы

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин A и E.

Построить орцепи максимальной длины из вершин D и B графа, изображенного на рисунке

Построить простые орцепи максимальной длины из вершин A и D графа, изображенного на рисунке

Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы.

Обновление пометок на каждой итерации алгоритма Дейкстры происходит

Найти кратчайший путь от вершины 1 к вершине 6 графа, представленного на рисунке

Найти кратчайший путь от вершины x1 к вершине x9 графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х1.

Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного матрицей смежностиX1X2X3X4X5X6X7X8X111100000X210100010X300001000X400110000X500011000X600000100X701000101X810101000

Найти обратные отображения для вершин х1и х2графа, показанного на рисунке

Какие из приведенных на рисунке графов являются симметрическими?

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где xi,xj ∈ A' тогда и только тогда, когда i+j < 10

Для графа G2, показанном на рисунке a, выполнить операцию стягивания двух вершин (х3,х4). Верно ли результат представлен графом на рисунке б?

Какие из приведенных на рисунке графов являются антисимметрическими?

Для графа на рисунке найти сильную компоненту, содержащую элемент х5

Для графа G1, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х1,х2). Верно ли результат представлен матрицей смежности ниже? X(1,2)X3X4X5X(1,2)111X3X41X511

Какие из приведенных на рисунке графов являются полными?

Для графа, представленного на рисунке построить матрицу контрдостижимости и определить какая из вершин достижима для наибольшего числа вершин графа.

По матрице смежности, данной ниже подсчитать полустепень захода второй вершины dt(х2) 101100010101000101001001100000010001

Какие вершины инцидентны дуге f в графе на рисунке?

Выполнить операцию пересечения G₁ G₂ для графов, показанных на рисунке 1

Для графа, представленного на рисунке, данаматрица смежности. Верно ли представлен граф?
матрица смежности
X₁ X₂ X₃ X₄
X₁ 1 1 0 0
X₂ 0 0 1 1
X₃ 0 0 0 0
X₄ 1 1 1 0

Найдите полустепени исхода и захода для вершины х₃ графа

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х₅и х₆,

В графе G₆ , показанном на рис. 1 удалить вершину х₁. Результат представлен ниже в матричном виде
а
X₂ X₃
X₂ 0 1
X₃ 1 0
б
X₁ X₂
X₁ 0 1
X₂ 1 0
в
X₁ X₃
X₁ 0 1
X₃ 1 0

Найти кратчайший путь от вершины x₁ к вершине x₁₀ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₇.

Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин E и B

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₁и х₂,

Найти прямые отображения для вершин х₅ и х₆графа, показанного на рисунке

Найдите полустепени исхода и захода для вершины х₁ (вершина обзначена на рисунке цифрой 1) графа

По матрице смежности, данной ниже подсчитать полустепень исхода второй вершины d_o(х₂)
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

Выполнить операцию нахождения кольцевой суммы G₁ G₂ для графов, показанных на рисунке 1

Для графа G₁, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х₃,х₄). Верно ли результат представлен на рис. 2а?

Найти прямые отображения для вершин х₃ и х₄ графа, показанного на рисунке

Найти обратные отображения для вершин х₃ и х₄ графа, показанного на рисунке

Найти прямые многозначные отображения 3-го порядка для вершин х₅ и х₆ графа, показанного на рисунке

Найти обратные многозначные отображения 4-го порядка для вершин х₁ и х₂ графа, показанного на рисунке

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х₁и х₃.

По матрицам смежности определить какие из графов являются полными.
а
1 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
b
0 1 0 1
0 0 0 1
0 0 1 0
1 0 1 0
c
1 0 1 0
1 1 0 1
0 1 1 1
0 1 1 1
d
1 0 1 0
1 1 0 0
0 1 1 0
1 0 1 0

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈ A' тогда и только тогда, когда i+j нечетно

Для графа на рисунке найти сильную компоненту, содержащую элемент х₄

Найти кратчайший путь от вершины x₁ к вершине x₉ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₁.

Найти обратные отображения для вершин х₁и х₂графа, показанного на рисунке

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈ A' тогда и только тогда, когда i+j < 10

Для графа G₂, показанном на рисунке a, выполнить операцию стягивания двух вершин (х₃,х₄). Верно ли результат представлен графом на рисунке б?

Для графа на рисунке найти сильную компоненту, содержащую элемент х₅

По матрице смежности, данной ниже подсчитать полустепень захода второй вершины d_t(х₂)
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

По матрицам смежности, приведенным ниже определить какие из графов являются полными.
а
1 1 1 1
0 0 1 1
0 0 0 1
1 1 1 1
b
0 1 0 1
0 0 0 1
0 0 1 0
1 0 1 0
c
1 0 1 1
1 1 0 1
0 1 1 1
1 1 1 1
d
0 0 0 0
1 0 0 0
1 1 0 0
1 1 1 0

Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х₁ и х₂,

Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х₁ и х₇.

Для нахождения кратчайшего пути от s к х_i, предшествующую вершину x_i^* можно найти как одну из вершин, для которой

Найти прямые многозначные отображения 4-го порядка для вершин х₁ и х₂ графа, показанного на рисунке

Найти обратные многозначные отображения 3-го порядка для вершин х₃и х₄графа, показанного на рисунке

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₅и х₆,

Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где x_i,x_j ∈X тогда и только тогда, когда i+j четно

Найти кратчайший путь от вершины x₁ к вершине x₅ графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис.Б

Для графа, представленного на рисунке 1а, построить базу относительно вершины х₃.

По матрице смежности, данной ниже подсчитать количество петель графа.
1 0 1 1 0 0
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 0 0 1
1 0 0 0 0 0
0 1 0 0 0 1

Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х₃ и х₄

Найти прямые многозначные отображения 2-го порядка для вершин х₃ и х₄ графа, показанного на рисунке

Найти обратные отображения для вершин х₅и х₆графа, показанного на рисунке

Для графа на рисунке найти сильную компоненту, содержащую элемент х₁