Пусть случайное событие определено так 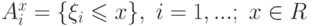 . Имеется
. Имеется 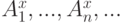 бесконечная последовательность событий. Тогда к чему
бесконечная последовательность событий. Тогда к чему 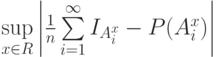 сходится почти наверное?
сходится почти наверное?
(Ответ необходимо ввести в поле ввода.)
Варианты ответа

 последовательность независимых событий:
последовательность независимых событий: 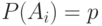 . Положим
. Положим 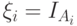 . Тогда к какой величине при
. Тогда к какой величине при 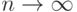 сходится
сходится  почти наверное?
почти наверное?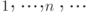 бесконечная последовательность независимых событий:
бесконечная последовательность независимых событий: 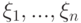 - последовательность независимых в совокупности случайных величин, для которых дисперсия конечна
- последовательность независимых в совокупности случайных величин, для которых дисперсия конечна 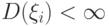 и сходится ряд
и сходится ряд 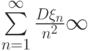 . С каким типом сходимости
. С каким типом сходимости 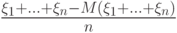 сходится к
сходится к  при
при 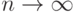 ?
? . Из множества
. Из множества  выбираем случайное подмножество
выбираем случайное подмножество  из
из  , где
, где ![m=\left[\frac{8d}{\epsilon} log_2 \frac{8d}{\epsilon} \right]](https://intuit.ru//sites/default/files/tex_cache/6049bf901b7724dca7ef621a2a8f67b5.png) по схеме выбора с возращением
по схеме выбора с возращением 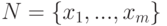 . Пусть определено событие
. Пусть определено событие 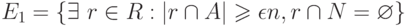 . Какое события является отрицанием события
. Какое события является отрицанием события 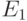 ?
?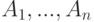 события, для каждого из которых выполнено
события, для каждого из которых выполнено 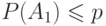 и любое событие
и любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук, причем и
штук, причем и  .Тогда ...
.Тогда ...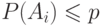 и любое событие
и любое событие  вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 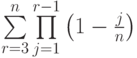 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) .При указанном интервале суммирования для
.При указанном интервале суммирования для 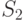 , что является нижней оценкой величины
, что является нижней оценкой величины 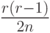 ?
?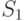 ?
?