Решите неоднородное уравнение 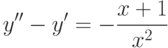 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 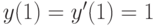 . В ответе укажите значение
. В ответе укажите значение  .
.
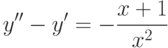
(Отметьте один правильный вариант ответа.)
Варианты ответа
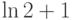 (Верный ответ)
(Верный ответ)
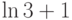

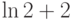
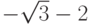
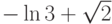

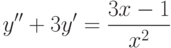
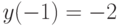 ,
, 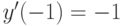 . В ответе укажите значение
. В ответе укажите значение 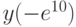 .
.
 ,
, 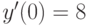 . В ответе укажите значение
. В ответе укажите значение  .
.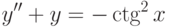
 ,
, 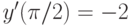 . В ответе укажите значение
. В ответе укажите значение  .
.
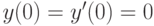 . В ответе укажите значение
. В ответе укажите значение 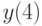 .
.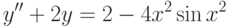
 .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
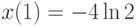 ,
,  . В ответе укажите значение
. В ответе укажите значение 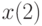 .
.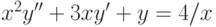 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям 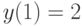 ,
, 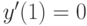 . В ответе укажите его значение
. В ответе укажите его значение 
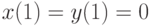 . В ответе укажите значение
. В ответе укажите значение 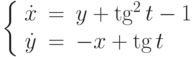
 . В ответе укажите значение
. В ответе укажите значение 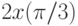 .
.