Вычислите определитель Вронского системы, состоящей из функций  и
и 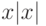 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(Отметьте один правильный вариант ответа.)
Варианты ответа
-1 да
0 да
1 нет
-1 нет
0 нет(Верный ответ)
1 да

 ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми? ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми? ,
, 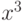 и
и 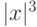 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?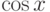 и
и 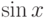 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?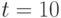 определителя Вронского двух вектор-функций
определителя Вронского двух вектор-функций 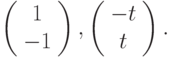
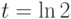 определителя Вронского двух вектор-функций
определителя Вронского двух вектор-функций 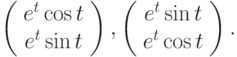
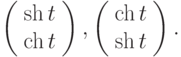
 уравнение вида
уравнение вида 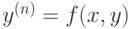 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции 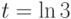 определителя Вронского трёх вектор-функций
определителя Вронского трёх вектор-функций 