Классические и квантовые вычисления

Какой функцией является перестановка на двух битах 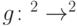$g\colon{} \cb^2\to \cb^2$ :

(Отметьте один правильный вариант ответа.)

Варианты ответа

нелинейной

обратимой

линейной(Верный ответ)

Похожие вопросы

Перестановка, реализуемая обратимой схемой, является ( $\calA$ - некоторое множество перестановок вида $G\colon\cb^k \to \cb^k$ ):

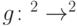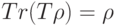Если имеется физически реализуемое преобразование $T\colon\LL(\calN)\to\LL(\calM)$ , причем для любого чистого состояния $\rho$ выполняется свойство: $Tr_{\calF}(T\rho)=\rho$ , то для любого оператора

справедливым является равенство ( $\gamma$ - некоторая фиксированная матрица плотности на пространстве $\calF$ ):

Если существует квантовый алгоритм вычисления функции $F\colon\cb^*\to\cb^*$ , работающий за время O(n^d)

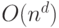для некоторой константы

, то функция $F\colon\cb^*\to\cb^*$

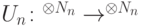Каким условиям должны удовлетворять операторы $U_n\colon \BB^{\otimes N_n}\to \BB^{\otimes N_n}$ , реализуемые однородной последовательностью квантовых схем полиномиального по

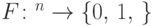размера, чтобы функция $F\colon \cb^n\to \{0,\,1,\,\}$ принадлежала классу BQNP:

Последовательность перестановок $U_1[A_1],\dots, U_l[A_l]$ , где A_j

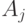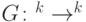- множества битов, $U_j\in\calA$ , $\calA$ - некоторое множество перестановок вида $G\colon\cb^k \to \cb^k$ является:

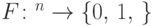Какому классу принадлежит функция $F\colon \cb^n\to \{0,\,1,\,\}$ , если существует однородная последовательность квантовых схем полиномиального по

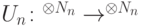размера, реализующих такие операторы $U_n\colon \BB^{\otimes N_n}\to \BB^{\otimes N_n}$ , что $F_n(x)=1 & \Longrightarrow & \exists\, \ket\xi\: \PP\Bigl(U_n\ket\xi\otimes\ket{x}\otimes\ket{0^{N_n-n-m_n}},\calM\Bigr) \geq p_1,\\ F_n(x)=0 & \Longrightarrow & \forall\, \ket\xi\: \PP\Bigl(U_n\ket\xi\otimes\ket{x}\otimes\ket{0^{N_n-n-m_n}},\calM\Bigr) \leq p_0.$

Функция $F\colon \cb^n\to \{0,\,1,\, \langle \text{не определено}\rangle}\}$ принадлежит классу NP, если есть частично определенная функция $R\in\P$ от двух переменных, такая что:

Для любого классического вероятностного алгоритма, делающего не более $2^{k/2}$ обращений к оракулу ( $n\geq k$ ), существует подгруппа $D\subseteq(\ZZ_2)^k$ и соответствующая функция $f\colon (\ZZ_2)^k\to\cb^n$ , для которой вероятность ошибки алгоритма:

Функция

является функцией полиномиального роста, если для некоторой константы

при достаточно больших

выполняется неравенство:

Что из перечисленного является характерным для тензорного произведения двух пространств

, в которых фиксированы базисы $\{e_1,\dots,e_l\}$ и $\{f_1,\dots,f_l\}$

Классические и квантовые вычисления

Какой функцией является перестановка на двух битах :

Какой функцией является перестановка на двух битах $g\colon{} \cb^2\to \cb^2$ :