Классические и квантовые вычисления

<<- Назад к вопросам

Как называются векторы из кодового подпространства являющиеся собственными и обладающие наименьшей энергией?

(Отметьте один правильный вариант ответа.)

Варианты ответа

основными состояниями(Верный ответ)

нет верного ответа

возбужденными состояниями

Похожие вопросы

Коэффициенты разложения по выделенному базису классических состояний называются:

Чему равна вероятность "события" $\calM$ для квантового состояния, задаваемого матрицей плотности $\rho$ и подпространства $\calM$ :

Почему

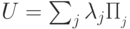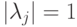в операторе $\Lambda(U)=\Pi_0\otimes I + \Pi_1\otimes U$ можно разложить в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ ?

Можно ли в операторе $\Lambda(U)=\Pi_0\otimes I + \Pi_1\otimes U$ разложить

в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ ?

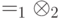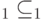Если на пространстве $\calN=\calN_1\otimes\calN_2$ задана матрица плотности вида $\rho_1\otimes\rho_2$ и имеется два подпространства $\calM_1\subseteq \calN_1$ , $\calM_2\subseteq \calN_2$ , то справедливо равентство:

Если унитарный оператор

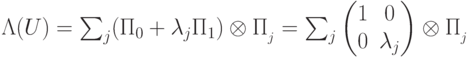разложить в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ , то $\Lambda(U)=\sum_{j} (\Pi_0+\lambda_j\Pi_1)\otimes\Pi_{\calL_j}= \sum_{j}^{} \begin{pmatrix} 1&0\\ 0&\lambda_j \end{pmatrix} \otimes\Pi_{\calL_j}$ . В этом случае условные вероятности будут равны:

Матрицы $\sx=\begin{pmatrix}0&1\\1&0\end{pmatrix},\; \sy=\leftp\begin{array}{rr}0&-i\\ i&0\end{array}\rightp,\; \sz=\leftp\begin{array}{rr}1&0\\0&-1\end{array}\rightp.$ , образующие ортонормированный базис, называются:

Если

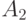- неотрицательные операторы, 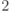$\calL_1$ , $\calL_2$ - их нулевые подпространства, причем 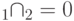$\calL_1\cap \calL_2=0$ , ненулевые собственные числа A_1

не меньше

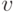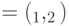, где $\vt=\vt(\calL_1,\calL_2)$ - угол между $\calL_1$ и $\calL_2$ , то справедливым является равенство:

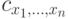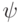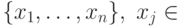Как называются коэффициенты $c_{x_1,\dots,x_n}$ разложения вектора $\ket{\psi}$ по базису $\{\ket{x_1,\dots,x_n}\}, \ x_j\in\cb$ :