Матрицы  , образующие ортонормированный базис, называются:
, образующие ортонормированный базис, называются:
(Отметьте один правильный вариант ответа.)
Варианты ответа
тензорными матрицами
матрицами Черча
матрицами Паули(Верный ответ)

 действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  соответствует повороту вокруг оси
соответствует повороту вокруг оси 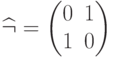 , то
, то  =:
=: разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 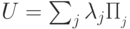 ,
,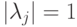 , то
, то 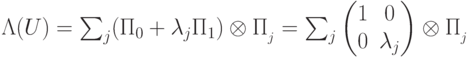 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны:
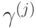 выступает в качестве:
выступает в качестве: - множество троек вида
- множество троек вида  , где
, где 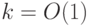 ,
, 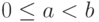 ,
, 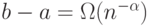 , (
, (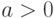 ), то для
), то для 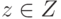 выполняются условия:
выполняются условия: , называется:
, называется: ,
, 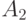 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 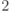 - их нулевые подпространства, причем
- их нулевые подпространства, причем 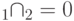 , ненулевые собственные числа
, ненулевые собственные числа 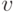 , где
, где 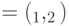 - угол между
- угол между  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
( - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 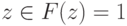 выполняется:
выполняется: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 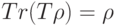 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): выполняется равенство:
выполняется равенство: