Классические и квантовые вычисления

<<- Назад к вопросам

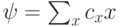Если система из q-битов находится в состоянии $\ket\psi=\sum_{x}^{}c_x\ket{x}$ , то вероятность обнаружить систему в состоянии x определяется как:

(Отметьте один правильный вариант ответа.)

Варианты ответа

(Верный ответ)

Похожие вопросы

Каким образом будут распределены классические состояния квантовой системы, находящейся в состоянии $\ket\psi=\sum_{x}^{}c_x\ket{x}$ :

Если

- множество троек вида $\langle\text{описание квантовой схемы } W\rangle, p_0, p_1)$ описанием схемы - приближенная реализация в стандартном базисе, а $p_1-p_0=\Omega(n^{-\alpha})$ ( a>0

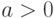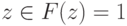- размер описания схемы). Тогда для $z\in\Z F(z)=1$ выполняется:

Если

- множество троек вида $(\langle\text{описание k-локального гамильтониана } H\rangle, a, b)$ , где k=O(1)

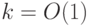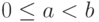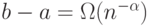, $0\leq a<b$ , $b-a=\Omega(n^{-\alpha})$ , ( a>0

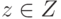), то для $z\in Z$ выполняются условия:

Условием алгоритма проверки простоты числа

, определяющим что

- составное, где

- случайное среди чисел от 1 до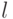

- нечетное, является:

Чему равна суммарная длина (F(x),z)

и $(x,O^{N-n})$ в формуле $\sum_{z}^{} \bigl| \langle F(x),z|\,U\,|x,0^{N-n}\rangle\bigr|^2 \geq \varepsilon$ , которой должна удовлетворять квантовая схема $U=U_L\cdot\ldots\cdot U_2U_1$ , вычисляющая

Если

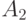- неотрицательные операторы, 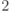$\calL_1$ , $\calL_2$ - их нулевые подпространства, причем 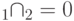$\calL_1\cap \calL_2=0$ , ненулевые собственные числа A_1

не меньше

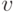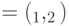, где $\vt=\vt(\calL_1,\calL_2)$ - угол между $\calL_1$ и $\calL_2$ , то справедливым является равенство:

Если вероятность правильного ответа для каждого экземпляра из

запущенных машин Тьюринга равна c>1/2

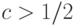, то вероятность правильного ответа после голосования

машин:

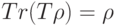Если имеется физически реализуемое преобразование $T\colon\LL(\calN)\to\LL(\calM)$ , причем для любого чистого состояния $\rho$ выполняется свойство: $Tr_{\calF}(T\rho)=\rho$ , то для любого оператора

справедливым является равенство ( $\gamma$ - некоторая фиксированная матрица плотности на пространстве $\calF$ ):

Если получено

дробей вида $k_1'/t_1',\,k_2'/t_2',\dots,k_l'/t_l'$ то вероятность того, что наименьшее общее кратное их знаменателей отлично от

(равномерно распределенное на множестве $\{0,\dots,t-1\}$ случайное число):

Если унитарный оператор

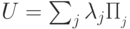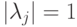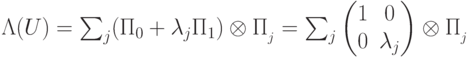разложить в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ , то $\Lambda(U)=\sum_{j} (\Pi_0+\lambda_j\Pi_1)\otimes\Pi_{\calL_j}= \sum_{j}^{} \begin{pmatrix} 1&0\\ 0&\lambda_j \end{pmatrix} \otimes\Pi_{\calL_j}$ . В этом случае условные вероятности будут равны:

Классические и квантовые вычисления

Если система из q-битов находится в состоянии , то вероятность обнаружить систему в состоянии x определяется как:

Если система из q-битов находится в состоянии $\ket\psi=\sum_{x}^{}c_x\ket{x}$ , то вероятность обнаружить систему в состоянии x определяется как: