Каким образом будут распределены классические состояния квантовой системы, находящейся в состоянии 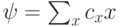 :
:
(Отметьте один правильный вариант ответа.)
Варианты ответа

 (Верный ответ)
(Верный ответ)


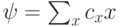 :
:
 (Верный ответ)
(Верный ответ)

 q-битов находится в состоянии
q-битов находится в состоянии 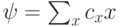 , то вероятность обнаружить систему в состоянии x определяется как:
, то вероятность обнаружить систему в состоянии x определяется как: разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 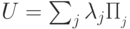 ,
,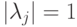 , то
, то 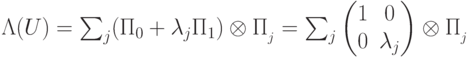 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны: - множество троек вида
- множество троек вида  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
(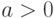 ,
,  - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 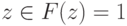 выполняется:
выполняется: в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 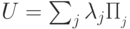 ,
,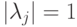 ?
? разложить
разложить  в сумму проекторов на собственные подпространства следующим образом:
в сумму проекторов на собственные подпространства следующим образом: 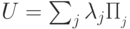 ,
,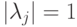 ?
? и
и  в формуле
в формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  :
: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 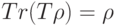 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
):