Как определяется слагаемое гамильтониана 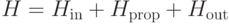 , отвечающее начальному состоянию:
, отвечающее начальному состоянию:
(Отметьте один правильный вариант ответа.)
Варианты ответа
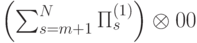 (Верный ответ)
(Верный ответ)



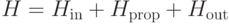 , отвечающее начальному состоянию:
, отвечающее начальному состоянию: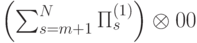 (Верный ответ)
(Верный ответ)


 , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: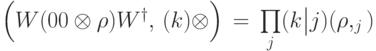 ?
? ,
, 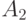 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 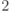 - их нулевые подпространства, причем
- их нулевые подпространства, причем 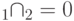 , ненулевые собственные числа
, ненулевые собственные числа  и
и 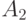 не меньше
не меньше 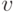 , где
, где 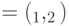 - угол между
- угол между  и
и 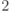 , то справедливым является равенство:
, то справедливым является равенство: - множество троек вида
- множество троек вида  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
(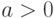 ,
,  - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 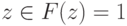 выполняется:
выполняется: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 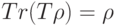 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
):