Если имеется действие  , то :
, то :
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
на ортогональном дополнении к подпространству, порожденному векторами 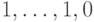 и
и 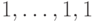 , действует тождественный оператор(Верный ответ)
, действует тождественный оператор(Верный ответ)
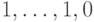 и
и 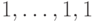 , действует тождественный оператор(Верный ответ)
, действует тождественный оператор(Верный ответ)
нет верного ответа
на подпространстве, порожденном векторами 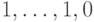 и
и 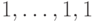 , действует оператор
, действует оператор 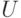 (Верный ответ)
(Верный ответ)
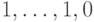 и
и 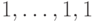 , действует оператор
, действует оператор 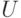 (Верный ответ)
(Верный ответ)

 , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 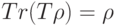 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): - множество троек вида
- множество троек вида  , где
, где 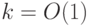 ,
, 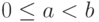 ,
, 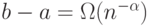 , (
, (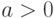 ), то для
), то для 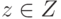 выполняются условия:
выполняются условия: , то разложение Шмидта имеет вид (
, то разложение Шмидта имеет вид (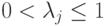 ,
, 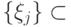 и
и 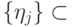 - ортонормированные вектора):
- ортонормированные вектора): ,
, 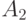 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 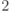 - их нулевые подпространства, причем
- их нулевые подпространства, причем 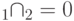 , ненулевые собственные числа
, ненулевые собственные числа 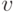 , где
, где 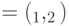 - угол между
- угол между  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
( - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 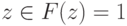 выполняется:
выполняется: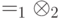 задана матрица плотности вида
задана матрица плотности вида  и имеется два подпространства
и имеется два подпространства 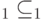 ,
,  , то справедливо равентство:
, то справедливо равентство: в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 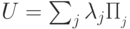 ,
,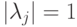 ?
?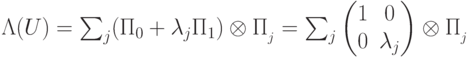 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны: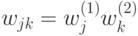 , имеется совместное распределение на множестве
, имеется совместное распределение на множестве 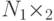 и событие не зависит от исхода во втором множестве
и событие не зависит от исхода во втором множестве 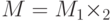 , то вероятность такого события выражается как:
, то вероятность такого события выражается как: