Какое будет ортогональное преобразование неизвестных для квадратичной формы 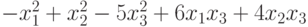 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
(Отметьте один правильный вариант ответа.)
Варианты ответа
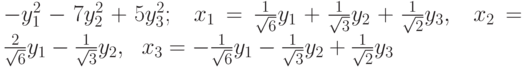
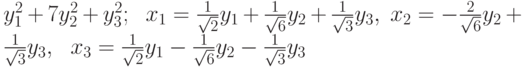
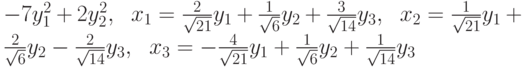

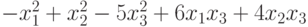 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?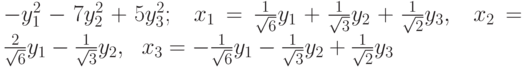
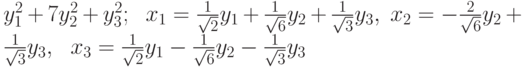
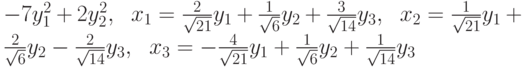
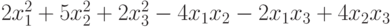 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?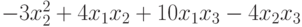 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?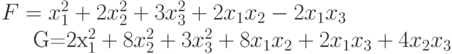 к каноническому виду?
к каноническому виду? к каноническому виду?
к каноническому виду?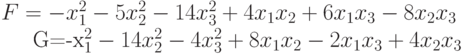
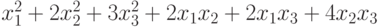 , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?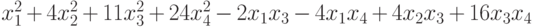 , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?