Как будет выглядеть невырожденное линейное преобразование, которое приводит квадратичные формы  к каноническому виду?
к каноническому виду?
(Отметьте один правильный вариант ответа.)
Варианты ответа
форма F отрицательно определена. Преобразование неизвестных  приводят форму F к нормальному виду, а форму G - к каноническому виду
приводят форму F к нормальному виду, а форму G - к каноническому виду 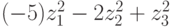
 приводят форму F к нормальному виду, а форму G - к каноническому виду
приводят форму F к нормальному виду, а форму G - к каноническому виду 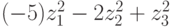
форма F положительно определена. Преобразование неизвестных 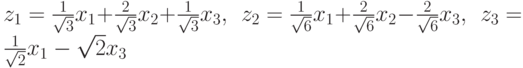 приводит форму F к нормальному виду, а форму G - к каноническому виду
приводит форму F к нормальному виду, а форму G - к каноническому виду 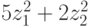
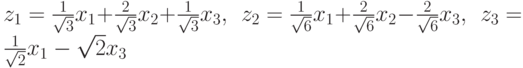 приводит форму F к нормальному виду, а форму G - к каноническому виду
приводит форму F к нормальному виду, а форму G - к каноническому виду 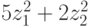
матрицы форм F и G перестановочны . Ортогональное преобразование неизвестных 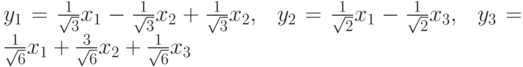 приводит форму к каноническуому виду
приводит форму к каноническуому виду  , а форму G - к каноническому виду
, а форму G - к каноническому виду 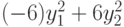 (Верный ответ)
(Верный ответ)
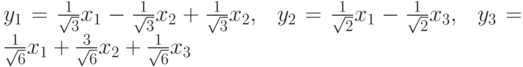
 , а форму G - к каноническому виду
, а форму G - к каноническому виду 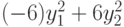 (Верный ответ)
(Верный ответ)

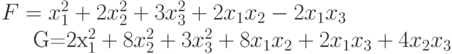 к каноническому виду?
к каноническому виду?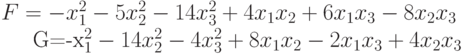
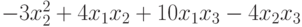 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?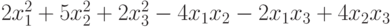 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?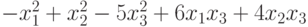 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?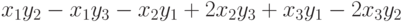 , если привести ее к каноническому виду?
, если привести ее к каноническому виду? в базисе
в базисе 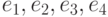 имеет матрицу
имеет матрицу 
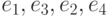 ?
?
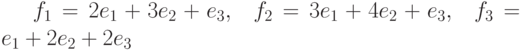 ?
? имеет матрицу
имеет матрицу 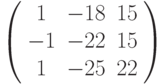
 ?
? - линейное преобразование пространства
- линейное преобразование пространства 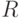 . Линейное подпространство
. Линейное подпространство 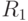 называется инвариантным относительно
называется инвариантным относительно