Какое доказательство, из ниже перечисленных, доказывает теорему:"Матрица проектора P в некотором базисе имеет вид 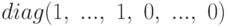 "?
"?
(Отметьте один правильный вариант ответа.)
Варианты ответа
если  , то
, то  .
.  состоит из векторов
состоит из векторов 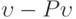 , т.е.
, т.е. 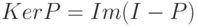 . Аналогично
. Аналогично  .
.
 , то
, то  .
.  состоит из векторов
состоит из векторов 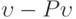 , т.е.
, т.е. 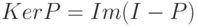 . Аналогично
. Аналогично  .
.
Выберем в пространстве W ортонормированный базис 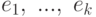 . Рассмотрим вектор
. Рассмотрим вектор 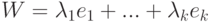 . Условие
. Условие  означает, что
означает, что 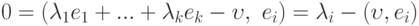 , т.е.
, т.е.  . Выбрав такие числа
. Выбрав такие числа 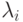 , получим требуемый вектор
, получим требуемый вектор  .
.
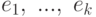 . Рассмотрим вектор
. Рассмотрим вектор 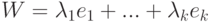 . Условие
. Условие  означает, что
означает, что 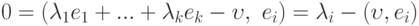 , т.е.
, т.е.  . Выбрав такие числа
. Выбрав такие числа 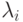 , получим требуемый вектор
, получим требуемый вектор  .
.
любой вектор 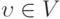 можно представить в виде
можно представить в виде 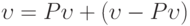 , где
, где  и
и 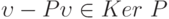 . Кроме того, если
. Кроме того, если 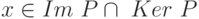 , то
, то  . В самом деле, тогда
. В самом деле, тогда 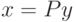 и
и  , поэтому
, поэтому 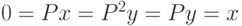 . Следовательно,
. Следовательно,  . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.(Верный ответ)
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.(Верный ответ)
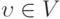 можно представить в виде
можно представить в виде 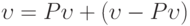 , где
, где  и
и 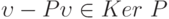 . Кроме того, если
. Кроме того, если 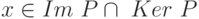 , то
, то  . В самом деле, тогда
. В самом деле, тогда 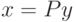 и
и  , поэтому
, поэтому 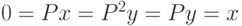 . Следовательно,
. Следовательно,  . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.(Верный ответ)
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.(Верный ответ)

 в базисе
в базисе 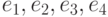 имеет матрицу
имеет матрицу 
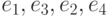 ?
? имеет матрицу
имеет матрицу 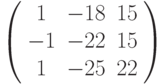
 ?
?
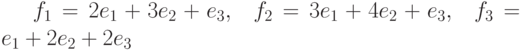 ?
?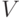 в базисе
в базисе 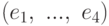 имеет матрицу
имеет матрицу 
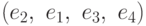 ?
?![R\left[ x\right] _{2}](https://intuit.ru//sites/default/files/tex_cache/a081aa90a0b0b090ea47e74c0f77e837.png) имеет в базисе
имеет в базисе 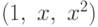 матрицу
матрицу 
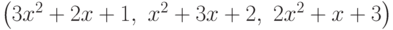 ?
?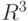 имеет в базисе
имеет в базисе 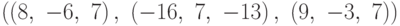 матрицу
матрицу 
 ?
?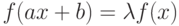 следует, что
следует, что 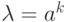 , где k - степень
, где k - степень  . Приведенное выше доказательство, доказывает, что:
. Приведенное выше доказательство, доказывает, что: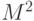 задано скалярное произведение
задано скалярное произведение  . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
. Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора 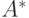 в базисе
в базисе  ?
?