Пусть функция  - решение дифференциального уравнения
- решение дифференциального уравнения 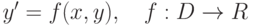 . Тогда
. Тогда
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
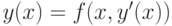
область определения 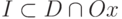 (Верный ответ)
(Верный ответ)
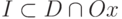 (Верный ответ)
(Верный ответ)
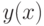 - дифференцируемая на
- дифференцируемая на 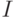 функция(Верный ответ)
функция(Верный ответ)
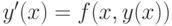 (Верный ответ)
(Верный ответ)

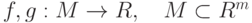 .
.  и
и 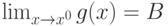 . Тогда функция
. Тогда функция  имеет предел и он равен
имеет предел и он равен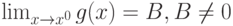 . Тогда функция
. Тогда функция 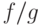 имеет предел и он равен
имеет предел и он равен имеет предел и он равен
имеет предел и он равен и
и 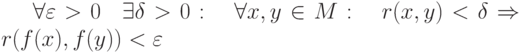 . Тогда функция
. Тогда функция  называется
называется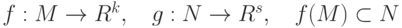 . Сложная функция
. Сложная функция 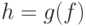 непрерывна
непрерывна 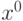 , если
, если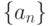 и
и 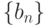 сходятся и
сходятся и  . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен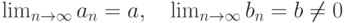 . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен - множество сходимости последовательности
- множество сходимости последовательности  . Функция
. Функция  является пределом последовательности
является пределом последовательности  .Тогда последовательность
.Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен