Пусть выборка 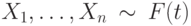 , а выборка
, а выборка 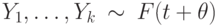 . Для проверки гипотезы
. Для проверки гипотезы 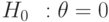 применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение
применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение 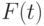 - непрерывное распределение с нулевой медианой. Чему равна нижняя граница
- непрерывное распределение с нулевой медианой. Чему равна нижняя граница 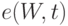 АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
(Отметьте один правильный вариант ответа.)
Варианты ответа
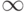
0
0.86(Верный ответ)
0.5
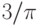

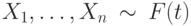 , а выборка
, а выборка 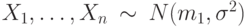 и
и 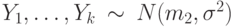 . Проверяется гипотеза
. Проверяется гипотеза  . Для проверки этой гипотезы применяют критерий Вилкоксона и критерий Стьюдента. Чему равна АОЭ (асимптотическая относительная эффективность) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
. Для проверки этой гипотезы применяют критерий Вилкоксона и критерий Стьюдента. Чему равна АОЭ (асимптотическая относительная эффективность) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?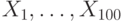 из распределения
из распределения 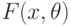 требуется проверить гипотезу о том, что неизвестный параметр
требуется проверить гипотезу о том, что неизвестный параметр 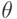 равен 5 против альтернативы о том, что значение параметра
равен 5 против альтернативы о том, что значение параметра 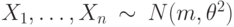 с известным математическим ожиданием
с известным математическим ожиданием  построены доверительные интервалы уровня надежности
построены доверительные интервалы уровня надежности 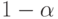 для параметра
для параметра 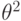 .Обозначим
.Обозначим 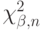 - квантиль уровня
- квантиль уровня  распределения хи-квадрат с
распределения хи-квадрат с  степенями свободы. Какой из представленных интервалов является центральным доверительным интервалом параметра
степенями свободы. Какой из представленных интервалов является центральным доверительным интервалом параметра  построены доверительные интервалы уровня надежности
построены доверительные интервалы уровня надежности 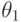 .Обозначим
.Обозначим  - выборочную дисперсию, а
- выборочную дисперсию, а  -квантиль уровня
-квантиль уровня  имеет равномерное распределение
имеет равномерное распределение 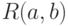 , а выборка
, а выборка  имеет равномерное распределение
имеет равномерное распределение 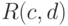 . В каком случае эти выборки будут являться однородными?
. В каком случае эти выборки будут являться однородными?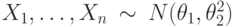 , а выборка
, а выборка 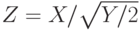 , где случайная величина
, где случайная величина  имеет стандартное нормальное распределение
имеет стандартное нормальное распределение  , а случайная величина
, а случайная величина  имеет распределение хи-квадрат с двумя степенями свободы (
имеет распределение хи-квадрат с двумя степенями свободы ( ). Известно, что
). Известно, что  ?
?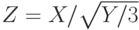 , где случайная величина
, где случайная величина  ). Известно, что
). Известно, что