Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования - ответы
Количество вопросов - 179
Дано нечеткое множество 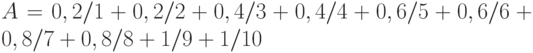 Множеством
Множеством  уровня является множество:
уровня является множество:
Промежуточная продукция в межотраслевом балансе это -
Частотное распределение выходного показателя имитационной модели в Mathcad строится с использованием функции:
Спрос на товары второй необходимости выражается функцией Торнквиста 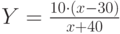 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
В качестве управляемых переменных в оптимизационных моделях в экономике используются:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, в результате исследования за ожидаемое значение чистой приведенной стоимости прибыли следует принять:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Выходной исследуемый показатель:
Если в оптимизационной задаче поиска максимума целевой функции все условия ограничивают переменные снизу, то результат будет:
Какой аргумент финансовых функций учитывает разное поступление платежей в течение периода финансовой ренты:
Выражение ![r\cdot [\frac{f\nu}{[(1+r)^n-1]}](https://intuit.ru//sites/default/files/tex_cache/0841dc2691944448e22c257ebbe1a0db.png) лежит в основе расчета
лежит в основе расчета
Функция принадлежности нечеткого множества  , определенного на множестве
, определенного на множестве 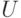 , это:
, это:
Функция 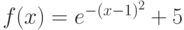 имеет перегибы при значениях x, равных:
имеет перегибы при значениях x, равных:
В транспортной задаче с промежуточными пунктами тариф транспортировки от первичного поставщика к конечному потребителю принимается равным:
Чистая современная (приведенная) стоимость определяется как :
Какой смысл имеют элементы матрицы  .
.
Конечный продукт  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ 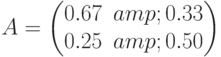 . Матрица межотраслевых поставок имеет вид:
. Матрица межотраслевых поставок имеет вид:
Для функции, заданной в виде  , значение
, значение  равно:
равно:
Коэффициент прямых затрат производства продукции это:
Валовый продукт  , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 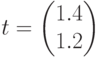 . Общие затраты труда составят:
. Общие затраты труда составят:
Оптимизационная задача в Mathcad может быть решена с помощью:
Имитационная выборка выходного показателя создается в результате:
Рассматривается задача оптимальной производственной программы с заданным планом при нехватке имеющихся ресурсов. При построении оптимизационной модели в "комплектной постановке" задача имеет решение:
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый, и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. При оптимизации полного фонда оплаты (минимальный) минимальный фонд (оплата всех сотрудников) составит:
Если E – единичная матрица, A-матрица прямых затрат, матрица, B - матрица полных затрат имеет вид:
Дано нечеткое множество 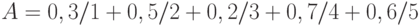 . Индекс нечеткости
. Индекс нечеткости 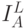 по линейной метрике равен:
по линейной метрике равен:
Для компьютерной имитации параметров имитационной модели в Mathcad используются функции из категории:
Характеристическая функция "обычного" множества 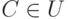 это -
это -
Что такое стохастические переменные?
В методе Монте-Карло учитывается влияние на исследуемую систему:
Для анализа результатов имитационного моделирования методом Монте - Карло для выходного показателя рассчитываются:
Функция 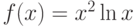 имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
Экстремальное значение функции  для x>0 равно:
для x>0 равно:
Функция rows(А) определяет:
Для системы уравнений 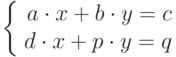 корень решения x равен:
корень решения x равен:
Производная 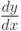 для функций, заданных параметрически:
для функций, заданных параметрически: 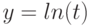 равна:
равна:
Пусть производительность труда от времени t характеризуется функцией 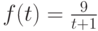 , объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
, объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
Функция спроса имеет вид 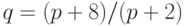 , функция предложения
, функция предложения 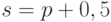 , где
, где 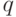 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
Спрос на товары первой необходимости выражается функцией Торнквиста 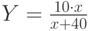 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
Сумма 2000 ед. вырастет до 8000 ед. при вложении в банк под ставку 10% (с учетом капитализации) за срок:
Если сложные проценты начисляются несколько раз в году, то при финансовых расчетах годовая процентная ставка:
Выражение 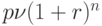 лежит в основе расчета
лежит в основе расчета
Выражение для современной стоимости постоянной финансовой ренты имеет вид:
Финансовая рента пренумерандо - рента, для которой:
Ссуда в 4000 ед. получена под ставку 10% в год. Через два года возвращаемая сумма составит:
При расчете наращенной суммы за n периодов по схеме сложных процентов
Сумма 1000 ед. вырастет до 5000 ед. при вложении в банк под ставку 8% годовых с ежемесячным начислением процентов за срок:
Выражение  лежит в основе расчета
лежит в основе расчета
Сумма 5000 руб., за 2,5 года выросла до 7000 руб. при начислении сложных процентов, доходность операции составила:
Сумма в 20000 ед. , помещена в банк. под ставку 8% годовых с последующим ежегодным пополнением суммами в 5000. ед.. Проценты начисляются раз в год с капитализацией. Сумма к концу 3 года составит:
Валовая продукция в межотраслевом балансе:
Структура добавленной стоимости МОБ состоит из компонентов:
Какой смысл имеют элементы матрицы полных затрат bij:
Коэффициент прямых затрат труда это:
Какой показатель является устойчивым в плановом периоде относительно отчётного периода:
Конечный продукт 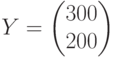 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 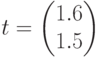 . Общие затраты труда составят:
. Общие затраты труда составят:
Продуктивность матрицы коэффициентов прямых затрат означает:
Конечный продукт  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ 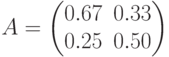 . Вектор валового продукта равен:
. Вектор валового продукта равен:
Валовый продукт 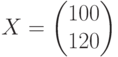 , матрица межотраслевых поставок
, матрица межотраслевых поставок 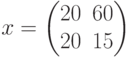 . Конечный продукт равен:
. Конечный продукт равен:
Валовый продукт  , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ  , затраты живого труда
, затраты живого труда 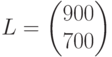 , вектор полной трудоемкости Т равен:
, вектор полной трудоемкости Т равен:
Количество аргументов целевой функции в оптимизационной задаче равно:
Факторы, порождающие ограничения в оптимизационных моделях экономических задач:
Если в оптимизационной задаче поиска минимума целевой функции все условия ограничивают переменные сверху, то результат будет:
Пусть на трех складах хранится однотипная продукция  , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 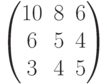 . Оптимальные минимальные затраты транспортировки составляют:
. Оптимальные минимальные затраты транспортировки составляют:
В транспортной задаче, когда общее количество груза меньше, чем требуется потребителям, вводится:
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны  . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 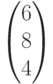 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Максимальная оптимальная прибыль (усл. ед.) составит:
. Максимальная оптимальная прибыль (усл. ед.) составит:
Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При построении оптимизационной модели с добавлением ресурсов задача имеет решение:
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны  . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 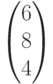 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
Что такое имитационная модель экономического процесса?
Моделирование последовательностей случайных величин использует
Результаты имитационного эксперимента могут быть использованы
Результаты имитационного моделирования могут быть использованы для:
Для проведения имитационного эксперимента необходимо провести компьютерную имитацию:
При анализе результатов имитационного эксперимента мерой рисковых значений для выходного показателя является:
Процентный разброс исследуемого показателя около среднего значения определяет:
Для анализа результатов имитационного эксперимента необходимо:
Дайте определения нечеткого множества А:
Нечеткое множество 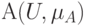 называют нормальным,
называют нормальным,
Выберите носитель для нечеткого множества 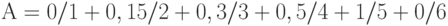
Выберите точку перехода для нечеткого множества 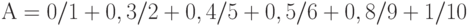 .
.
Как называется функция принадлежности, описываемая законом
Обычным множеством, ближайшим к нечеткому множеству  , называется: подмножество
, называется: подмножество 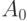 множества U, характеристическая функция которого имеет вид:
множества U, характеристическая функция которого имеет вид:
Термин супремум обозначает :
Какие инструменты MathCad можно использовать для построения множества a–уровня для нечеткого множества А (U,mA)
В задаче оптимальной производственной программы структура выпуска – это:
Валовый продукт 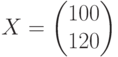 , матрица межотраслевых поставок
, матрица межотраслевых поставок 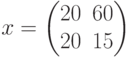 . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны  . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 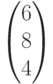 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
Коэффициент полных затрат труда это:
Выбрать нечеткое множество, для которого супремум=0,8
Выберите нечеткое множество, для которого точка перехода это элемент {1}
Будущая стоимость платежа при увеличении количества начислений сложных процентов в течение года:
Функция спроса имеет вид  , функция предложения
, функция предложения 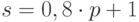 , где
, где 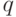 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
Метод Монте-Карло использует законы
Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи в "комплектной постановке" (использование только имеющихся ресурсов) в качестве управляемых переменных выбираются:
Имеется нечеткое множество  . Выбрать множество значений функции принадлежности
. Выбрать множество значений функции принадлежности  для него:
для него:
Производная 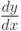 для функций, заданных параметрически:
для функций, заданных параметрически: 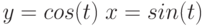 , равна:
, равна:
Как называется функция принадлежности, описываемая законом
Для функции, заданной в виде 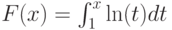 , значение
, значение 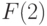 равно:
равно:
Экстремальное значение функции 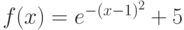 равно:
равно:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Детерминированные переменные задачи:
Функции стохастических аргументов являются
Ссуда в 5000 ед. получена на полтора года под ставку 10% годовых с ежеквартальным начислением. Возвращаемая сумма составит:
Нечеткое множество 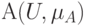 называют субнормальным, -
называют субнормальным, -
Множество  –уровня для нечеткого множества
–уровня для нечеткого множества  составляется для:
составляется для:
В результате моделирования Монте-Карло разные прогнозные сценарии создаются за счет:
Функция  при x>0 имеет экстремум при значении x, равном:
при x>0 имеет экстремум при значении x, равном:
Функция 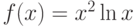 имеет перегиб при значении x, равном:
имеет перегиб при значении x, равном:
Для системы уравнений 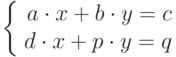 корень решения y равен:
корень решения y равен:
Для функции, заданной в виде 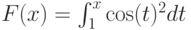 , значение
, значение  равно:
равно:
Пусть производительность труда от времени t характеризуется функцией 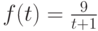 , объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
Функция спроса имеет вид 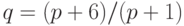 , функция предложения
, функция предложения  , где
, где 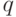 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
Спрос на товары второй необходимости, который выражается функцией Торнквиста 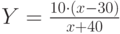 , где
, где  - доход, появляется, если доход достигнет величины :
- доход, появляется, если доход достигнет величины :
Если сложные проценты начисляются несколько раз в году, то при финансовых расчетах срок финансовой операции:
Выражение ![(f\nu/p\nu)^{1/n}-1]](https://intuit.ru//sites/default/files/tex_cache/cde74de8ce78c61452c9e96657d61d9d.png) лежит в основе расчета:
лежит в основе расчета:
Выражение для наращенной стоимости постоянной финансовой ренты имеет вид:
На депозит отчисляются суммы в размере 3000 каждый квартал под ставку 10% годовых. Проценты начисляются ежеквартально с капитализацией. Сумма к концу 2 года составит:
Уравнение межотраслевого баланса имеет вид:
Какой смысл имеют элементы матрицы прямых затрат aij:
Коэффициент полных затрат продукции – это:
Конечный продукт  , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ 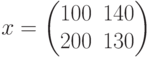 , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 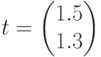 . Общие затраты труда составят:
. Общие затраты труда составят:
Конечный продукт  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ 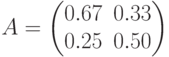 . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
В качестве целевой функции в экономической оптимизационной задаче выбирается
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны  . Нормы прибыли (в усл.ед) от реализации каждого вида равны
. Нормы прибыли (в усл.ед) от реализации каждого вида равны 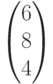 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  , для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
, для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. При оптимизации полного фонда оплаты (минимальный) оплата инженеров составит:
При имитационном моделировании необходимо задать:
При использовании Монте-Карло неопределенные данные задаются как:
Для компьютерной имитации параметра имитационной модели в Mathcad используется функция:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Стохастические переменные задачи:
Выберите нечеткое множеств, которое является нормальным:
Для какого нечеткого множества приведенное множество  является ближайшим к нечеткому.
является ближайшим к нечеткому.
Выбрать супремум для нечеткого множества: 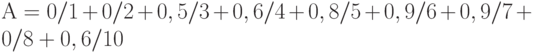
Какие инструменты MathCad можно использовать для представления нечеткого множества:
Даны два нечетких множества 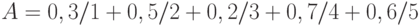 и
и 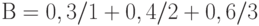 Сравнить индексы нечеткости по линейной метрике:
Сравнить индексы нечеткости по линейной метрике:
Валовый продукт  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда 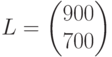 , вектор полной трудоемкости T равен:
, вектор полной трудоемкости T равен:
Пусть на трех складах хранится однотипная продукция  , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 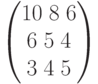 . Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
. Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
Какие инструменты MathCad можно использовать для построения функции принадлежности нечеткого множества .
При анализе результатов имитационного эксперимента за ожидаемое значение выходного показателя следует принять:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, для измерения риска проекта следует определить:
Множеством  –уровня нечеткого множества
–уровня нечеткого множества  называется :
называется :
Точкой перехода нечеткого множества называют:
Функция 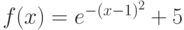 имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
Несущим множеством или носителем нечеткого множества A, определенного на множестве U, называют:
Дисконтирование позволяет:
Выражение ![r\cdot [\frac{f\nu}{[(1+r)^n-1]\cdot(1+r)}](https://intuit.ru//sites/default/files/tex_cache/7352364bf4344d61060c2c32029fb1b9.png) лежит в основе расчета
лежит в основе расчета
Функция  имеет перегиб (для x>0 ) при значении x, равном:
имеет перегиб (для x>0 ) при значении x, равном:
Пусть производительность труда от времени t характеризуется функцией 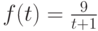 , объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
Современная стоимость суммы 7000 ед, полученной через 4,5 года после вложения инвестиции, при уровне доходности 12% составит:
Конечная продукция в межотраслевом балансе -
Структура конечного продукта МОБ состоит из компонентов :
Конечный продукт  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда 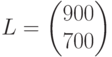 , вектор полной трудоемкости T равен:
, вектор полной трудоемкости T равен:
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый, и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. Каких сотрудников надо привлечь для выполнения всего проекта, чтобы фонд оплаты был минимальным:
Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи с добавлением ресурсов - в качестве управляемых переменных выбираются:
Цель имитационного моделирования методом Монте-Карло -
Для оценки риска выходному показателю принять значение больше (меньше) заданного используется функция:
Выбрать для нечеткого множества 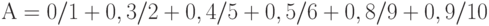 множество, ближайшее к нечеткому.
множество, ближайшее к нечеткому.
Имеется нечеткое множество  и обычное множество
и обычное множество 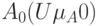 ближайшее к нечеткому множеству
ближайшее к нечеткому множеству  , индекс нечеткости по линейной метрике
, индекс нечеткости по линейной метрике 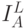 множества
множества  определяется по формуле:
определяется по формуле:
Какие методы используются при решении задачи оптимизации?
Пусть на трех складах хранится однотипная продукция  , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 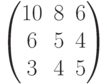 . Для выполнения заказа и обеспечения минимальных затрат необходимо:
. Для выполнения заказа и обеспечения минимальных затрат необходимо:
Результат имитационного эксперимента зависит:
Выражение для наращенной стоимости элементарного потока имеет вид:
Действие функции stack (M1,M2) над матрицами M1 и M2 :
Производная 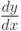 для функций, заданных параметрически:
для функций, заданных параметрически: 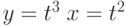 равна:
равна:
Если t и T – векторы прямой и полной трудоемкости, X и Y – векторы - валовой и конечной продукции, то уравнение межотраслевого баланса труда имеет вид.
Выражение 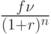 лежит в основе расчета:
лежит в основе расчета:
Определите основные типы функций принадлежности:
Валовый продукт 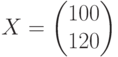 , матрица межотраслевых поставок
, матрица межотраслевых поставок 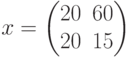 . матрица прямых затрат равна:
. матрица прямых затрат равна:
Множество имеет вид 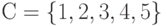 . Для какого нечеткого множества оно является несущим :
. Для какого нечеткого множества оно является несущим :
Функция  определяет:
определяет:
Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи в "комплектной постановке" (использование только имеющихся ресурсов) в качестве целевой функции выбирается:
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны  . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 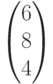 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
Банк принимает вклады под 8% годовых, проценты начисляются ежемесячно с учетом капитализации, эффективная годовая процентная ставка составит:
Коэффициенты прямых затрат должны удовлетворять следующим условиям:
Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи с добавлением ресурсов - в качестве целевой функции выбирается:
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, для оценки эффективности проекта следует определить:
Финансовая рента постнумерандо - рента, для которой:
Для системы уравнений 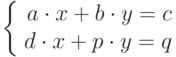 соотношение между a,b.d,p, при котором система не имеет решений, имеет вид:
соотношение между a,b.d,p, при котором система не имеет решений, имеет вид:
В транспортной задаче, когда общее количество груза больше, чем требуется потребителям, вводится
Сумма 5000 ед. вырастет до 10000 ед. при вложении в банк под ставку 10% годовых с ежеквартальным начислением процентов за срок:
Экстремальное значение функции 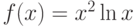 равно:
равно:
В банк отчисляются суммы в размере 2000 в начале каждого месяца под ставку 8% годовых. Проценты начисляются ежемесячно с капитализацией. Сумма к концу года составит:

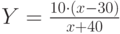 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит: , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 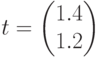 . Общие затраты труда составят:
. Общие затраты труда составят: 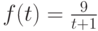 , объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
, объем произведенной работы (в усл. ед.) за первый час рабочего дня равен: 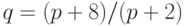 , функция предложения
, функция предложения 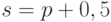 , где
, где 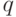 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна: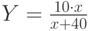 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит: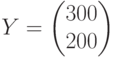 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 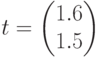 . Общие затраты труда составят:
. Общие затраты труда составят:  , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ  , затраты живого труда
, затраты живого труда 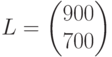 , вектор полной трудоемкости Т равен:
, вектор полной трудоемкости Т равен:  , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 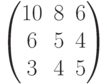 . Оптимальные минимальные затраты транспортировки составляют:
. Оптимальные минимальные затраты транспортировки составляют: . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 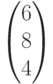 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Максимальная оптимальная прибыль (усл. ед.) составит:
. Максимальная оптимальная прибыль (усл. ед.) составит:  . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 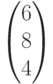 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит: , называется: подмножество
, называется: подмножество 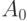 множества U, характеристическая функция которого имеет вид:
множества U, характеристическая функция которого имеет вид: . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 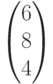 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит : , функция предложения
, функция предложения 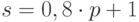 , где
, где 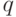 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна: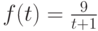 , объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за второй час рабочего дня составит: 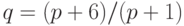 , функция предложения
, функция предложения  , где
, где 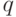 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна: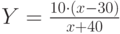 , где
, где  - доход, появляется, если доход достигнет величины :
- доход, появляется, если доход достигнет величины :  , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ 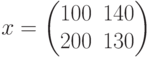 , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции 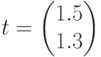 . Общие затраты труда составят:
. Общие затраты труда составят:  . Нормы прибыли (в усл.ед) от реализации каждого вида равны
. Нормы прибыли (в усл.ед) от реализации каждого вида равны 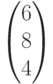 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  , для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
, для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции: , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда 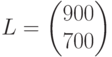 , вектор полной трудоемкости T равен:
, вектор полной трудоемкости T равен:  , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 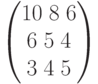 . Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
. Для обеспечения минимальных затрат 1 потребителю необходимо получить груз: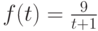 , объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:  , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда 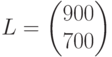 , вектор полной трудоемкости T равен:
, вектор полной трудоемкости T равен:  и обычное множество
и обычное множество 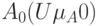 ближайшее к нечеткому множеству
ближайшее к нечеткому множеству  , индекс нечеткости по линейной метрике
, индекс нечеткости по линейной метрике 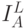 множества
множества  определяется по формуле:
определяется по формуле: , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей 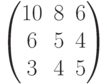 . Для выполнения заказа и обеспечения минимальных затрат необходимо:
. Для выполнения заказа и обеспечения минимальных затрат необходимо: . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны 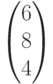 . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит: