Введение в Octave - ответы
Количество вопросов - 286
Найдите произведение элементов вектора кумулятивной суммы элементов вектора ![[2:3:10]](https://intuit.ru//sites/default/files/tex_cache/077370dd41e5cd9d62b3e93211cb893c.png) . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите сумму элементов массива ![([1,3,4,5].*[2,4,6,8])(:)(2)](https://intuit.ru//sites/default/files/tex_cache/4f2641dc01fd8f1f159a73428bfd355f.png) . Ответ округлите до целых.
. Ответ округлите до целых.
Исследуйте функцию 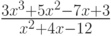 . На каком отрезке функция монотонно возрастает?
. На каком отрезке функция монотонно возрастает?
Выберите функцию, объединяющую матрицы-аргументы.
Выберите верное утверждение:
Выберите верные утверждения:
С помощью какого символа разделяются строки матриц при их записи в виде массива?
С помощью какой команды можно удалить ранее объявленную переменную?
Дано выражение  . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат.
Дано 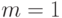 . Какие из приведенных ниже команд вернут значение
. Какие из приведенных ниже команд вернут значение  ?
?
Какая из приведенных ниже точек (x,y) лежит внутри части плоскости, ограниченной линиями  ,
, 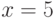 ,
,  ,
, 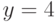 ?
?
Укажите значение параметра функции  , позволяющее добавлять в конец непустого текстового файла информацию и считывать её.
, позволяющее добавлять в конец непустого текстового файла информацию и считывать её.
Какая функция позволяет считывать данные из открытого файла?
Выберите функцию, позволяющую построить анимационный ролик.
Выберите функцию, создающую пустое графическое окно.
Выберите функцию, позволяющую удалить объект в графическом окне.
Выберите функцию, предназначенную для вывода заголовка графика.
Найдите сумму элементов массива ![([1,3,4,5]./[2,4,6,8])(:)(2)](https://intuit.ru//sites/default/files/tex_cache/0d1e8579c4d5abb06144d67c19280390.png) . Ответ округлите до целых.
. Ответ округлите до целых.
Выберите функцию, вычисляющую векторное произведение векторов.
Даны координаты точек  ,
,  и
и  ,
, 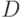 . Выберите четверки точек такие, что векторы
. Выберите четверки точек такие, что векторы  и
и 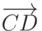 коллинеарны.
коллинеарны.
Даны координаты точек: 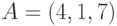 и
и  . Выберите параметрическое уравнение прямой, проходящей через эти точки.
. Выберите параметрическое уравнение прямой, проходящей через эти точки.
Выберите функцию, позволяющую вычислить произведение многочленов.
Даны два многочлена  и
и 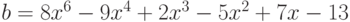 . Какой вид будет иметь остаток от деления
. Какой вид будет иметь остаток от деления  на
на  ?
?
Выберите функцию, позволяющую решить систему нелинейных уравнений.
Выберите функцию, позволяющую вычислить производную функции в технике символьных вычислений.
Выберите встроенную функцию, позволяющую решить оптимизационную задачу.
Какие операции совершаются при вызове функции  , где
, где  -- файл, в который производилась запись информации?
-- файл, в который производилась запись информации?
Выберите функцию, возвращающую указатель на текущий графический объект.
Какая из приведенных ниже точек (x,y) лежит внутри части плоскости, ограниченной линиями  ,
, 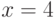 ,
,  ,
, 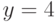 ?
?
Какая команда вернет значение числа  ?
?
Выберите функцию, создающую оси с определенными свойствами.
Даны векторы: 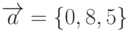 ,
, 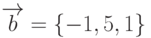 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов 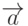 и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.
Организуйте решение модифицированным методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Вычислите значение интеграла от полинома 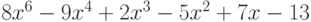 в точке
в точке  (постоянная интегрирования нулевая). Ответ округлите до целого.
(постоянная интегрирования нулевая). Ответ округлите до целого.
Вычислите значение выражения 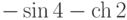 . Результат округлите до ближайшего целого в сторону отрицательной бесконечности. Ответ -- целое число.
. Результат округлите до ближайшего целого в сторону отрицательной бесконечности. Ответ -- целое число.
Вычислите интеграл  по квадратуре Гаусса. Точность -- по умолчанию. В ответ записать количество итераций, за которое был вычислен интеграл (целое число).
по квадратуре Гаусса. Точность -- по умолчанию. В ответ записать количество итераций, за которое был вычислен интеграл (целое число).
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 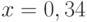 для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Даны матрицы ![A=[3,1,0; 2,5,6; 0,1,1]](https://intuit.ru//sites/default/files/tex_cache/6615ab7a5beae0d0bab93d8b20d4d951.png) и
и ![B=[1,2,3; 0,1,1; 2,3,4]](https://intuit.ru//sites/default/files/tex_cache/382ad8c75ee46619b7d7bca351c2a660.png) . Решите матричное уравнение
. Решите матричное уравнение 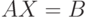 . В ответ запишите значение определителя полученной матрицы
. В ответ запишите значение определителя полученной матрицы  , округлив результат до одного знака после запятой.
, округлив результат до одного знака после запятой.
Решите уравнение 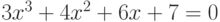 . Сложите значения всех корней. В ответ запишите действительную часть результата с точностью до 2-х знаков после запятой.
. Сложите значения всех корней. В ответ запишите действительную часть результата с точностью до 2-х знаков после запятой.
Организуйте решение методом Милна дифференциального уравнения: 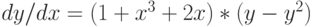 . Начальные условия
. Начальные условия 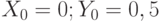 . Шаг 0,01. В ответ укажите значение
. Шаг 0,01. В ответ укажите значение 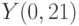 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 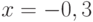 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 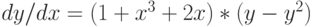 . Начальные условия
. Начальные условия 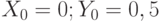 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 8-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 8-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Постройте график функции  . Найдите количество локальных максимумов функции на отрезке
. Найдите количество локальных максимумов функции на отрезке ![\[ 0, 3\]](https://intuit.ru//sites/default/files/tex_cache/e749596926d59dbb4d3e9b8ba01b5ac6.png) . Ответ -- целое число.
. Ответ -- целое число.
Найдите минимум функции 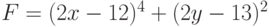 при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите угол (в радианах) между плоскостями, заданными уравнениями 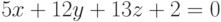 ,
,  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.
Подберите коэффициенты полинома 4-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 4-ой степени
. В ответе укажите коэффициент при 4-ой степени  . Ответ округлите до 3-го знака после запятой.
. Ответ округлите до 3-го знака после запятой.
Дана матрица ![M=[1,2,3,4,5;5,4,3,2,1;6,7,8,9,0;0,9,8,7,6;9,7,5,4,3]](https://intuit.ru//sites/default/files/tex_cache/c3da0038a7e9419ffbc1015439c5ba31.png) . Найдите сумму элементов массива
. Найдите сумму элементов массива 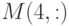 . Ответ -- целое число.
. Ответ -- целое число.
Даны векторы, заданные координатами начала и конца: 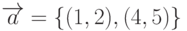 ,
, 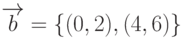 и
и 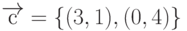 . Найдите длину вектора
. Найдите длину вектора 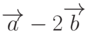 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Решите уравнение  . Найдите сумму действительных частей корней этого уравнения. Ответ округлить до целых в меньшую сторону.
. Найдите сумму действительных частей корней этого уравнения. Ответ округлить до целых в меньшую сторону.
Организуйте решение методом Кутта-Мерсона дифференциального уравнения: 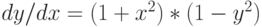 . Начальные условия
. Начальные условия 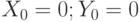 . Шаг 0,1, точность 0,1. В ответ укажите значение
. Шаг 0,1, точность 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (ответ округлите до трех знаков после запятой).
Постройте графики функций  и
и 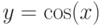 . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число.
Найдите минимум функции 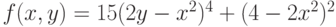 . В ответ запишите значение
. В ответ запишите значение  , при котором достигается минимум. Ответ округлите до 2-го знака после запятой.
, при котором достигается минимум. Ответ округлите до 2-го знака после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 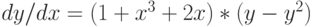 . Начальные условия
. Начальные условия 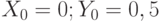 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Подберите коэффициенты полинома 6-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.
Даны векторы: 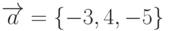 ,
, 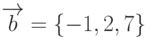 . Найдите угол между векторами
. Найдите угол между векторами 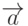 и
и  в радианах. Ответ округлить до 1-го знака после запятой.
в радианах. Ответ округлить до 1-го знака после запятой.
Уравнение прямой в параметрической форме имеет вид 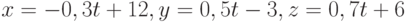 . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью 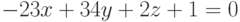 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Вычислите определитель матрицы (ответ -- целое число):
| 1 | 2 | 5 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 4 | 4 | 0 |
Дана матрица. Найдите сумму элементов обратной к ней матрицы. Ответ -- целое число.
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
Вычислите значение выражения 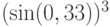 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой.
Вычислите значение выражения 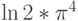 . В ответе запишите действительную часть числа, округленную до четырех знаков после запятой (использовать обычное округление).
. В ответе запишите действительную часть числа, округленную до четырех знаков после запятой (использовать обычное округление).
Вычислите cколько раз число 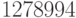 нацело делится на число
нацело делится на число  . Результат сложите с остатком от деления этих чисел. Ответ -- целое число.
. Результат сложите с остатком от деления этих чисел. Ответ -- целое число.
Вычислите значение выражения  . Модуль результата округлите до четырех знаков после запятой.
. Модуль результата округлите до четырех знаков после запятой.
Вычислите значение выражения  . Мнимую часть результата округлите до четырех знаков после запятой.
. Мнимую часть результата округлите до четырех знаков после запятой.
Задан массив 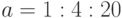 . В ответ запишите сумму всех его элементов (целое число).
. В ответ запишите сумму всех его элементов (целое число).
Реализуйте функцию  Вычислите
Вычислите  . Ответ -- целое число.
. Ответ -- целое число.
Определить количество простых делителей числа 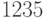 , не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
, не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
Дан массив 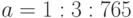 . Найти сумму его нечетных элементов. Ответ -- целое число.
. Найти сумму его нечетных элементов. Ответ -- целое число.
Реализуйте функцию, вычисляющую числа Фибоначчи (первые два числа -- единицы, каждое последующее равно сумме двух предыдущих). Вычислите 16-е число Фибоначчи. Ответ -- целое число.
Постройте график функции  . Найдите количество локальных минимумов функции на отрезке
. Найдите количество локальных минимумов функции на отрезке ![\[ 3, 6\]](https://intuit.ru//sites/default/files/tex_cache/e85becbdfa3b398fb43c646ea2fe0498.png) . Ответ -- целое число.
. Ответ -- целое число.
Постройте в полярной системе координат графики функций  и
и 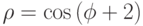 при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Постройте функции 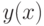 , заданные параметрически:
, заданные параметрически: 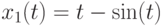 ,
,  и
и 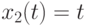 ,
,  при
при ![t\in \[0, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/fd1fe5dda34ed5256fcc066c0350c1dc.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Дан вектор ![a=[5,4,3,2,1,0]](https://intuit.ru//sites/default/files/tex_cache/a682f10c56ac154a3064a2d68aae4e9d.png) . Укажите значение
. Укажите значение  . Ответ -- целое число.
. Ответ -- целое число.
Дана матрица ![M=[1,2,3,4,5;5,4,3,2,1;6,7,8,9,0;0,9,8,7,6;9,7,5,4,3]](https://intuit.ru//sites/default/files/tex_cache/c3da0038a7e9419ffbc1015439c5ba31.png) . Преобразуйте матрицу следующим образом:
. Преобразуйте матрицу следующим образом: ![M(1:3, 3:4)=[1,1;2,2;4,5]](https://intuit.ru//sites/default/files/tex_cache/7e4b9b9b9b20508535e48a1755d058fb.png) . Найдите сумму элементов массива
. Найдите сумму элементов массива 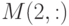 . Ответ -- целое число.
. Ответ -- целое число.
Даны матрицы ![M_{1}=[1,2,3;5,4,3;6,7,8]](https://intuit.ru//sites/default/files/tex_cache/57c3b4be070ea328d34473f411b584fc.png) и
и ![M_{2}=[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/960bc0723691bc60e235ec9800f0f72a.png) . Найдите сумму элементов 1-ой строки матрицы
. Найдите сумму элементов 1-ой строки матрицы 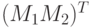 , (
, ( -- означает транспонирование). Ответ -- целое число.
-- означает транспонирование). Ответ -- целое число.
Найдите сумму собственных значений матрицы ![[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/385363aa456979c4891664829cfd5d99.png) . Ответ округлите до целого.
. Ответ округлите до целого.
Решить систему линейных алгебраических уравнений, заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
| 1 | 2 | 3 | 2 | 1 | | 39 |
| 3 | 6 | 4 | 1 | 2 | | 61 |
| 2 | 3 | 2 | 6 | 2 | | 76 |
| 3 | 6 | 3 | 3 | 3 | | 75 |
| 1 | 2 | 3 | 4 | 2 | | 56 |
Даны векторы, заданные координатами начала и конца: 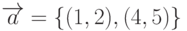 ,
, 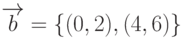 и
и 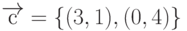 . Найдите длину вектора
. Найдите длину вектора  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Даны векторы:  ,
, 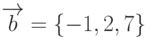 . Найдите угол между векторами
. Найдите угол между векторами 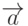 и
и  в радианах. Ответ округлить до 1-го знака после запятой.
в радианах. Ответ округлить до 1-го знака после запятой.
Найдите угол (в радианах) между плоскостями, заданными уравнениями 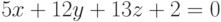 ,
, 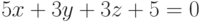 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Даны векторы:  ,
, 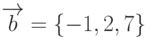 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов 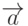 и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.
Найдите угол (в радианах) между плоскостями, заданными уравнениями 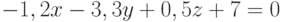 ,
,  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Уравнение прямой в параметрической форме имеет вид 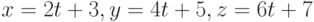 . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Вычислите производную от полинома  . В ответе приведите сумму коэффициентов при степенях
. В ответе приведите сумму коэффициентов при степенях  получившегося полинома. Ответ -- целое число.
получившегося полинома. Ответ -- целое число.
Вычислите значение интеграла от полинома 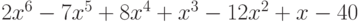 в точке
в точке  (постоянная интегрирования равна
(постоянная интегрирования равна  ). Ответ округлите до целого.
). Ответ округлите до целого.
Найдите сумму корней уравнения 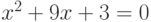 . Ответ округлить до целых в меньшую сторону.
. Ответ округлить до целых в меньшую сторону.
Решите уравнение  . Найдите сумму действительных частей корней этого уравнения. Ответ округлить до 2-го знака после запятой (в меньшую сторону).
. Найдите сумму действительных частей корней этого уравнения. Ответ округлить до 2-го знака после запятой (в меньшую сторону).
Решите систему уравнений: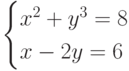 В ответ введите значение действительного корня
В ответ введите значение действительного корня  с точностью до 2-го знака после запятой.
с точностью до 2-го знака после запятой.
Вычислите вторую производную функции 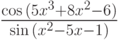 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 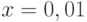 . Ответ округлите до 1-го знака после запятой (в меньшую сторону).
. Ответ округлите до 1-го знака после запятой (в меньшую сторону).
Вычислите по формуле Ньютона-Лейбница определенный интеграл  (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
Вычислите интеграл 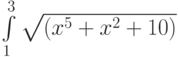 методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Вычислите интеграл  методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Вычислите интеграл  методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
Организуйте решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение 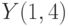 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Организуйте решение модифицированным методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение 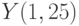 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Адамса дифференциального уравнения: 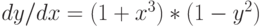 . Начальные условия
. Начальные условия 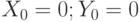 . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Милна дифференциального уравнения: 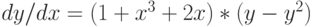 . Начальные условия
. Начальные условия 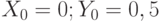 . Шаг 0,1. В ответ укажите значение
. Шаг 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 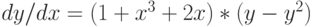 . Начальные условия
. Начальные условия 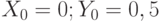 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 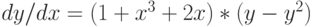 . Начальные условия
. Начальные условия 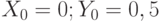 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Найдите минимум функции 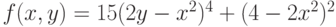 . Ответ округлите до целого.
. Ответ округлите до целого.
Найдите минимум функции  при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите минимум функции  при ограничениях:
при ограничениях:  Ответ округлите целых.
Ответ округлите целых.
Найдите минимум функции 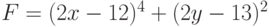 при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите такие значения переменных  ,
,  , при которых целевая функция
, при которых целевая функция 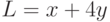 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 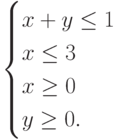 В ответ запишите максимальное значение
В ответ запишите максимальное значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 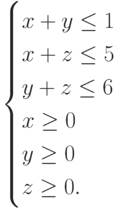 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 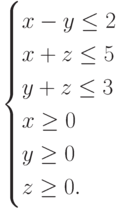 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Подберите коэффициенты полинома 4-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до 3-го знака после запятой.
. Ответ округлите до 3-го знака после запятой.
Подберите коэффициенты полинома 5-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 4-ой степени
. В ответе укажите коэффициент при 4-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.
Вычислите среднее арифметическое массива значений ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Абсциссы экспериментальных точек: ![x=[132, 140, 150, 162, 170, 180, 190, 200, 211, 220, 232, 240, 251]](https://intuit.ru//sites/default/files/tex_cache/21cdecf7a18a51334824d5d83da65be7.png) , ординаты:
, ординаты: ![y=[330, 350, 385, 425, 450, 485, 540, 600, 660, 730, 920, 1020, 1350]](https://intuit.ru//sites/default/files/tex_cache/dc5cc00b631ad8c77646b823e5546f57.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
Абсциссы экспериментальных точек: ![x=[-0.65, 0.99, 1.76, 1.1, -0.44, 1.42, 0.99, -0.04, -0.23, -0.86, 0.34, 0.89, -0.15, 1.2, 0.5, -0.26]](https://intuit.ru//sites/default/files/tex_cache/ce1898ce000352089ce36c0631920c3f.png) , ординаты:
, ординаты: ![y=[0.35, 0.61, 1.0, 0.18, 0.88, 0.97, 0.88, 0.74, 0.17, 0.79, 0.78, 0.96, 0.2, 0.09, 0.02, 0.3]](https://intuit.ru//sites/default/files/tex_cache/3473a957dccb43ceabde51855c860fe8.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
Подберите коэффициенты полинома 5-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 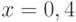 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 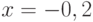 интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Вычислите значение выражения 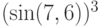 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 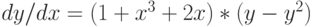 . Начальные условия
. Начальные условия 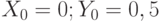 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Определить количество простых делителей числа  не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
Вычислите наименьшее общее кратное чисел 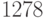 и
и  . Ответ -- целое число.
. Ответ -- целое число.
Организуйте решение методом Кутта-Мерсона дифференциального уравнения: 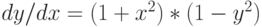 . Начальные условия
. Начальные условия 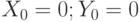 . Шаг 0,01, точность 0,001. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
. Шаг 0,01, точность 0,001. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
Вычислите вторую производную функции 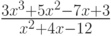 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке  . Ответ округлите до 1-го знака после запятой (в меньшую сторону).
. Ответ округлите до 1-го знака после запятой (в меньшую сторону).
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 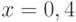 интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Даны матрицы ![A=[3,1,0; 7,8,9; 0,1,1]](https://intuit.ru//sites/default/files/tex_cache/cf0293da7507afca2494f9a85433e162.png) и
и ![B=[1,2,3; 0,1,1; 2,3,4]](https://intuit.ru//sites/default/files/tex_cache/382ad8c75ee46619b7d7bca351c2a660.png) . Решите матричное уравнение
. Решите матричное уравнение 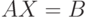 . В ответ запишите значение определителя полученной матрицы
. В ответ запишите значение определителя полученной матрицы  , округлив результат до одного знака после запятой.
, округлив результат до одного знака после запятой.
Найдите минимум функции  при ограничениях:
при ограничениях:  Ответ округлите до 2-го знака после запятой.
Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Адамса дифференциального уравнения: 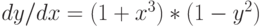 . Начальные условия
. Начальные условия 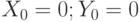 . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение 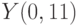 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Решите уравнение 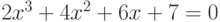 . Сложите значения всех корней. В ответ запишите действительную часть результа с точностью до целого.
. Сложите значения всех корней. В ответ запишите действительную часть результа с точностью до целого.
Выберите функцию, позволяющую строить гистограммы.
Постройте функции 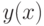 , заданные параметрически:
, заданные параметрически: 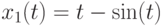 ,
,  и
и 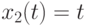 ,
, 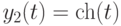 при
при ![t\in \[2, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/aff8ef137885fb948cb16ca6a8138655.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Дано выражение 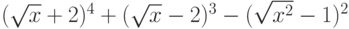 . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат.
Найдите произведение элементов вектора кумулятивного произведения элементов вектора ![[2:3:10]](https://intuit.ru//sites/default/files/tex_cache/077370dd41e5cd9d62b3e93211cb893c.png) . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите сумму корней уравнения 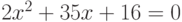 . Ответ округлить до 1-го знака после запятой (в меньшую сторону).
. Ответ округлить до 1-го знака после запятой (в меньшую сторону).
Постройте в полярной системе координат графики функций  и
и 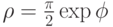 при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
Организуйте поиск минимума функции 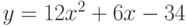 . В ответ запишите значение
. В ответ запишите значение  , при котором достигается минимум. Ответ округлите до 2-го знака после запятой (в меньшую сторону).
, при котором достигается минимум. Ответ округлите до 2-го знака после запятой (в меньшую сторону).
Постройте графики функций  и
и  . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число.
Даны координаты точек  ,
,  и
и  ,
, 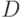 . Выберите четверки точек такие, что векторы
. Выберите четверки точек такие, что векторы  и
и 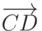 сонаправлены.
сонаправлены.
Вычислите производную функции 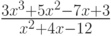 в технике символьных вычислений. Выберите ыерный ответ.
в технике символьных вычислений. Выберите ыерный ответ.
Выберите верное утверждение. Символ "%" (процент)
Даны векторы, заданные координатами начала и конца: 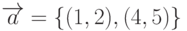 ,
, 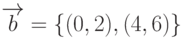 и
и 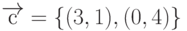 . Найдите длину вектора
. Найдите длину вектора 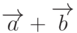 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Найдите минимум функции 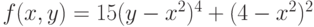 . Ответ округлите до целого.
. Ответ округлите до целого.
Постройте график функции  . Найдите количество локальных минимумов функции на отрезке
. Найдите количество локальных минимумов функции на отрезке ![\[ 0, 3\]](https://intuit.ru//sites/default/files/tex_cache/e749596926d59dbb4d3e9b8ba01b5ac6.png) . Ответ -- целое число.
. Ответ -- целое число.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 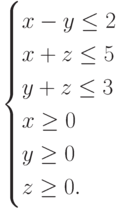 В ответ запишите значение функции
В ответ запишите значение функции  . Ответ округлите до целых.
. Ответ округлите до целых.
Подберите коэффициенты полинома 4-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 3-ой степени
. В ответе укажите коэффициент при 3-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.
Выберите верное утверждение. Символ ";" (точка с запятой)
Какая команда позволит обратить матрицу  ?
?
Вычислите определитель матрицы (ответ -- целое число):
| 0 | 2 | 6 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 6 | 3 | 4 | 2 |
Дана матрица. Найдите сумму элементов обратной к ней матрицы. Ответ округлите до двух знаков после запятой.
| 0 | 2 | 6 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 4 |
| 2 | 4 | 3 | 4 | 2 |
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (ответ округлите до двух знаков после запятой).
Вычислите значение выражения 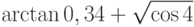 . В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
. В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
Вычислите значение выражения 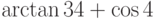 . Результат округлите до ближайшего целого в сторону нуля. Ответ -- целое число.
. Результат округлите до ближайшего целого в сторону нуля. Ответ -- целое число.
Вычислите наибольший общий делитель чисел 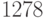 и
и  . Ответ -- целое число.
. Ответ -- целое число.
Даны три величины: 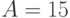 ,
,  и
и  . Найдите значение логического выражения
. Найдите значение логического выражения 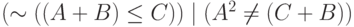 . Ответ -- целое число.
. Ответ -- целое число.
Дано выражение 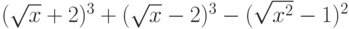 . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат.
Дана цепочка присвоений 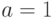 ,
, 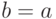 ,
,  . Какое значение будет хранить переменная
. Какое значение будет хранить переменная  ? Ответ -- целое число.
? Ответ -- целое число.
Какая из приведенных ниже точек (x,y) лежит внутри части плоскости, ограниченной линиями 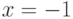 ,
, 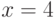 ,
,  ,
, 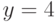 ?
?
Определить количество простых делителей числа 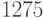 не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
Найдите количество символов в строке "Мой дядя самых честных правил, Когда не в шутку занемог, Он уважать себя заставил. И лучше выдумать не мог.", исключив пробелы и знаки препинания. Ответ -- целое число.
Реализуйте функцию, вычисляющую числа Фибоначчи (первые два числа -- единицы, каждое последующее равно сумме двух предыдущих). Вычислите 14-е число Фибоначчи. Ответ -- целое число.
Выберите функцию, возвращающую указатель на текущее графическое окно.
Выберите функцию, позволяющую устанавливать свойства графического объекта.
Даны матрицы ![M_{1}=[1,2,3;5,4,3;6,7,8]](https://intuit.ru//sites/default/files/tex_cache/57c3b4be070ea328d34473f411b584fc.png) и
и ![M_{2}=[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/960bc0723691bc60e235ec9800f0f72a.png) . Найдите сумму элементов 2-ой строки матрицы
. Найдите сумму элементов 2-ой строки матрицы 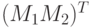 , (
, ( -- означает транспонирование). Ответ -- целое число.
-- означает транспонирование). Ответ -- целое число.
Найдите сумму элементов массива ![([1,3,4,5].^[2,4,6,8])(:)/[200]](https://intuit.ru//sites/default/files/tex_cache/d552a603a185b9c96b2d1694747be5cb.png) . Ответ округлите до целых.
. Ответ округлите до целых.
Решить систему линейных алгебраических уравнений, заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
| 5 | 5 | 7 | 1 | 6 | | 68 |
| 3 | 1 | 5 | 2 | 4 | | 48 |
| 2 | 4 | 3 | 2 | 3 | | 44 |
| 5 | 2 | 2 | 4 | 2 | | 55 |
| 2 | 3 | 6 | 3 | 1 | | 41 |
Даны векторы: 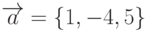 ,
, 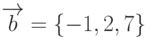 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов 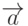 и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.
Уравнение прямой в параметрической форме имеет вид  . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью 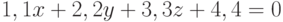 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Даны координаты точек: 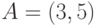 и
и 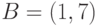 . Выберите параметрическое уравнение прямой, проходящей через эти точки.
. Выберите параметрическое уравнение прямой, проходящей через эти точки.
Даны два многочлена  и
и 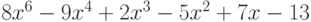 . Найдите сумму коэффициентов при степенях
. Найдите сумму коэффициентов при степенях  многочлена, получившегося в результате перемножения этих многочленов. Ответ -- целое число.
многочлена, получившегося в результате перемножения этих многочленов. Ответ -- целое число.
Выберите функцию, позволяющую разложить частное двух многочленов на простейшие рациональные дроби.
Решите систему уравнений: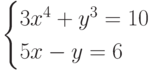 В ответ введите максимальное значение
В ответ введите максимальное значение  являющегося действительным корнем уравнения с точностью до 1-го знака после запятой.
являющегося действительным корнем уравнения с точностью до 1-го знака после запятой.
Вычислите третью производную функции 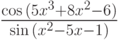 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 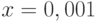 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Исследуйте функцию 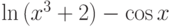 . На каком отрезке функция монотонно убывает?
. На каком отрезке функция монотонно убывает?
Вычислите по формуле Ньютона-Лейбница определенный интеграл 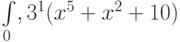 (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
Вычислите интеграл  методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Выберите функцию, реализующую численное интегрирование методом Симпсона.
Выберите функцию, реализующую численное интегрирование по квадратурным формулам Гаусса.
Организуйте решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Кутта-Мерсона дифференциального уравнения: 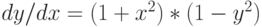 . Начальные условия
. Начальные условия 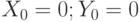 . Шаг 0,1, точность 0,01. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
. Шаг 0,1, точность 0,01. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
Организуйте решение методом Адамса дифференциального уравнения: 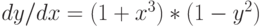 . Начальные условия
. Начальные условия 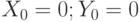 . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Организуйте решение методом Милна дифференциального уравнения: 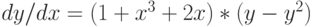 . Начальные условия
. Начальные условия 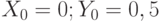 . Шаг 0,1. В ответ укажите значение
. Шаг 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите минимум функции  при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите такие значения переменных  ,
,  , при которых целевая функция
, при которых целевая функция 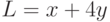 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 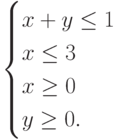 В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 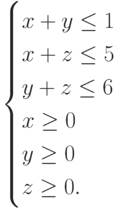 В ответ запишите максимальное значение
В ответ запишите максимальное значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Абсциссы экспериментальных точек: ![x=[0.16 0.73 0.94 0.76 0.25 0.85 0.73 0.4 0.33 0.07 0.53 0.7 0.36 0.79 0.58 0.32]](https://intuit.ru//sites/default/files/tex_cache/2dbd99d3dda7837af5b42c192c4cf90b.png) , ординаты:
, ординаты: ![y=[-0.65, 0.99, 1.76, 1.1, -0.44, 1.42, 0.99, -0.04, -0.23, -0.86, 0.34, 0.89, -0.15, 1.2, 0.5, -0.26]](https://intuit.ru//sites/default/files/tex_cache/28589f818f7db0f64757de87d10d2805.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
Подберите коэффициенты полинома 5-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 0-ой степени
. В ответе укажите коэффициент при 0-ой степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 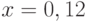 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 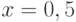 интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 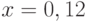 для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Найдите угол (в радианах) между плоскостями, заданными уравнениями 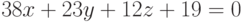 ,
, 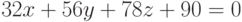 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Вычислите среднее арифметическое массива значений ![x=[0.35, 0.61, 1.0, 0.18, 0.88, 0.97, 0.88, 0.74, 0.17, 0.79, 0.78, 0.96, 0.2, 0.09, 0.02, 0.3]](https://intuit.ru//sites/default/files/tex_cache/c2b385cc28924af4571645a2f5f42c2b.png) . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите минимум функции  при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Организуйте решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите угол (в радианах) между плоскостями, заданными уравнениями 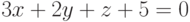 ,
, 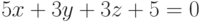 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Подберите коэффициенты полинома 4-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 3-ой степени
. В ответе укажите коэффициент при 3-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.
Вычислите след матрицы ![[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/385363aa456979c4891664829cfd5d99.png) . Ответ -- целое число.
. Ответ -- целое число.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 1-ой степени
. В ответе укажите коэффициент при 1-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Какая функция позволяет считать числа, записанные в файле 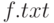 , в матрицу
, в матрицу 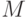 ?
?
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 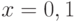 для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 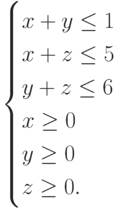 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Решите уравнение 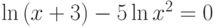 . Найдите сумму корней этого уравнения. Ответ округлить до 2-го знака после запятой.
. Найдите сумму корней этого уравнения. Ответ округлить до 2-го знака после запятой.
Дана матрица. Найдите сумму элементов обратной к ней матрицы. Ответ округлите до двух знаков после запятой.
| 1 | 2 | 5 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 4 | 4 | 0 |
Решить систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней (целое число).
Запишите число 2016 в виде двоичного числа, в таком виде, в каком оно хранится в памяти компьютера. В ответе запишите младшие 18 бит.
Вычислите значение выражения 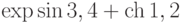 . В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
. В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
Дан массив 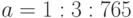 . Найти количество его нечетных элементов. Ответ -- целое число.
. Найти количество его нечетных элементов. Ответ -- целое число.
Постройте в полярной системе координат графики функций  и
и  при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Выберите функцию, возвращающую указатель на текущие оси графика.
Даны координаты точек  ,
,  и
и  ,
, 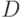 . Выберите четверки точек такие, что векторы
. Выберите четверки точек такие, что векторы  и
и 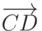 коллинеарны.
коллинеарны.
Найдите угол (в радианах) между плоскостями, заданными уравнениями  ,
, 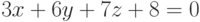 . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.
Даны координаты точек: 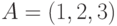 и
и  . Выберите уравнение прямой, проходящей через эти точки.
. Выберите уравнение прямой, проходящей через эти точки.
Выберите функцию, возвращающую частное и остаток от деления двух многочленов.
Даны два многочлена  и
и 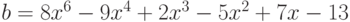 . Какова будет сумма коэффициентов при степенях
. Какова будет сумма коэффициентов при степенях  остаточного члена при разложении выражения
остаточного члена при разложении выражения 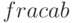 на простейшие дроби вида
на простейшие дроби вида 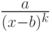 ?
?
Вычислите значение полинома 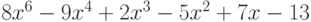 в точке
в точке 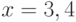 . В ответе приведите сумму коэффициентов при степенях
. В ответе приведите сумму коэффициентов при степенях  получившегося полинома. Ответ округлите до целого.
получившегося полинома. Ответ округлите до целого.
Корни алгебраического уравнения равны  ,
, 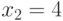 . Каков вид исходного уравнения?
. Каков вид исходного уравнения?
Решите систему уравнений: В ответ введите сумму значений корней переменной
В ответ введите сумму значений корней переменной  .
.
Вычислите производную функции 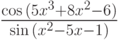 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 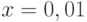 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Выберите функцию, реализующую численное интегрирование методом трапеций без накопления.
Вычислите интеграл  по квадратуре Гаусса. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
по квадратуре Гаусса. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
Организуйте решение модифицированным методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Организуйте решение с помощью встроенной функции  дифференциального уравнения:
дифференциального уравнения: 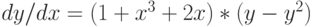 . Начальные условия
. Начальные условия 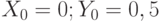 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 7-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 7-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
Выберите встроенную функцию, позволяющую решать задачи линейного программирования.
Найдите минимум функции  при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Вычислите среднее арифметическое массива значений ![x=[1:0.02:345]](https://intuit.ru//sites/default/files/tex_cache/426265edaac2adb8129e593560a93209.png) . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 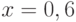 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Подберите коэффициенты полинома 3-ей степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Исследуйте функцию 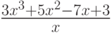 . На каком отрезке функция монотонно возрастает?
. На каком отрезке функция монотонно возрастает?
Выберите функцию, позволяющую вычислить производную от многочлена.
Найдите такие значения переменных  ,
,  , при которых целевая функция
, при которых целевая функция 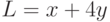 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 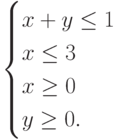 В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.
Вычислите значение интеграла от полинома  в точке
в точке 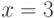 (постоянная интегрирования равна
(постоянная интегрирования равна 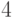 ). Ответ округлите до целого.
). Ответ округлите до целого.
Вычислите значение выражения 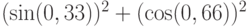 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой.
Реализуйте функцию  Вычислите
Вычислите  . Ответ -- целое число.
. Ответ -- целое число.
Вычислите значение выражения  . В ответ запишите значение аргумента полученного комплексного числа, округленное до двух знаков после запятой.
. В ответ запишите значение аргумента полученного комплексного числа, округленное до двух знаков после запятой.
Решите уравнение 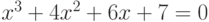 . Сложите значения всех корней. В ответ запишите действительную часть результата, округленную до целых.
. Сложите значения всех корней. В ответ запишите действительную часть результата, округленную до целых.
Задан массив 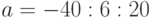 . В ответ запишите сумму первого и седьмого элементов данного массива (целое число).
. В ответ запишите сумму первого и седьмого элементов данного массива (целое число).
С какий позиции в строку "Мой дядя самых честных правил, Когда не в шутку занемог, Он уважать себя заставил. И лучше выдумать не мог." входит слово "шутку"? Ответ -- целое число.
Выберите функцию, предназначенную для вывода текста в заданной пользователем точке в графическом окне.
Даны векторы-строки ![a=[5,4,3,2,1,0]](https://intuit.ru//sites/default/files/tex_cache/a682f10c56ac154a3064a2d68aae4e9d.png) ,
, ![b=[1,2,3,4,5,6]](https://intuit.ru//sites/default/files/tex_cache/feb7135344cdf59ef73a3da4c843272c.png) ,
, ![c=[2,4,6,8,10,12]](https://intuit.ru//sites/default/files/tex_cache/149020042e8669f7bb2052f1237269bf.png) . Проведите вертикальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
. Проведите вертикальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
Дана матрица ![M=[1,2,3,4,5;5,4,3,2,1;6,7,8,9,0;0,9,8,7,6;9,7,5,4,3]](https://intuit.ru//sites/default/files/tex_cache/c3da0038a7e9419ffbc1015439c5ba31.png) . Найдите сумму элементов массива
. Найдите сумму элементов массива 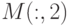 . Ответ -- целое число.
. Ответ -- целое число.
Дана матрица ![[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/385363aa456979c4891664829cfd5d99.png) . Приведите её к треугольному виду методом исключения Гаусса и вычислите сумму элементов второй строки получившейся матрицы. Ответ округлите до целого.
. Приведите её к треугольному виду методом исключения Гаусса и вычислите сумму элементов второй строки получившейся матрицы. Ответ округлите до целого.
Вычислите по формуле Ньютона-Лейбница определенный интеграл 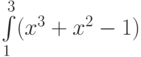 (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
Организуйте решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,2. В ответе укажите значение
. Шаг 0,2. В ответе укажите значение 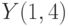 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.
Организуйте решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.
Найдите минимум функции 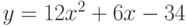 . Ответ округлите до 2-го знака после запятой (в меньшую сторону).
. Ответ округлите до 2-го знака после запятой (в меньшую сторону).
Найдите такие значения переменных  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 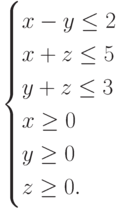 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых.
Подберите коэффициенты полинома 5-ой степени методом наименьших квадратов. Абсциссы экспериментальных точек: ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 5-ой степени
. В ответе укажите коэффициент при 5-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 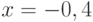 интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 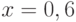 интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
Постройте графики функций  и
и  . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число.
Даны векторы-строки ![a=[5,4,3,2,1,0]](https://intuit.ru//sites/default/files/tex_cache/a682f10c56ac154a3064a2d68aae4e9d.png) ,
, ![b=[1,2,3,4,5,6]](https://intuit.ru//sites/default/files/tex_cache/feb7135344cdf59ef73a3da4c843272c.png) ,
, ![c=[2,4,6,8,10,12]](https://intuit.ru//sites/default/files/tex_cache/149020042e8669f7bb2052f1237269bf.png) . Проведите горизонтальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
. Проведите горизонтальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
В каком случае команда  позволит вывести результат предыдущей операции?
позволит вывести результат предыдущей операции?
Реализуйте функцию  Вычислите
Вычислите 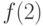 . Ответ -- целое число.
. Ответ -- целое число.
Дан массив 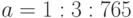 . Найти сумму его четных элементов. Ответ -- целое число.
. Найти сумму его четных элементов. Ответ -- целое число.
Вычислите интеграл  методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
Вычислите среднее арифметическое массива значений ![x=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/3a0262f0cbfd81fef0a3791691772a16.png) . Ответ запишите с точностью до 1-го знака после запятой.
. Ответ запишите с точностью до 1-го знака после запятой.
Дана экспериментальная зависимость. Абсциссы экспериментальных точек: ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
Вычислите интеграл 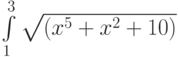 методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.
Реализуйте функцию, вычисляющую числа Фибоначчи (первые два числа -- единицы, каждое последующее равно сумме двух предыдущих). Вычислите 12-е число Фибоначчи. Ответ -- целое число.
Вычислите определитель матрицы (ответ -- целое число):
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
Задан массив 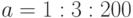 . В ответ запишите длину данного массива (целое число).
. В ответ запишите длину данного массива (целое число).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. Ответ -- целое число.
Выберите функцию, реализующую численное интегрирование методом трапеций c накоплением.
Абсциссы экспериментальных точек: ![x=[1, 2, 3, 4, 5, 6, 7]](https://intuit.ru//sites/default/files/tex_cache/f2489f2f675d3822dde3ac785a1622a7.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
Укажите отличие в работе операторов  и
и  ?
?
Выберите функцию, предназначенную для вывода текста под осью 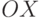 .
.
Какие из приведенных ниже команд позволяют продолжать ввод выражения более чем на одной строке?
Постройте функции 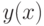 , заданные параметрически:
, заданные параметрически: 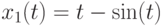 ,
,  и
и 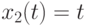 ,
, 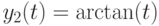 при
при ![t\in \[1, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/3d65c999c76c6e6a7fdfb6dc61b07348.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
Даны матрицы ![M_{1}=[1,2,3;5,4,3;6,7,8]](https://intuit.ru//sites/default/files/tex_cache/57c3b4be070ea328d34473f411b584fc.png) и
и ![M_{2}=[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/960bc0723691bc60e235ec9800f0f72a.png) . Найдите сумму элементов 3-его столбца матрицы
. Найдите сумму элементов 3-его столбца матрицы 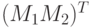 , (
, ( -- означает транспонирование). Ответ -- целое число.
-- означает транспонирование). Ответ -- целое число.
Даны векторы: 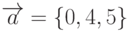 ,
,  . Найдите угол между векторами
. Найдите угол между векторами  и
и  в радианах. Ответ округлить до 1-го знака после запятой.
в радианах. Ответ округлить до 1-го знака после запятой.
![[2:3:10]](https://intuit.ru//sites/default/files/tex_cache/077370dd41e5cd9d62b3e93211cb893c.png) . Ответ округлите до целых.
. Ответ округлите до целых.  , позволяющее добавлять в конец непустого текстового файла информацию и считывать её.
, позволяющее добавлять в конец непустого текстового файла информацию и считывать её.  , где
, где  -- файл, в который производилась запись информации?
-- файл, в который производилась запись информации? 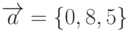 ,
, 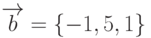 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов 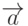 и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.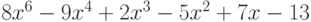 в точке
в точке  (постоянная интегрирования нулевая). Ответ округлите до целого.
(постоянная интегрирования нулевая). Ответ округлите до целого. 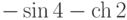 . Результат округлите до ближайшего целого в сторону отрицательной бесконечности. Ответ -- целое число.
. Результат округлите до ближайшего целого в сторону отрицательной бесконечности. Ответ -- целое число.  по квадратуре Гаусса. Точность -- по умолчанию. В ответ записать количество итераций, за которое был вычислен интеграл (целое число).
по квадратуре Гаусса. Точность -- по умолчанию. В ответ записать количество итераций, за которое был вычислен интеграл (целое число). ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 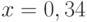 для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.![A=[3,1,0; 2,5,6; 0,1,1]](https://intuit.ru//sites/default/files/tex_cache/6615ab7a5beae0d0bab93d8b20d4d951.png) и
и ![B=[1,2,3; 0,1,1; 2,3,4]](https://intuit.ru//sites/default/files/tex_cache/382ad8c75ee46619b7d7bca351c2a660.png) . Решите матричное уравнение
. Решите матричное уравнение 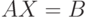 . В ответ запишите значение определителя полученной матрицы
. В ответ запишите значение определителя полученной матрицы  , округлив результат до одного знака после запятой.
, округлив результат до одного знака после запятой. 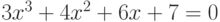 . Сложите значения всех корней. В ответ запишите действительную часть результата с точностью до 2-х знаков после запятой.
. Сложите значения всех корней. В ответ запишите действительную часть результата с точностью до 2-х знаков после запятой. 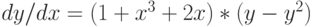 . Начальные условия
. Начальные условия 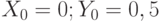 . Шаг 0,01. В ответ укажите значение
. Шаг 0,01. В ответ укажите значение 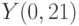 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 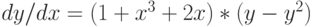 . Начальные условия
. Начальные условия 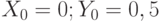 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 8-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 8-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой. . Найдите количество локальных максимумов функции на отрезке
. Найдите количество локальных максимумов функции на отрезке ![\[ 0, 3\]](https://intuit.ru//sites/default/files/tex_cache/e749596926d59dbb4d3e9b8ba01b5ac6.png) . Ответ -- целое число.
. Ответ -- целое число. 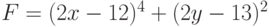 при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых. 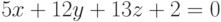 ,
,  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой. ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 4-ой степени
. В ответе укажите коэффициент при 4-ой степени  . Ответ округлите до 3-го знака после запятой.
. Ответ округлите до 3-го знака после запятой.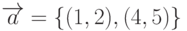 ,
, 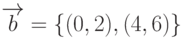 и
и 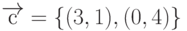 . Найдите длину вектора
. Найдите длину вектора 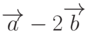 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.  . Найдите сумму действительных частей корней этого уравнения. Ответ округлить до целых в меньшую сторону.
. Найдите сумму действительных частей корней этого уравнения. Ответ округлить до целых в меньшую сторону. 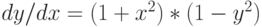 . Начальные условия
. Начальные условия 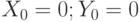 . Шаг 0,1, точность 0,1. В ответ укажите значение
. Шаг 0,1, точность 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. и
и 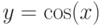 . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число. 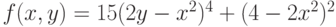 . В ответ запишите значение
. В ответ запишите значение  , при котором достигается минимум. Ответ округлите до 2-го знака после запятой.
, при котором достигается минимум. Ответ округлите до 2-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 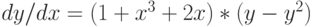 . Начальные условия
. Начальные условия 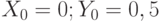 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.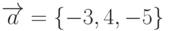 ,
, 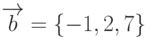 . Найдите угол между векторами
. Найдите угол между векторами  и
и  в радианах. Ответ округлить до 1-го знака после запятой.
в радианах. Ответ округлить до 1-го знака после запятой. 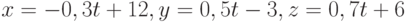 . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью 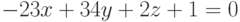 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. 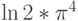 . В ответе запишите действительную часть числа, округленную до четырех знаков после запятой (использовать обычное округление).
. В ответе запишите действительную часть числа, округленную до четырех знаков после запятой (использовать обычное округление). 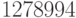 нацело делится на число
нацело делится на число  . Результат сложите с остатком от деления этих чисел. Ответ -- целое число.
. Результат сложите с остатком от деления этих чисел. Ответ -- целое число. 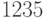 , не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
, не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.  . Найдите количество локальных минимумов функции на отрезке
. Найдите количество локальных минимумов функции на отрезке ![\[ 3, 6\]](https://intuit.ru//sites/default/files/tex_cache/e85becbdfa3b398fb43c646ea2fe0498.png) . Ответ -- целое число.
. Ответ -- целое число.  и
и 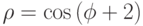 при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число. 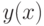 , заданные параметрически:
, заданные параметрически: 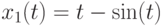 ,
,  и
и 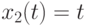 ,
,  при
при ![t\in \[0, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/fd1fe5dda34ed5256fcc066c0350c1dc.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число. ![M=[1,2,3,4,5;5,4,3,2,1;6,7,8,9,0;0,9,8,7,6;9,7,5,4,3]](https://intuit.ru//sites/default/files/tex_cache/c3da0038a7e9419ffbc1015439c5ba31.png) . Преобразуйте матрицу следующим образом:
. Преобразуйте матрицу следующим образом: ![M(1:3, 3:4)=[1,1;2,2;4,5]](https://intuit.ru//sites/default/files/tex_cache/7e4b9b9b9b20508535e48a1755d058fb.png) . Найдите сумму элементов массива
. Найдите сумму элементов массива 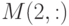 . Ответ -- целое число.
. Ответ -- целое число. ![M_{1}=[1,2,3;5,4,3;6,7,8]](https://intuit.ru//sites/default/files/tex_cache/57c3b4be070ea328d34473f411b584fc.png) и
и ![M_{2}=[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/960bc0723691bc60e235ec9800f0f72a.png) . Найдите сумму элементов 1-ой строки матрицы
. Найдите сумму элементов 1-ой строки матрицы 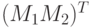 , (
, ( -- означает транспонирование). Ответ -- целое число.
-- означает транспонирование). Ответ -- целое число. 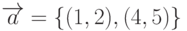 ,
, 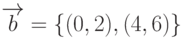 и
и 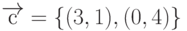 . Найдите длину вектора
. Найдите длину вектора  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.  ,
, 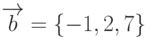 . Найдите угол между векторами
. Найдите угол между векторами  и
и  в радианах. Ответ округлить до 1-го знака после запятой.
в радианах. Ответ округлить до 1-го знака после запятой. 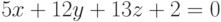 ,
, 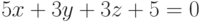 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.  ,
, 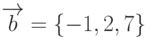 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов  и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой. 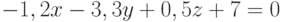 ,
,  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой. 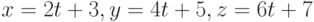 . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.  . В ответе приведите сумму коэффициентов при степенях
. В ответе приведите сумму коэффициентов при степенях  получившегося полинома. Ответ -- целое число.
получившегося полинома. Ответ -- целое число. 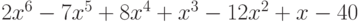 в точке
в точке  (постоянная интегрирования равна
(постоянная интегрирования равна  ). Ответ округлите до целого.
). Ответ округлите до целого.  . Найдите сумму действительных частей корней этого уравнения. Ответ округлить до 2-го знака после запятой (в меньшую сторону).
. Найдите сумму действительных частей корней этого уравнения. Ответ округлить до 2-го знака после запятой (в меньшую сторону). 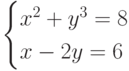 В ответ введите значение действительного корня
В ответ введите значение действительного корня  с точностью до 2-го знака после запятой.
с точностью до 2-го знака после запятой. 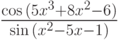 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 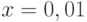 . Ответ округлите до 1-го знака после запятой (в меньшую сторону).
. Ответ округлите до 1-го знака после запятой (в меньшую сторону).  (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой. 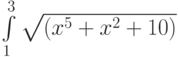 методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.  методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.  методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение 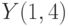 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой. . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение 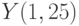 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.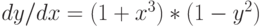 . Начальные условия
. Начальные условия 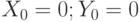 . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.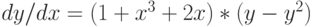 . Начальные условия
. Начальные условия 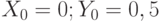 . Шаг 0,1. В ответ укажите значение
. Шаг 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 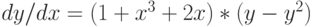 . Начальные условия
. Начальные условия 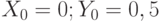 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 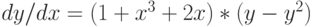 . Начальные условия
. Начальные условия 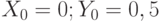 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение 5-го от начала узла, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой. при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. 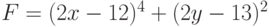 при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.  ,
,  , при которых целевая функция
, при которых целевая функция 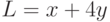 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 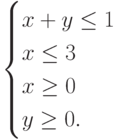 В ответ запишите максимальное значение
В ответ запишите максимальное значение  . Ответ округлите до целых.
. Ответ округлите до целых.  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 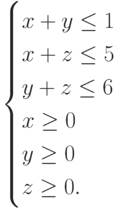 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых.  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 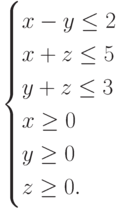 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых. ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до 3-го знака после запятой.
. Ответ округлите до 3-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 4-ой степени
. В ответе укажите коэффициент при 4-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.![x=[132, 140, 150, 162, 170, 180, 190, 200, 211, 220, 232, 240, 251]](https://intuit.ru//sites/default/files/tex_cache/21cdecf7a18a51334824d5d83da65be7.png) , ординаты:
, ординаты: ![y=[330, 350, 385, 425, 450, 485, 540, 600, 660, 730, 920, 1020, 1350]](https://intuit.ru//sites/default/files/tex_cache/dc5cc00b631ad8c77646b823e5546f57.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.![x=[-0.65, 0.99, 1.76, 1.1, -0.44, 1.42, 0.99, -0.04, -0.23, -0.86, 0.34, 0.89, -0.15, 1.2, 0.5, -0.26]](https://intuit.ru//sites/default/files/tex_cache/ce1898ce000352089ce36c0631920c3f.png) , ординаты:
, ординаты: ![y=[0.35, 0.61, 1.0, 0.18, 0.88, 0.97, 0.88, 0.74, 0.17, 0.79, 0.78, 0.96, 0.2, 0.09, 0.02, 0.3]](https://intuit.ru//sites/default/files/tex_cache/3473a957dccb43ceabde51855c860fe8.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до целого.
. Ответ округлите до целого.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 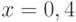 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 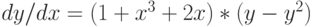 . Начальные условия
. Начальные условия 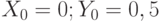 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 6-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой. не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число. 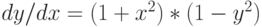 . Начальные условия
. Начальные условия 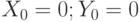 . Шаг 0,01, точность 0,001. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
. Шаг 0,01, точность 0,001. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.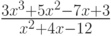 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке  . Ответ округлите до 1-го знака после запятой (в меньшую сторону).
. Ответ округлите до 1-го знака после запятой (в меньшую сторону). ![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 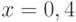 интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![A=[3,1,0; 7,8,9; 0,1,1]](https://intuit.ru//sites/default/files/tex_cache/cf0293da7507afca2494f9a85433e162.png) и
и ![B=[1,2,3; 0,1,1; 2,3,4]](https://intuit.ru//sites/default/files/tex_cache/382ad8c75ee46619b7d7bca351c2a660.png) . Решите матричное уравнение
. Решите матричное уравнение 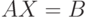 . В ответ запишите значение определителя полученной матрицы
. В ответ запишите значение определителя полученной матрицы  , округлив результат до одного знака после запятой.
, округлив результат до одного знака после запятой. 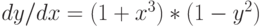 . Начальные условия
. Начальные условия 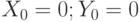 . Шаг 0,01. В ответе укажите значение
. Шаг 0,01. В ответе укажите значение 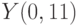 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.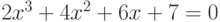 . Сложите значения всех корней. В ответ запишите действительную часть результа с точностью до целого.
. Сложите значения всех корней. В ответ запишите действительную часть результа с точностью до целого. 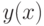 , заданные параметрически:
, заданные параметрически: 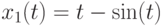 ,
,  и
и 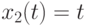 ,
, 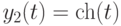 при
при ![t\in \[2, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/aff8ef137885fb948cb16ca6a8138655.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число. ![[2:3:10]](https://intuit.ru//sites/default/files/tex_cache/077370dd41e5cd9d62b3e93211cb893c.png) . Ответ округлите до целых.
. Ответ округлите до целых.  и
и 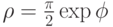 при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число. 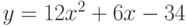 . В ответ запишите значение
. В ответ запишите значение  , при котором достигается минимум. Ответ округлите до 2-го знака после запятой (в меньшую сторону).
, при котором достигается минимум. Ответ округлите до 2-го знака после запятой (в меньшую сторону). и
и  . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число. 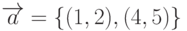 ,
, 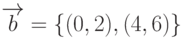 и
и 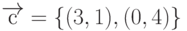 . Найдите длину вектора
. Найдите длину вектора 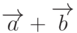 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.  . Найдите количество локальных минимумов функции на отрезке
. Найдите количество локальных минимумов функции на отрезке ![\[ 0, 3\]](https://intuit.ru//sites/default/files/tex_cache/e749596926d59dbb4d3e9b8ba01b5ac6.png) . Ответ -- целое число.
. Ответ -- целое число. ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 2-ой степени
. В ответе укажите коэффициент при 2-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого. ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 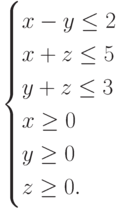 В ответ запишите значение функции
В ответ запишите значение функции  . Ответ округлите до целых.
. Ответ округлите до целых. ![x=[1,2,3,4,5,6,7]](https://intuit.ru//sites/default/files/tex_cache/ba121b6f2432bd804157fc5c4638faa8.png) , ординаты:
, ординаты: ![y=[3.1, 2.2, 3.2, 7.0, 1.2, 5.4, 4.3]](https://intuit.ru//sites/default/files/tex_cache/81950fe2a431e1f9db6162deb0c16430.png) . В ответе укажите коэффициент при 3-ой степени
. В ответе укажите коэффициент при 3-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.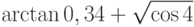 . В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
. В ответе запишите действительную часть числа, округленную до трех знаков после запятой. 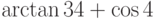 . Результат округлите до ближайшего целого в сторону нуля. Ответ -- целое число.
. Результат округлите до ближайшего целого в сторону нуля. Ответ -- целое число. 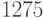 не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число.
не превышающих его. Простое число делится без остатка только на единицу и на само себя. Ответ -- целое число. ![M_{1}=[1,2,3;5,4,3;6,7,8]](https://intuit.ru//sites/default/files/tex_cache/57c3b4be070ea328d34473f411b584fc.png) и
и ![M_{2}=[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/960bc0723691bc60e235ec9800f0f72a.png) . Найдите сумму элементов 2-ой строки матрицы
. Найдите сумму элементов 2-ой строки матрицы 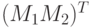 , (
, ( -- означает транспонирование). Ответ -- целое число.
-- означает транспонирование). Ответ -- целое число. 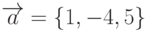 ,
, 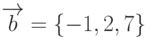 . Найти длину вектора, полученного в результате векторного произведения векторов
. Найти длину вектора, полученного в результате векторного произведения векторов  и
и  . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.  . Найдите угол (в радианах) между прямой и плоскостью
. Найдите угол (в радианах) между прямой и плоскостью 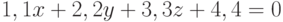 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.  и
и 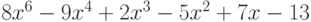 . Найдите сумму коэффициентов при степенях
. Найдите сумму коэффициентов при степенях  многочлена, получившегося в результате перемножения этих многочленов. Ответ -- целое число.
многочлена, получившегося в результате перемножения этих многочленов. Ответ -- целое число. 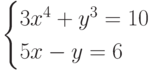 В ответ введите максимальное значение
В ответ введите максимальное значение  являющегося действительным корнем уравнения с точностью до 1-го знака после запятой.
являющегося действительным корнем уравнения с точностью до 1-го знака после запятой. 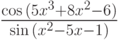 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 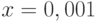 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. 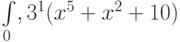 (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.  методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.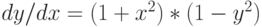 . Начальные условия
. Начальные условия 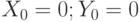 . Шаг 0,1, точность 0,01. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.
. Шаг 0,1, точность 0,01. В ответе укажите значение количество пройденных итераций. Ответ -- целое число.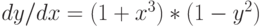 . Начальные условия
. Начальные условия 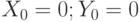 . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.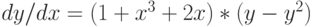 . Начальные условия
. Начальные условия 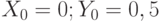 . Шаг 0,1. В ответ укажите значение
. Шаг 0,1. В ответ укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.  ,
,  , при которых целевая функция
, при которых целевая функция 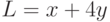 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 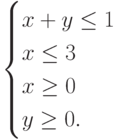 В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.  ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 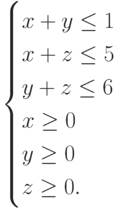 В ответ запишите максимальное значение
В ответ запишите максимальное значение  . Ответ округлите до целых.
. Ответ округлите до целых. ![x=[0.16 0.73 0.94 0.76 0.25 0.85 0.73 0.4 0.33 0.07 0.53 0.7 0.36 0.79 0.58 0.32]](https://intuit.ru//sites/default/files/tex_cache/2dbd99d3dda7837af5b42c192c4cf90b.png) , ординаты:
, ординаты: ![y=[-0.65, 0.99, 1.76, 1.1, -0.44, 1.42, 0.99, -0.04, -0.23, -0.86, 0.34, 0.89, -0.15, 1.2, 0.5, -0.26]](https://intuit.ru//sites/default/files/tex_cache/28589f818f7db0f64757de87d10d2805.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до целого.
. Ответ округлите до целого.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 0-ой степени
. В ответе укажите коэффициент при 0-ой степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 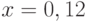 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 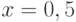 интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 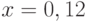 для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.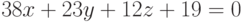 ,
, 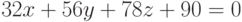 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой.  при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.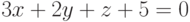 ,
, 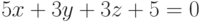 . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой. ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент при 3-ой степени
. В ответе укажите коэффициент при 3-ой степени  . Ответ запишите с точностью до 2-го знака после запятой.
. Ответ запишите с точностью до 2-го знака после запятой.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 1-ой степени
. В ответе укажите коэффициент при 1-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для линейного сплайна. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой. ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 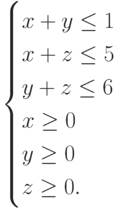 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых. 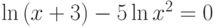 . Найдите сумму корней этого уравнения. Ответ округлить до 2-го знака после запятой.
. Найдите сумму корней этого уравнения. Ответ округлить до 2-го знака после запятой. 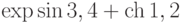 . В ответе запишите действительную часть числа, округленную до трех знаков после запятой.
. В ответе запишите действительную часть числа, округленную до трех знаков после запятой.  и
и  при
при ![\phi \in \[ \frac{-\pi}{4}, \frac{\pi}{4}\]](https://intuit.ru//sites/default/files/tex_cache/bd16ba6830bee0a2d1d0c81c488861b8.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.  ,
, 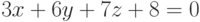 . Ответ округлить до 1-го знака после запятой.
. Ответ округлить до 1-го знака после запятой.  и
и 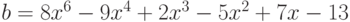 . Какова будет сумма коэффициентов при степенях
. Какова будет сумма коэффициентов при степенях  остаточного члена при разложении выражения
остаточного члена при разложении выражения 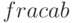 на простейшие дроби вида
на простейшие дроби вида 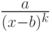 ?
? 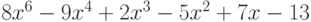 в точке
в точке 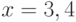 . В ответе приведите сумму коэффициентов при степенях
. В ответе приведите сумму коэффициентов при степенях  получившегося полинома. Ответ округлите до целого.
получившегося полинома. Ответ округлите до целого. 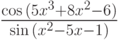 . В ответ запишите значение полученной функции в точке
. В ответ запишите значение полученной функции в точке 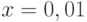 . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой.  по квадратуре Гаусса. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
по квадратуре Гаусса. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой. дифференциального уравнения:
дифференциального уравнения: 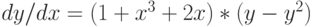 . Начальные условия
. Начальные условия 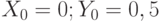 . Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования
. Начальный шаг 0,1, максимальный -- 0,2. Интервал интегрирования ![\[0,1\]](https://intuit.ru//sites/default/files/tex_cache/134e042df5e079aeca1c3d6a26bb5741.png) . В ответе укажите значение полученной функции в 7-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой.
. В ответе укажите значение полученной функции в 7-ом от начала узле, в котором ищется решение (исходная точка -- первый узел). Ответ округлите до 2-го знака после запятой. при ограничениях:
при ограничениях:  В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых. ![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.
. В ответе укажите коэффициент корреляции. Ответ округлите до 3-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 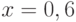 канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.
канонического интерполяционного полинома. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[1.802, 4.246, 3.67, 1.955, 5.25, 2.588]](https://intuit.ru//sites/default/files/tex_cache/7d7b52b74c0eb7da389fa0c2cf4b53e3.png) . В ответе укажите коэффициент при 3-ей степени
. В ответе укажите коэффициент при 3-ей степени  . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой. ,
,  , при которых целевая функция
, при которых целевая функция 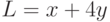 достигает своего максимального значения при ограничениях:
достигает своего максимального значения при ограничениях: 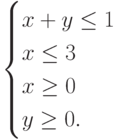 В ответ запишите значение переменной
В ответ запишите значение переменной  . Ответ округлите до целых.
. Ответ округлите до целых.  в точке
в точке 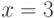 (постоянная интегрирования равна
(постоянная интегрирования равна 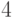 ). Ответ округлите до целого.
). Ответ округлите до целого.  . В ответ запишите значение аргумента полученного комплексного числа, округленное до двух знаков после запятой.
. В ответ запишите значение аргумента полученного комплексного числа, округленное до двух знаков после запятой. 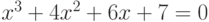 . Сложите значения всех корней. В ответ запишите действительную часть результата, округленную до целых.
. Сложите значения всех корней. В ответ запишите действительную часть результата, округленную до целых. ![a=[5,4,3,2,1,0]](https://intuit.ru//sites/default/files/tex_cache/a682f10c56ac154a3064a2d68aae4e9d.png) ,
, ![b=[1,2,3,4,5,6]](https://intuit.ru//sites/default/files/tex_cache/feb7135344cdf59ef73a3da4c843272c.png) ,
, ![c=[2,4,6,8,10,12]](https://intuit.ru//sites/default/files/tex_cache/149020042e8669f7bb2052f1237269bf.png) . Проведите вертикальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
. Проведите вертикальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число. ![[1:3:7;1:2:6;4:5:15]](https://intuit.ru//sites/default/files/tex_cache/385363aa456979c4891664829cfd5d99.png) . Приведите её к треугольному виду методом исключения Гаусса и вычислите сумму элементов второй строки получившейся матрицы. Ответ округлите до целого.
. Приведите её к треугольному виду методом исключения Гаусса и вычислите сумму элементов второй строки получившейся матрицы. Ответ округлите до целого. 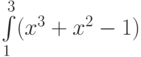 (постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.
(постоянная интегрирования нулевая). Ответ округлите до 1-го знака после запятой.  . Начальные условия
. Начальные условия  . Шаг 0,2. В ответе укажите значение
. Шаг 0,2. В ответе укажите значение 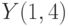 . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе укажите значение
. Шаг 0,1. В ответе укажите значение  . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. ,
,  ,
,  , при которых целевая функция
, при которых целевая функция  достигает своего минимального значения при ограничениях:
достигает своего минимального значения при ограничениях: 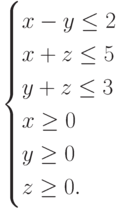 В ответ запишите значение
В ответ запишите значение  . Ответ округлите до целых.
. Ответ округлите до целых. ![x=[0.053, 0.705, 0.624, 0.204, 0.824, 0.421]](https://intuit.ru//sites/default/files/tex_cache/095d7134512afa4b5acc86d6c42a2040.png) , ординаты:
, ординаты: ![y=[-19.236, 15.031, 7.926, -15.577, 27.156, -6.077]](https://intuit.ru//sites/default/files/tex_cache/8f99034aa583cd587646d06d755f9436.png) . В ответе укажите коэффициент при 5-ой степени
. В ответе укажите коэффициент при 5-ой степени  . Ответ округлите до целого.
. Ответ округлите до целого.![x=[-0.12, 0.54, 0.231, 1.23]](https://intuit.ru//sites/default/files/tex_cache/870e5a93f067dda0889906372f2d6d2e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341]](https://intuit.ru//sites/default/files/tex_cache/28d00fb73f601d6288d86cf6c85af97d.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Лагранжа. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке 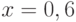 интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой.
для кубического сплайна. Ответ запишите с точностью до 2-го знака после запятой. и
и  . Найдите количество точек пересечения этих функций на отрезке
. Найдите количество точек пересечения этих функций на отрезке ![\[ -0,5, 1\]](https://intuit.ru//sites/default/files/tex_cache/21b0b7ef7d52e6525367b42a0e5948e0.png) . Ответ -- целое число.
. Ответ -- целое число. ![a=[5,4,3,2,1,0]](https://intuit.ru//sites/default/files/tex_cache/a682f10c56ac154a3064a2d68aae4e9d.png) ,
, ![b=[1,2,3,4,5,6]](https://intuit.ru//sites/default/files/tex_cache/feb7135344cdf59ef73a3da4c843272c.png) ,
, ![c=[2,4,6,8,10,12]](https://intuit.ru//sites/default/files/tex_cache/149020042e8669f7bb2052f1237269bf.png) . Проведите горизонтальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.
. Проведите горизонтальную конкатенацию этих векторов. Укажите количество элементов в первой строке получившегося массива. Ответ -- целое число.  методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой.
методом Симпсона. Точность -- по умолчанию. Ответ округлить до 2-го знака после запятой. ![x=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/3a0262f0cbfd81fef0a3791691772a16.png) . Ответ запишите с точностью до 1-го знака после запятой.
. Ответ запишите с точностью до 1-го знака после запятой.![x=[-0.12, 0.54, 0.231, 1.23, 1.74, 2.123, 2.012, 3.78, 4.001]](https://intuit.ru//sites/default/files/tex_cache/f507be6ce76805fd15d63203789ee78e.png) , ординаты:
, ординаты: ![y=[-1.876, -1.231, -0.96, -0.341, 0.002, 0.081, 0.21, 0.471, 0.671]](https://intuit.ru//sites/default/files/tex_cache/faf7294e075c78f160888d552084baf1.png) . В ответе укажите ожидаемое значение в точке
. В ответе укажите ожидаемое значение в точке  интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.
интерполяционного полинома Ньютона. Ответ запишите с точностью до 2-го знака после запятой.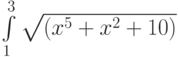 методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом
методом трапеций без накопления. Интервал интегрирования делите на отрезки с шагом  . Ответ округлить до 2-го знака после запятой.
. Ответ округлить до 2-го знака после запятой. 
![([1,3,4,5].*[2,4,6,8])(:)(2)](https://intuit.ru//sites/default/files/tex_cache/4f2641dc01fd8f1f159a73428bfd355f.png) . Ответ округлите до целых.
. Ответ округлите до целых.  . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат. 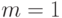 . Какие из приведенных ниже команд вернут значение
. Какие из приведенных ниже команд вернут значение  ,
, 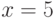 ,
,  ,
, 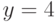 ?
? ![([1,3,4,5]./[2,4,6,8])(:)(2)](https://intuit.ru//sites/default/files/tex_cache/0d1e8579c4d5abb06144d67c19280390.png) . Ответ округлите до целых.
. Ответ округлите до целых.  ,
,  и
и  ,
,  . Выберите четверки точек такие, что векторы
. Выберите четверки точек такие, что векторы  и
и  коллинеарны.
коллинеарны. 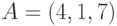 и
и  . Выберите параметрическое уравнение прямой, проходящей через эти точки.
. Выберите параметрическое уравнение прямой, проходящей через эти точки.  на
на  ?
? 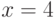 ,
,  ,
,  ?
?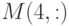 . Ответ -- целое число.
. Ответ -- целое число. 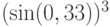 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой. . Модуль результата округлите до четырех знаков после запятой.
. Модуль результата округлите до четырех знаков после запятой. 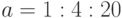 . В ответ запишите сумму всех его элементов (целое число).
. В ответ запишите сумму всех его элементов (целое число).  Вычислите
Вычислите  . Ответ -- целое число.
. Ответ -- целое число.  . Найти сумму его нечетных элементов. Ответ -- целое число.
. Найти сумму его нечетных элементов. Ответ -- целое число.  . Ответ -- целое число.
. Ответ -- целое число. 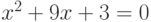 . Ответ округлить до целых в меньшую сторону.
. Ответ округлить до целых в меньшую сторону. 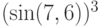 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой.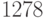 и
и  . Ответ -- целое число.
. Ответ -- целое число. 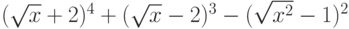 . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат. 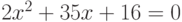 . Ответ округлить до 1-го знака после запятой (в меньшую сторону).
. Ответ округлить до 1-го знака после запятой (в меньшую сторону). 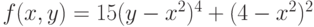 . Ответ округлите до целого.
. Ответ округлите до целого.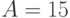 ,
,  и
и  . Найдите значение логического выражения
. Найдите значение логического выражения 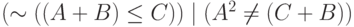 . Ответ -- целое число.
. Ответ -- целое число. 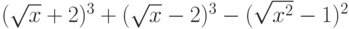 . Раскройте скобки. Выберите верный результат.
. Раскройте скобки. Выберите верный результат. 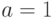 ,
, 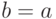 ,
,  . Какое значение будет хранить переменная
. Какое значение будет хранить переменная 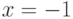 ,
, ![([1,3,4,5].^[2,4,6,8])(:)/[200]](https://intuit.ru//sites/default/files/tex_cache/d552a603a185b9c96b2d1694747be5cb.png) . Ответ округлите до целых.
. Ответ округлите до целых. 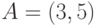 и
и 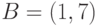 . Выберите параметрическое уравнение прямой, проходящей через эти точки.
. Выберите параметрическое уравнение прямой, проходящей через эти точки. 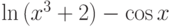 . На каком отрезке функция монотонно убывает?
. На каком отрезке функция монотонно убывает? ![x=[0.35, 0.61, 1.0, 0.18, 0.88, 0.97, 0.88, 0.74, 0.17, 0.79, 0.78, 0.96, 0.2, 0.09, 0.02, 0.3]](https://intuit.ru//sites/default/files/tex_cache/c2b385cc28924af4571645a2f5f42c2b.png) . Ответ округлите до 2-го знака после запятой.
. Ответ округлите до 2-го знака после запятой. , в матрицу
, в матрицу  ?
? 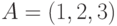 и
и  . Выберите уравнение прямой, проходящей через эти точки.
. Выберите уравнение прямой, проходящей через эти точки.  ,
, 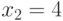 . Каков вид исходного уравнения?
. Каков вид исходного уравнения?  В ответ введите сумму значений корней переменной
В ответ введите сумму значений корней переменной ![x=[1:0.02:345]](https://intuit.ru//sites/default/files/tex_cache/426265edaac2adb8129e593560a93209.png) . Ответ округлите до 1-го знака после запятой.
. Ответ округлите до 1-го знака после запятой.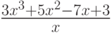 . На каком отрезке функция монотонно возрастает?
. На каком отрезке функция монотонно возрастает? 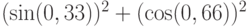 . Ответ округлите до двух знаков после запятой.
. Ответ округлите до двух знаков после запятой. Вычислите
Вычислите  . Ответ -- целое число.
. Ответ -- целое число. 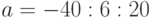 . В ответ запишите сумму первого и седьмого элементов данного массива (целое число).
. В ответ запишите сумму первого и седьмого элементов данного массива (целое число). 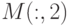 . Ответ -- целое число.
. Ответ -- целое число.  позволит вывести результат предыдущей операции?
позволит вывести результат предыдущей операции?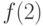 . Ответ -- целое число.
. Ответ -- целое число. 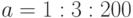 . В ответ запишите длину данного массива (целое число).
. В ответ запишите длину данного массива (целое число). ![x=[1, 2, 3, 4, 5, 6, 7]](https://intuit.ru//sites/default/files/tex_cache/f2489f2f675d3822dde3ac785a1622a7.png) , ординаты:
, ординаты: 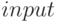 и
и  ?
?  .
. 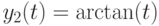 при
при ![t\in \[1, 2\pi\]](https://intuit.ru//sites/default/files/tex_cache/3d65c999c76c6e6a7fdfb6dc61b07348.png) . Найдите количество точек пересечения графиков этих функций. Ответ -- целое число.
. Найдите количество точек пересечения графиков этих функций. Ответ -- целое число. 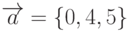 ,
,  . Найдите угол между векторами
. Найдите угол между векторами