Чему равен параметр P формулы 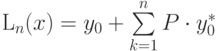 , полученной в результате свертки формулы Ньютона?
, полученной в результате свертки формулы Ньютона?
(Отметьте один правильный вариант ответа.)
Варианты ответа
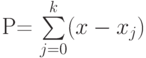

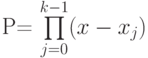 (Верный ответ)
(Верный ответ)


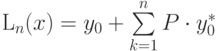 , полученной в результате свертки формулы Ньютона?
, полученной в результате свертки формулы Ньютона?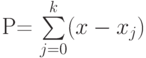

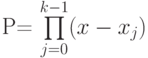 (Верный ответ)
(Верный ответ)

 и требуемым среднеквадратичным отклонением
и требуемым среднеквадратичным отклонением 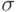 для двенадцати (k=12) равномерно распределенных случайных величин?
для двенадцати (k=12) равномерно распределенных случайных величин?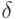 ?
?