Если среди базисных компонентов псевдоплана x нет отрицательных, то псевдоплан x={xi0} является:
(Отметьте один правильный вариант ответа.)
Варианты ответа
оптимальным решением прямой задачи(Верный ответ)
оптимальным решением двойственной задачи
допустимым решением прямой задачи

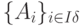 соответствует псевдоплан
соответствует псевдоплан 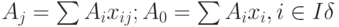 Тогда для базисных компонентов справедливо условие:
Тогда для базисных компонентов справедливо условие: