Введение в математическое программирование

<<- Назад к вопросам

Размерность дна оврага определяется числом малых собственных значений матрицы

Варианты ответа

Гессе(Верный ответ)

производных

Стьюдента

Похожие вопросы

Если штраф создает барьер из больших значений Р вдоль границы допустимой области, эти методы называются...?

В каком из методов происходит сравнение значений функции в (n + 1) вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры?

Для табличного симплекс – метода в качестве начального базиса выбран базис из свободных переменных, для которых c_i = 0. Соответствующее значение целевой функции определяется соотношением a₀₀ = Σc_ix_i = 0, i є I. Тогда оценки для всех небазисных переменных равны:

Если для табличного симплекс – метода в качестве начального базиса выбирают базис из свободных переменных, для которых ci = 0, и оценки для всех небазисных переменных равны Δ_j=a_0j=-c_j, то соответствующее значение целевой функции определяется соотношением:

Пусть ограничения задачи линейного программирования записаны в виде: A₁x₁+A₂x₂+...+A_nx_n+A_n+1x_n+1+...+A_n+mx_n+m=A₀, где А₁,...,А_m – множество линейно независимых векторов. Согласно симплекс – метода, базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ определяется уравнением:

Если значения целевой функции прямой задачи никогда не превышают значений целевой функции двойственной задачи, т.е. c^Tx₀≤b^Ty₀, то допустимые решения прямой и двойственной задач имеют вид:

Пусть задача линейного программирования задана в канонической форме: максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0. Предположим, что n ≥ m и ранг матрицы A равен m. Тогда двойственная задача имеет вид:

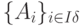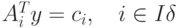Сопряженным базисом называется такая система из m линейно - независимых векторов матрицы ограничений прямой задачи $\{ A_i \}_{i \in I \delta}$ , для которой базисное решение y соответствующей системы линейных уравнений вида $A^T_i y = c_i, \quad i \in I \delta$ , удовлетворяет ограничениям:

Пусть задана задача нелинейного программирования: минимизировать f(x₁,...,x_n) при условиях

h₁(x₁,...,x_n) = 0;h₂(x₁,...,x_n) = 0;...............h_m(x₁,...,x_n) = 0.

Допустим, что существует такая точка x*, в которой достигается относительный экстремум данной задачи. Если ранг матрицы I = [δh_j(x)/δx_j], i = 1,...,m; j = 1,...,n в точке x* равен m, то существуют m чисел λ₁,...,λ_n, не все из которых равны нулю одновременно, и при которых:

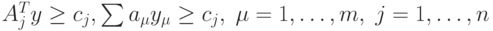Пусть некоторое базисное решение y системы линейных уравнений вида $A^T_i y = c_i, \quad i \in I \delta$ , удовлетворяет ограничениям $A^T_j y \ge c_j, \sum a_{\mu}y_{\mu} \ge c_j, \; \mu = 1,\ldots,m, \; j = 1,\ldots,n$ Тогда вектора матрицы ограничений прямой задачи $\{ A_i \}_{i \in I \delta}$ , составляющие сопряженный базис, являются: