Линейная разностная задача устойчива, если для любого значения 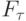 она имеет единственное решение
она имеет единственное решение 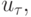 причём
причём
(Отметьте один правильный вариант ответа.)
Варианты ответа
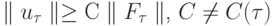
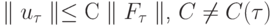
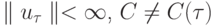

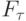 она имеет единственное решение
она имеет единственное решение 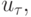 причём
причём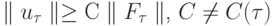
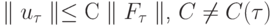
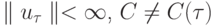
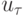 - решение разностного уравнения, а
- решение разностного уравнения, а 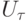 - проекция точного решения на разностную сетку. Решение
- проекция точного решения на разностную сетку. Решение 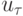 сходится к решению при
сходится к решению при 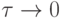 , если:
, если: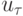 сходится к решению при
сходится к решению при 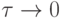 и имеет место оценка
и имеет место оценка 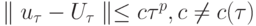 , то сходимость имеет порядок
, то сходимость имеет порядок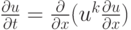 , а также граничные условия:
, а также граничные условия:  . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 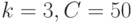
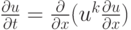 , а также граничные условия:
, а также граничные условия: 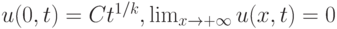 . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 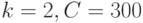 :
: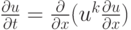 . Какой вид приобретет данное уравнение в переменных бегущей волны
. Какой вид приобретет данное уравнение в переменных бегущей волны  ?
?