Введение в численные методы решения квазилинейных уравнений параболического типа - ответы
Количество вопросов - 81
В теореме Лакса-Рябенького порядок аппроксимации и порядок сходимости
Чем необходимо дополнить одномерное линейное уравнение теплопроводности для решения задачи?
Какой размер имеют электроды в схеме установки плазменного переключателя тока?
Если в дифференциальной задаче выполняется закон сохранения и соответствующий закон сохранения выполняется и на сеточном уровне, то разностная схема
Плазменная задача считается более трудной из-за наличия:
Каким дифференциальным уравнением будут определяться свойства автомодельных решений?
Безусловноустойчивой разностной схемой для многомерного уравнения теплопроводности является
Роль неавтомодельных точных решений не выяснена, но очевидно, что она
В случае термоядерного горения в уравнениях для упрощенной модели появится:
Метод построения автомодельных решений, основанный на использовании преобразований растяжения-сжатия, носит название
Метод прогонки используется в неявной схеме с нелинейностью на нижнем слое для
Если из соотношений следует в смысле выбранной нормы, что то разностная задача является
Режим с обострением формируется в результате действия механизма
Что необходимо задать для того, чтобы смешанная задача для уравнения параболического типа была корректно поставленной?
Если коэффициент теплопроводности зависит от времени и координат, то интегро-интерполяционный метод позволяет получить
Если решение дифференциального уравнения зависит не от двух переменных t и x, а от их комбинаций, то оно является
Методы подобия и размерности опираются на
Если в дифференциальной задаче имеется несколько законов сохранения, а при переходе к сеточному описанию все они получаются как следствия выбранной разностной схемы, в результате алгебраических преобразований, то схема называется
Стоки в нелинейной среде будут возникать
Метод дробных шагов, предложенный Н.Н.Яненко также называется
Если решение разностного уравнения 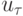 сходится к решению при
сходится к решению при 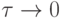 и имеет место оценка
и имеет место оценка 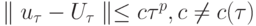 , то сходимость имеет порядок
, то сходимость имеет порядок
Чему пропорционален обмен энергией между электронами и ионами в задаче о динамике высокотемпературной плазмы?
Порядок аппроксимации локально-одномерной схемы в трёхмерном случае равен:
Методы построения точных решений опираются на две основы
В каких переменных ищется решение квазилинейных уравнений?
Чем отличаются особи, конкурирующие за субстрат?
Наличие нелинейности в коэффициенте теплопроводности является проявлением:
Какие стандарты применяются для решения задачи о динамике высокотемпературной плазмы?
При отсутствии магнитного поля в выражении для электронного теплового потока останется слагаемое, содержащее:
Каким образом получают плазменную перемычку в схеме установки плазменного переключателя тока?
Какими будут производные в плазменной задаче при наличии нелинейности?
По теореме Лакса-Рябенького: если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы:
Если линейно-разностная задача линейно устойчива и аппроксимирует дифференциальную задачу на ее решении, то решение линейной разностной задачи:
В уравнения для упрощенной модели течения с постоянной по пространству плотностью входит разность:
Пусть 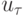 - решение разностного уравнения, а
- решение разностного уравнения, а 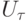 - проекция точного решения на разностную сетку. Решение
- проекция точного решения на разностную сетку. Решение 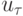 сходится к решению при
сходится к решению при 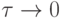 , если:
, если:
Линейная разностная задача устойчива, если для любого значения 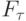 она имеет единственное решение
она имеет единственное решение 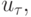 причём
причём
Чем необходимо дополнить одномерное линейное уравнение теплопроводности для решения задачи?
При использовании неявной схемы с нелинейностью на нижнем слое, решение в верхнем слое по времени находится с помощью
Если коэффициент теплопроводности зависит от времени и координат, то консервативную схему можно получить, используя следующий метод
Схема переменных направлений для многомерного уравнения теплопроводности является
Проведите повышение порядка аппроксимации схемы до четвертого на нерасширенном шаблоне и укажите вид добавочного члена в правой части разностого уравнения
В уравнение теплопроводности входит пять величин. Сколько из этих пяти величин имеют независимую размерность?
Если имеется запись физического закона, зависящая от k переменых, r из которых имеют независимую переменную, то данную зависимость можно представить в безразмерном виде как уравнение зависящее от
На каком расстоянии от начала горения остановится тепловая волна в однородной среде при наличии стока?
Фундаментальное решение оператора теплопроводности
Порядок аппроксимации локально-одномерной схемы в двумерном случае равен:
Какие необходимо использовать разностные схемы, чтобы можно было решать квазилинейные уравнения?
Задано квазилинейное уравнение вида 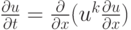 . Какой вид приобретет данное уравнение в переменных бегущей волны
. Какой вид приобретет данное уравнение в переменных бегущей волны  ?
?
Точные решения уравнения теплопроводности находятся с использованием
Релаксационный параметр в задаче о динамике высокотемпературной плазмы пропорционален электронной температуре в степени:
Из представленного списка переменных укажите независимые:
Автомодельным является решение, зависящее не от двух переменных t и x, а от
Задано квазилинейное уравнение вида 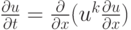 , а также граничные условия:
, а также граничные условия:  . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 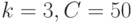
Задано квазилинейное уравнение вида 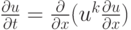 , а также граничные условия:
, а также граничные условия: 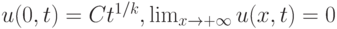 . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 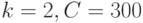 :
:
Решения типа бегущей волны являются
При реализации схемы с нелинейностью в верхнем слое итерации продолжаются до выполнения условия:
Укажите возможные способы повышения порядка аппроксимации:
Режим с обострением - динамический закон, при котором одна или несколько моделируемых величин за конечный промежуток времени
Расстояние между электродами в схеме установки плазменного переключателя выбирается равным:
Какие физические процессы описываются с помощью параболических уравнений?
Множество дискретных решений по сравнению с множеством дифференциальных уравнений
Какие уравнения используются для описания математической модели динамики высокотемпературной плазмы?
Задано уравнение параболического типа и начальное условие. Что необходимо задать ещё для того, чтобы соответствующая задача была корректно поставлена?
Разностная схема называется консервативной, если:
Неявные схемы используют уравнения, которые выражают данные:
Численное решение простейших диффернциальных уравнений параболического типа сильно усложняется, если
Если используется одна безразмерная комбинация, то сколько будет автомодельных решений?
Что наблюдается в реальности вместо ухода в бесконечность для режима с обострением?
Какие условия накладывается на функцию 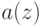 , входящую в квазилинейное параболическое уравнение вида
, входящую в квазилинейное параболическое уравнение вида ![\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}[a(u)\frac{\partial u}{\partial t}]+f(u)](https://intuit.ru//sites/default/files/tex_cache/538ba20153fbe4fe409b7662080f2499.png) ?
?
Какие классы точных решений, описываемые обыкновенными дифференциальными уравнениями, являются наиболее простыми
Разностная задача является устойчивой, если из соотношений следует в смысле выбранной нормы, что
В принципе Гаузе самый приспособленный вид:
Решение линейно-разностной задачи сходится к решению дифференциальной задачи, если разностная задача:
Что помогает найти П-теорема?
Интегро-интерполяционный метод позволяет получить консервативную схему, если
В нелинейной среде за счет стоков могут образовываться
Пусть в дифференциальной задаче выполняется некий закон сохранения. Для того, чтобы разностная схема была консервативной, необходимо, чтобы
В одномерном линейном уравнении теплопроводности:
Какими будут производные в экологической задаче при наличии нелинейности
При решении нелинейного уравнения теплопроводности может быть использовано
Нестационарное решение уравнения можно найти, используя стационарное решение, в котором добавить

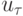 сходится к решению при
сходится к решению при 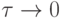 и имеет место оценка
и имеет место оценка 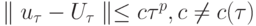 , то сходимость имеет порядок
, то сходимость имеет порядок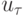 - решение разностного уравнения, а
- решение разностного уравнения, а 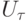 - проекция точного решения на разностную сетку. Решение
- проекция точного решения на разностную сетку. Решение 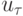 сходится к решению при
сходится к решению при 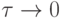 , если:
, если: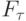 она имеет единственное решение
она имеет единственное решение 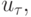 причём
причём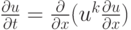 . Какой вид приобретет данное уравнение в переменных бегущей волны
. Какой вид приобретет данное уравнение в переменных бегущей волны  ?
?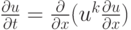 , а также граничные условия:
, а также граничные условия:  . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 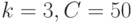
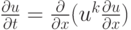 , а также граничные условия:
, а также граничные условия: 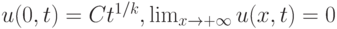 . Вычислите скорость фронта тепловой волны при
. Вычислите скорость фронта тепловой волны при 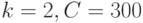 :
: