Если раскрыть скобки в бесконечном произведении 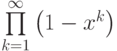 , чему равен коэффициент при
, чему равен коэффициент при 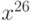 ?
?
(Ответ необходимо ввести в поле ввода.)
Варианты ответа

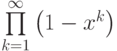 , чему равен коэффициент при
, чему равен коэффициент при 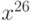 ?
? вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 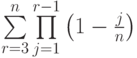 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) Чему равна асимптотическая оценка
Чему равна асимптотическая оценка 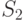 ?
? вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 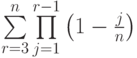 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) Чему равна асимптотическая оценка
Чему равна асимптотическая оценка 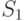 ?
? вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 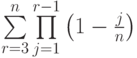 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) .При указанном интервале суммирования для
.При указанном интервале суммирования для 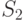 , что является нижней оценкой величины
, что является нижней оценкой величины 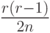 ?
? вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 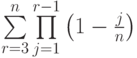 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки 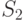
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина 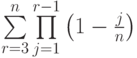 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки 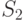
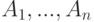 - события. Пусть
- события. Пусть 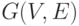 произвольный орграф зависимостей. И существуют
произвольный орграф зависимостей. И существуют  , что выполняется
, что выполняется 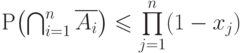 . Что верно относительно
. Что верно относительно  ?
?