База ответов ИНТУИТ

Дискретный анализ и теория вероятностей

<<- Назад к вопросам

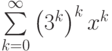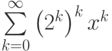Если говорить о \sum\limits_{k=0}^{\infty}\left( 3^k\right)^k x^k и \sum\limits_{k=0}^{\infty}\left( 2^k\right)^k x^k как о формальных степенных рядах, какие из перечисленных утверждений являются верными?

(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
радиус сходимости равен 1
ряды различаются(Верный ответ)
радиус сходимости равен 0(Верный ответ)
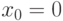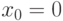при x_0=0 равны 1(Верный ответ)
ряды совпадают
Похожие вопросы
Если говорить о \sum\limits_{k=0}^{\infty}\left( 3^k\right)^k x^k и \sum\limits_{k=0}^{\infty}\left( 2^k\right)^k x^k как о производящих функциях, какие из перечисленных утверждений являются верными?
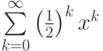Найдите радиус сходимости ряда \sum\limits_{k=0}^{\infty}\left( \frac 1 2 \right) ^k x^k, и выберите какие из перечисленных утверждений являются верными?
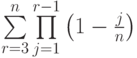При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с n вершинами и циклом, построенным на r вершинах, величина \sum\limits_{r=3}^{n}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)заменяется на сумму двух слагаемых S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right).При указанном интервале суммирования для S_2, 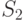что является нижней оценкой величины \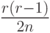frac{r(r-1)}{2n}?
При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с n вершинами и циклом, построенным на r вершинах, величина \sum\limits_{r=3}^{n}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)заменяется на сумму двух слагаемых S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)Чему равна асимптотическая оценка S_2?
При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с n вершинами и циклом, построенным на r вершинах, величина \sum\limits_{r=3}^{n}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)заменяется на сумму двух слагаемых S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)Чему равна асимптотическая оценка S_1?
При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с n вершинами и циклом, построенным на r вершинах, величина \sum\limits_{r=3}^{n}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)заменяется на сумму двух слагаемых S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right).Выберите операции и свойства, которые использовались для нахождения асимптотической оценки S_2
При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с n вершинами и циклом, построенным на r вершинах, величина \sum\limits_{r=3}^{n}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)заменяется на сумму двух слагаемых S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right).Выберите операции и свойства, которые использовались для нахождения асимптотической оценки S_2
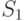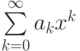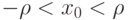Говорят, что степенной ряд \sum\limits_{k=0}^{\infty}a_k x^k сходится в точке x_0, если -\rho<x_0<\rho, где радиус ряда \rho=\frac{1}{\varlimsup\limits_{k\to\infty}{\sqrt[k]{|a_k|}}}>|x_0|Это утверждение является...
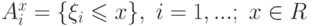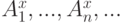Пусть случайное событие определено так A_i^x=\{\xi_i\leqslant x\},\ i=1,...;\ x\in R. Имеется A_1^x,...,A_n^x,... бесконечная последовательность событий. Тогда к чему 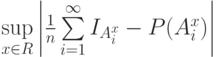\sup\limits_{x\in R}\left|\frac 1 n \sum\limits_{i=1}^{\infty}I_{A_i^x}-P(A_i^x)\right | сходится почти наверное?
Говорят, что степенной ряд \sum\limits_{k=0}^{\infty}a_k x^k сходится в точке x_0, если радиус ряда \rho=\frac{1}{\varlimsup\limits_{k\to\infty}{\sqrt[k]{|a_k|}}}>|x_0|Это утверждение является...