Задано дифференциальное уравнение второго порядка с переменными коэффициентами:  , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
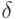
.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
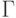
, если:
Дана задача Коши для дифференциального уравнения: 
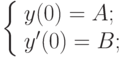
Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 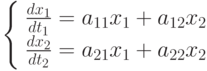
Найдите корень характеристического уравнения.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Определите кратность корней характеристического уравнения (1 или 2).
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

,

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

. В ответе привести три цифры после десятичной запятой.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

, если:
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
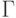
, если:
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
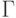
, если:
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора
.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Дана система дифференциальных уравнений: 
Определите кратность корней характеристического уравнения (1 или 2).
Дана система дифференциальных уравнений: 
Найдите корень характеристического уравнения.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Определите кратность корней характеристического уравнения (1 или 2).
Дана система дифференциальных уравнений: 
Найдите корень характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
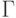
, если:
Дана система дифференциальных уравнений: 
Найдите корень характеристического уравнения.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
, если:
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
, если:
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 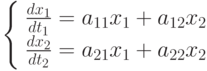
Определите кратность корней характеристического уравнения (1 или 2).
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора
.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Дана система дифференциальных уравнений: 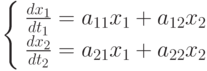 Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана система дифференциальных уравнений: 
Определите кратность корней характеристического уравнения (1 или 2).
Дана система дифференциальных уравнений: 
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана система дифференциальных уравнений: 
Найдите дискриминант характеристического уравнения.
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
Условия. Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать, сколько корней имеет решение в диапазоне

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
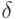
.
Дана система дифференциальных уравнений: 
Определите кратность корней характеристического уравнения (1 или 2).
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

. В ответе привести три цифры после десятичной запятой.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
Дана система дифференциальных уравнений: 
Найдите корень характеристического уравнения.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки: . Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана задача Коши для дифференциального уравнения: 

Показать, что решение имеет вид:

А также, что решение может быть представлено в виде:

Найти сколько корней имеет решение в диапазоне

и

и

. В ответе указать значение

. В ответе привести три цифры после десятичной запятой.
Дано характеристическое уравнение: 
| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение

.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
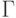
, если:
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора

.
Дана система дифференциальных уравнений: 
Рассмотрите фазовую плоскость:

, где

(

– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

, где

. В ответе укажите значение

.
Дано характеристическое уравнение: 
| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
Составить матрицу Гурвица и вычислить значение главного диагонального минора
.
Дана система дифференциальных уравнений: 
Найдите корень характеристического уравнения.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
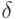
.
Дана система дифференциальных уравнений: 
Показать, что первыми интегралами системы являются выражения вида:

В ответе указать значение
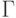
, если:
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: , где
, где
Найти решение с помощью подстановки:

. Показать, что решение имеет вид:

. В ответе укажите значение

.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.



 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 В ответе указать значение
В ответе указать значение 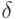 .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 В ответе указать значение
В ответе указать значение 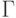 , если:
, если: 
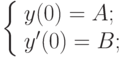
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.
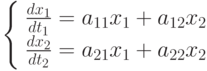


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.

 .
.

 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.


 .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне 
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  , если:
, если: 
 В ответе указать значение
В ответе указать значение 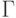 , если:
, если:  В ответе указать значение
В ответе указать значение 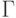 , если:
, если: 
 .
.

 .
.

 .
.

 .
.

 .
.

 .
.

 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.




 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 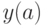 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 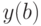 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 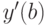 .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.



 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.

 .
.


 В ответе указать значение
В ответе указать значение  .
.

 .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.

 В ответе указать значение
В ответе указать значение 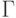 , если:
, если:  Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.


 В ответе указать значение
В ответе указать значение  .
.

 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
 В ответе указать значение
В ответе указать значение 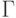 , если:
, если:  Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение 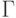 , если:
, если: 
 .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.
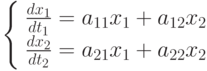
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение  .
.

 .
.

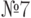 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.

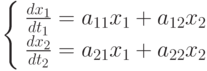 Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат. 

 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 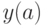 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 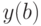 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 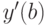 .
.


 .
.

 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение дискриминанта характеристического уравнения.

 .
.

 В ответе указать значение
В ответе указать значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.

 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 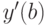 .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать, сколько корней имеет решение в диапазоне
. В ответе указать, сколько корней имеет решение в диапазоне  .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 В ответе указать значение
В ответе указать значение 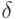 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 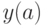 .
.



 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наибольшего из корней характеристического уравнения.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: . В ответе укажите значение
. В ответе укажите значение  .
.

 , где
, где  , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.

 .
.

 .
.


 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:  Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  . В ответе указать значение
. В ответе указать значение  . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.

 .
.

 В ответе указать значение
В ответе указать значение  .
.

 В ответе указать значение
В ответе указать значение 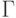 , если:
, если: 
 .
.

 , где
, где  (
( – корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы). В ответе указать значение наименьшего из корней характеристического уравнения.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение 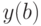 .
.
 Для дифференциального уравнения:
Для дифференциального уравнения: .
. 
 . В ответе указать значение
. В ответе указать значение  .
.
 , где
, где  . Показать, что решение имеет вид:
. Показать, что решение имеет вид: , где
, где  . В ответе укажите значение
. В ответе укажите значение  .
.

 .
.


 В ответе указать значение
В ответе указать значение 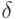 .
.

 В ответе указать значение
В ответе указать значение  , если:
, если: 