Классические и квантовые вычисления

Следовая норма оператора $A\in\LL(\calN)$ равна:

(Отметьте один правильный вариант ответа.)

Варианты ответа

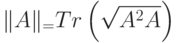
$\|A\|_\trr=Tr\left(\sqrt{A^2 A}\right)$

$\|A\|_\trr=Tr\left(\sqrt{A^\dagger}\right)$

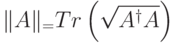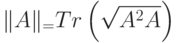
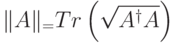$\|A\|_\trr=Tr\left(\sqrt{A^\dagger A}\right)$ (Верный ответ)

Похожие вопросы

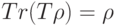Если имеется физически реализуемое преобразование $T\colon\LL(\calN)\to\LL(\calM)$ , причем для любого чистого состояния $\rho$ выполняется свойство: $Tr_{\calF}(T\rho)=\rho$ , то для любого оператора

справедливым является равенство ( $\gamma$ - некоторая фиксированная матрица плотности на пространстве $\calF$ ):

При отображении $\LL(\calN)$ в $\LL(\calN\otimes\calK)$ , $\calN$ - квантовая часть и $\calK$ - классическая часть системы, результат является диагональным по отношению:

Пусть $\calN=\bigoplus_{j}\calN_j$ - разложение пространства $\calN$ в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности $\rho$ , $\gamma$

Если имеется чистое состояние $\ket{\psi}\in\calN\otimes\calF$ , то разложение Шмидта имеет вид ( $0<\lambda_j\le 1$ , $\{\ket{\xi_j}\}\subset\calN$ и $\{\ket{\eta_j}\}\subset\calF$ - ортонормированные вектора):

Верно ли, что если применить измеряющий оператор к состоянию $\ket0\bra0\otimes\rho$ , где $\rho\double\in\LL(\calN)$ , то вероятность наблюдения состояния

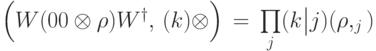можно записать в виде: $\PP\Bigl(W(\ket0\bra0\otimes\rho)W^\dagger,\,\CC(\ket{k})\otimes\calN\Bigr) \,=\, \prod\limits_{j} \PP(k\big| j) \PP(\rho, \calL_j)$ ?

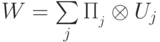Как называется оператор вида $W=\sum\limits_{j}^{} \Pi_{\calL_j}\otimes U_j$ , если в пространстве состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ ?

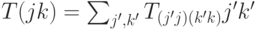Каким условиям эквивалентна физическая реализуемость линейного оператора $T\colon\LL(\calN)\to\LL(\calM)$ , записанного в координатном виде $T(\ket{j}\bra{k})=\sum_{j',k'} T_{(j'j)(k'k)} \ket{j'}\bra{k'}$ ?

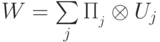Если есть пространство состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ , тогда всякий оператор вида $W=\sum\limits_{j}^{} \Pi_{\calL_j}\otimes U_j$ будет называться:

Если есть пространство состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ , тогда измеряющим будет называться всяки оператор вида:

Если применить измеряющий оператор к состоянию $\ket0\bra0\otimes\rho$ , где $\rho\double\in\LL(\calN)$ , то вероятность наблюдения состояния

можно записать в виде:

Классические и квантовые вычисления

Следовая норма оператора равна:

Следовая норма оператора $A\in\LL(\calN)$ равна: