По какому правилу в квантовой постановке действует оракул, задающий оператор 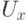 :
:
(Отметьте один правильный вариант ответа.)
Варианты ответа
 (Верный ответ)
(Верный ответ)
нет верного ответа


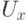 :
: (Верный ответ)
(Верный ответ)

 - множество троек вида
- множество троек вида  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
(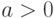 ,
,  - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 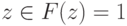 выполняется:
выполняется: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), то задаваемый изоморфизм имеет вид:
), то задаваемый изоморфизм имеет вид: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  ,
,  соответствует повороту вокруг оси X на:
соответствует повороту вокруг оси X на: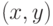 на квантовой схеме, означает, что:
на квантовой схеме, означает, что: и
и 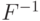 , чтобы
, чтобы  реализовалась обратимой схемой размера
реализовалась обратимой схемой размера 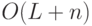 :
: ,
, 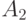 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 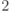 - их нулевые подпространства, причем
- их нулевые подпространства, причем 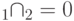 , ненулевые собственные числа
, ненулевые собственные числа  и
и 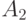 не меньше
не меньше 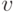 , где
, где 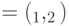 - угол между
- угол между  и
и 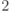 , то справедливым является равенство:
, то справедливым является равенство: