Каким вектором можно дополнить систему векторов: 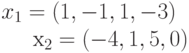 до ортогонального базиса?
до ортогонального базиса?
(Отметьте один правильный вариант ответа.)
Варианты ответа
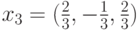
 (Верный ответ)
(Верный ответ)
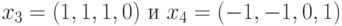

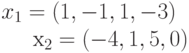 до ортогонального базиса?
до ортогонального базиса?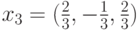
 (Верный ответ)
(Верный ответ)
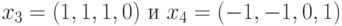
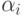 - угол между вектором
- угол между вектором 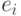 и подпространством W, то
и подпространством W, то 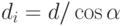 ?
?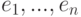 - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе  , где
, где 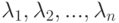 ?
?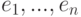 - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе 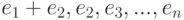 ?
?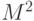 задано скалярное произведение
задано скалярное произведение  . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
. Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора 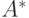 в базисе
в базисе  ?
?