Нелинейные вычислительные процессы

Укажите разностную схему при произвольном временном шаге интегрирования для данного уравнения: ${u_t} = {\varepsilon _1}{u_{xx}} + {\varepsilon _2}{u_{yy}}$

(Отметьте один правильный вариант ответа.)

Варианты ответа

${\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots$

$h(\vec U_m^{n + 1/2} - \vec U_m^{n - 1/2}) - [(B{{\vec U}_x})_{m + 1/2}^n - (B{{\vec U}_x})_{m - 1/2}^n]\tau = 0$

$(1 + \frac{1}{{2\varepsilon }}\sum\limits_j {{\alpha _{{k_j}}}} X_j^2)U_k^{n + 1} = (\frac{1}{{2\varepsilon }}\sum\limits_j {X_j^2{\alpha _{{k_j}}})U_k^n + } \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} }$ (Верный ответ)

Похожие вопросы

Является ли явной данная разностная схема? $(1 + \frac{1}{{2\varepsilon }}\sum\limits_j {{\alpha _{{k_j}}}} X_j^2)U_k^{n + 1} = (\frac{1}{{2\varepsilon }}\sum\limits_j {X_j^2{\alpha _{{k_j}}})U_k^n + } \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} }$

Является ли монотонной данная разностная схема? $(1 + \frac{1}{{2\varepsilon }}\sum\limits_j {{\alpha _{{k_j}}}} X_j^2)U_k^{n + 1} = (\frac{1}{{2\varepsilon }}\sum\limits_j {X_j^2{\alpha _{{k_j}}})U_k^n + } \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} }$

Укажите условия аппроксимации разностных схем с порядком $O({\tau ^2},{h^4})$ , исходя из дифференциального приближения к исходному уравнению параболического типа: ${\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots$

Укажите условия аппроксимации разностных схем с порядком $O(\tau ,{h^2})$ , исходя из дифференциального приближения к исходному уравнению параболического типа: ${\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots$

Используя обозначения из лекций, укажите уравнения, не являющиеся условиями аппроксимации первого порядка разностных схем для данного эллиптического уравнения: ${u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})$

Используя обозначения из лекций, укажите уравнения, не являющиеся условиями аппроксимации второго порядка разностных схем для данного эллиптического уравнения: ${u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})$

Приведенная ниже система уравнений, является системой уравнений: ${u_t} + {\lambda _i}{u_{ix}} = {\varepsilon _i}{u_{ixx}}$

Возможно ли построение монотонной по Фридрихсу разностной схемы для эллиптического уравнения ${u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})$ на произвольном наборе сеточных узлов?

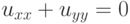Возможно ли построение монотонной по Фридрихсу разностной схемы для эллиптического уравнения $\[{u_{xx}} + {u_{yy}} = 0$ на произвольном наборе сеточных узлов?

Используя обозначения из лекций, укажите условия аппроксимации второго порядка разностных схем для данного эллиптического уравнения: ${u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})$