Нелинейные вычислительные процессы - ответы
Количество вопросов - 180
Укажите условия, при которых разностная схема для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) монотонна по Годунову при
монотонна по Годунову при ![\[{u_x}{u_{xx}} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/57f3634c686df163a321e0b0fb896fa8.png)
Определите верную запись критерия устойчивости разностных схем для уравнений параболического типа:
Какая формальная запись соответствует обобщению одномерных скалярных разностных схем в случае линейной параболической системы уравнений?
Если разностная схема не удовлетворяет тем же интегральным соотношениям, что и первоначальное дифференциальное уравнение, то данная схема:
При выполнении какого условия, данное уравнение будет эллиптическим? ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
Если в дифференциальном приближении к исходному уравнению параболического типа ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 0,{\rm{ }}{\delta _1} = 0,{\rm{ }}{\delta _2} = 1\]](https://intuit.ru//sites/default/files/tex_cache/4c2b30d247b46f690c34fbcb7897ab7a.png) , то:
, то:
Укажите порядок данного дифференциального уравнения: ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
Определите условие параболичности для данного уравнения: ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png)
Используя обозначения из лекций, укажите условия аппроксимации первого порядка разностных схем для данного эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Назовите порядок аппроксимации разностной схемы Лакса-Вендроффа:
Укажите квазилинейную форму записи одномерных уравнений Эйлера:
Для дивергентной системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо:
справедливо:
Определите, чем является приведенное ниже выражение: ![\[{\alpha _1}({{\vec U}_t} + \frac{1}{{{\alpha _1}}}{{\vec F}_{1x}}) + {\alpha _2}({{\vec U}_t} + \frac{1}{{{\alpha _2}}}{{\vec F}_{2y}}) + {\alpha _3}({{\vec U}_t} + \frac{1}{{{\alpha _3}}}{{\vec F}_{3z}}) = 0\]](https://intuit.ru//sites/default/files/tex_cache/c021df03a648e7e5d0317324c802376e.png)
Укажите запись системы уравнений Бюргерса:
Укажите, чем является приведенное ниже уравнение: ![\[h(\vec U_m^{n + 1/2} - \vec U_m^{n - 1/2}) - [(B{{\vec U}_x})_{m + 1/2}^n - (B{{\vec U}_x})_{m - 1/2}^n]\tau = 0\]](https://intuit.ru//sites/default/files/tex_cache/fd7ec43afb90539c1542631d5bcce039.png)
Определите, чем является приведенное ниже выражение: ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png)
Укажите дивергентную форму записи одномерных уравнений Эйлера:
Укажите разностную схему Лакса-Вендроффа:
При каком условии, приведенная ниже система уравнений, может являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Укажите разностную схему "крест":
Какой метод регуляризации разностных схем подразумевает использование в схеме малого положительного коэффициента \varepsilon?
Возможно ли построение монотонной по Фридрихсу разностной схемы для эллиптического уравнения 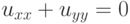 на произвольном наборе сеточных узлов?
на произвольном наборе сеточных узлов?
Является ли явной данная разностная схема? ![\[(1 + \frac{1}{{2\varepsilon }}\sum\limits_j {{\alpha _{{k_j}}}} X_j^2)U_k^{n + 1} = (\frac{1}{{2\varepsilon }}\sum\limits_j {X_j^2{\alpha _{{k_j}}})U_k^n + } \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} } \]](https://intuit.ru//sites/default/files/tex_cache/9403491e41297a94ceb0493f4403cc70.png)
Используя обозначения из лекций, определите название для данной формы записи: ![\[{\vec S_t} + {({\vec F_{\vec \upsilon }}\vec W_{\vec \upsilon }^{ - 1}\vec S)_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/df0f632b300b4e523fe1f0b5e9903ab9.png)
Используя обозначения из лекций, укажите уравнения, не являющиеся условиями аппроксимации второго порядка разностных схем для данного эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Разностная схема Лакса-Вендроффа всегда ...
Укажите название записанных ниже краевых условий для уравнений параболического типа: ![\[u(t,0) = {u^1}(t),{\rm{ }}\frac{{\partial u}}{{\partial x}}(t,1) = {u^4}(t)\]](https://intuit.ru//sites/default/files/tex_cache/741667794c2197c28fadfb01910f4bf6.png)
Выберите уравнение, являющееся критерием устойчивости разностных схем для уравнений параболического типа:
Укажите условия аппроксимации разностных схем с порядком ![\[O({\tau ^2},{h^4})\]](https://intuit.ru//sites/default/files/tex_cache/4abea93ed37cffe5eb5fdb915df35c9d.png) , исходя из дифференциального приближения к исходному уравнению параболического типа:
, исходя из дифференциального приближения к исходному уравнению параболического типа: ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png)
Определите название следующей разностной схемы: ![\[\frac{{\upsilon _m^{n + 1} - \upsilon _m^n}}{\tau } + \lambda \frac{{\upsilon _m^n - \upsilon _{m - 1}^n}}{h} = 0\]](https://intuit.ru//sites/default/files/tex_cache/07f7a72d716e107c1e6bdac08e66bcb1.png)
Укажите, какой является данная система уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Систему квазилинейных уравнений, в которой коэффициенты перед частными производными не зависят от искомых функций, называют:
Укажите порядок данной системы уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t)\]](https://intuit.ru//sites/default/files/tex_cache/65c17bfe29ff9cd39848e6ce53844d9c.png)
При каких условиях, приведенная ниже система уравнений, не будет являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Укажите запись расширенной системы гиперболических уравнений в дивергентной форме:
Укажите название формы записи гиперболического уравнения: ![\[\frac{{\partial {U_i}}}{{\partial t}} + {\lambda _i}\frac{{\partial {U_i}}}{{\partial x}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/5c78367003e5c4cc58d4be8b778058c5.png)
Укажите название формы записи системы гиперболических уравнений: ![\[\frac{{\partial \overrightarrow W (\overrightarrow \upsilon ,t,x)}}{{\partial t}} + \frac{{\partial \overrightarrow F (\overrightarrow \upsilon ,t,x)}}{{\partial x}} = \overrightarrow P \]](https://intuit.ru//sites/default/files/tex_cache/96d202cca2f59fb7fff8de7775b2ec81.png)
Укажите название формы записи системы гиперболических уравнений: ![\[\Omega \frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + \Lambda \Omega \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \Omega \overrightarrow f \]](https://intuit.ru//sites/default/files/tex_cache/a417aa0c9a321b2bb043c2800dc0a5ee.png)
Укажите, исходя из приведенного ниже соотношения, обозначение инвариант Римана: ![\[\overrightarrow U = \Omega \overrightarrow \upsilon \]](https://intuit.ru//sites/default/files/tex_cache/c619e9d8a9abdf9657b5957cb7b6bdf4.png)
При выполнении какого условия, данное уравнение будет гиперболическим? ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
При выполнении условия ![\[{B^2} - AC < 0\]](https://intuit.ru//sites/default/files/tex_cache/c167c84366913d4545ab3cd37302d8b0.png) , приведенное ниже уравнение будет:
, приведенное ниже уравнение будет: ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
Укажите разностную схему Куранта-Изаксона-Риса:
Какая разностная схема состоит из предиктора и корректора?
Укажите разностную схему Ландау-Меймана-Халатникова:
Для метода регуляризации разностных схем с помощью введения искусственной вязкости:
Для метода регуляризации разностных схем с помощью метода сглаживания численного решения:
К каким разностным схемам относятся схемы, для которых справедливо: ![\[\alpha _\mu ^\nu = \alpha _\mu ^\nu (\tau ,h,\upsilon _r^p)\]](https://intuit.ru//sites/default/files/tex_cache/9c5042f6085a8d1d3513124670e1e3b1.png)
Назовите порядок аппроксимации разностной схемы Ландау-Меймана-Халатникова:
Укажите условие для монотонных нелинейных разностных схем по Хартену:
Укажите условие для монотонных нелинейных разностных схем по Ван Лиру:
Разностная схема Лакса-Вендроффа является:
Для линейной системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо:
справедливо:
Определите, чем является приведенное ниже выражение: ![\[\frac{d}{{dt}}\int {\int\limits_G {\int {\vec UdG} } } + \oint\limits_S {\vec Fd\vec S = 0} \]](https://intuit.ru//sites/default/files/tex_cache/749c6c8ef2a476de6299512e8efe5f3e.png)
Укажите условия, при которых разностная схема для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) не монотонна по Годунову при
не монотонна по Годунову при ![\[{u_x}{u_{xx}} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/57f3634c686df163a321e0b0fb896fa8.png)
Укажите выражение разностной аппроксимации интегрального тождества для многомерных гиперболических систем уравнений в случае неструктурированных сеток:
Для нелинейной системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо:
справедливо:
Укажите выражение многомерной гиперболической системы уравнений:
Выражение ![\[F_{k,k - 1}^j = \frac{1}{2}({F_k} + {F_{k - 1}}) + \frac{1}{2}(\Omega _L^{ - 1}\left| \Lambda \right|{\Omega _L})({{\vec U}_k} - {{\vec U}_{k - 1}})\]](https://intuit.ru//sites/default/files/tex_cache/1e3e155a2eda08c41fd60838de3824e1.png) является формой записи:
является формой записи:
Укажите выражение разностной схемы для продолженной системы гиперболических уравнений на явном трехточечном шаблоне:
Укажите условия, при которых разностная схема для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) монотонна по Годунову при
монотонна по Годунову при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png)
Для уравнения переноса определения монотонности по Ван-Лиру и по Годунову в общей области их действия:
В случае, когда для системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо
справедливо ![\[{{\vec U}_t} + {{\vec F}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/84996a4af0ed7dd649a67bbb226c1b42.png) ,
, ![\[A = \frac{{\partial \vec F}}{{\partial \vec U}}\]](https://intuit.ru//sites/default/files/tex_cache/77d534b64eae3af2323604698f01fa3e.png) , то данная система является:
, то данная система является:
Укажите выражение метода расщепления по пространственным переменным для многомерных систем гиперболических уравнений:
Укажите условия параболичности для системы уравнений: ![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
Уравнение Бюргерса является ...
Укажите название записанных ниже краевых условий для уравнений параболического типа: ![\[u(t,0) = {u^1}(t),{\rm{ }}u(t,1) = {u^2}(t)\]](https://intuit.ru//sites/default/files/tex_cache/1a57fd79a45c88163dd874b687339695.png)
Какая из форм записи краевых условий для уравнений параболического типа соответствует задаче Неймана
Решение параболических уравнений...
Задача поиска монотонных по Фридрихсу схем первого порядка аппроксимации по времени ...
Укажите, чем является приведенное ниже уравнение: ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png)
Укажите, чем является приведенное ниже уравнение: ![\[\int\limits_{{t^{n - 1/2}}}^{{t^{n + 1/2}}} {dt\int\limits_{{x_{m - 1/2}}}^{{x_{m + 1/2}}} {dx} } ({{\vec U}_t} - {(B{{\vec U}_x})_x}) = 0\]](https://intuit.ru//sites/default/files/tex_cache/4cacc7a22d574ae8ac9b6454cdd12e61.png)
Выберите уравнение, являющееся дифференциальным приближением к исходному уравнению параболического типа:
Если в дифференциальном приближении к исходному уравнению параболического типа ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 0,{\rm{ }}{\delta _1} = 0,{\rm{ }}{\delta _2} = 0\]](https://intuit.ru//sites/default/files/tex_cache/a2752d479db9a49153b1fd941efd0353.png) , то:
, то:
Используя обозначения из лекций, укажите уравнения, не являющиеся условиями аппроксимации первого порядка разностных схем для данного эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Используя обозначения из лекций, укажите условия аппроксимации второго порядка разностных схем для данного эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Укажите среди перечисленных, уравнение эллиптического типа:
Приведенная ниже запись уравнения соответствует: ![\[{u_{xx}} + {u_{yy}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/95a55fa134e876a66a1fb359c90c59aa.png)
Определите условие эллиптичности для данного уравнения: ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png)
Для того, чтобы было возможно построение монотонной по Фридрихсу разностной схемы первого порядка аппроксимации для эллиптического уравнения на произвольном наборе сеточных узлов, необходимо:
Укажите разностную схему при произвольном временном шаге интегрирования для данного уравнения: ![\[{u_t} = {\varepsilon _1}{u_{xx}} + {\varepsilon _2}{u_{yy}}\]](https://intuit.ru//sites/default/files/tex_cache/c40106c67a9fa1b652be7013e6e31ff0.png)
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{X_j}{Y_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/19426c9d421edb450c399cf7c476a422.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Название итерационного метода: ![\[U_k^{n + 1} = \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1}} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} \]](https://intuit.ru//sites/default/files/tex_cache/745815c83ada1cd5375f53b2d59ab093.png)
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{X_j}({Y_j}^2 - {{\frac{{{X_j}}}{3}}^2})} {\alpha _{{k_j}}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/c98bb9791942b7268f311af37c5170c9.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{X_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/e78d96387930883d8656a9562807fc06.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Определите условие гиперболичности для данного уравнения: ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png)
Если в разностной схеме для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) при
при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png) будут выполняться условия
будут выполняться условия ![\[\alpha _{ - 1}^0,\alpha _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/1c5f76cbec0672c76b093481e505fc39.png) ,
, ![\[\beta _{ - 1}^0,\beta _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/f2cb98339ae8bdd5dad161571abbac37.png) , то данная схема:
, то данная схема:
Укажите, какая из перечисленных ниже форм записи гиперболических уравнений, является дивергентной системой гиперболических уравнений:
При каком условии, приведенная ниже система уравнений, не может являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Укажите, в каком случае можно систему уравнений ![\[{(A{{\vec \upsilon }_x})_x} + {(B{{\vec \upsilon }_y})_y} + {(C{{\vec \upsilon }_x})_y} + {(D{{\vec \upsilon }_y})_x} = \vec f\]](https://intuit.ru//sites/default/files/tex_cache/82f667e68484770531a51aaab6728337.png) привести к виду
привести к виду ![\[{\Lambda _1}{{\vec U}_{xx}} + ({\Lambda _3} + {\Lambda _4}){{\vec U}_{xy}} + {\Lambda _2}{{\vec U}_{yy}} = \Omega \vec f\]](https://intuit.ru//sites/default/files/tex_cache/b70e760335009f02b0c75496979cea23.png)
В случае если для уравнения ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png) , выражение
, выражение ![\[{({\lambda _3} + {\lambda _4})^2} - 4{\lambda _1}{\lambda _2} = 0\]](https://intuit.ru//sites/default/files/tex_cache/71a76b4034ddc1d0ecfea0a7f77059df.png) , данное уравнение:
, данное уравнение:
Разностная схема Ландау-Меймана-Халатникова является:
Укажите условия аппроксимации разностных схем с порядком ![\[O(\tau ,{h^2})\]](https://intuit.ru//sites/default/files/tex_cache/a8d190488e2325f97e622ec7199c4847.png) , исходя из дифференциального приближения к исходному уравнению параболического типа:
, исходя из дифференциального приближения к исходному уравнению параболического типа: ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png)
Число Куранта определяется как:
Возможно ли построение монотонной по Фридрихсу разностной схемы для эллиптического уравнения ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png) на произвольном наборе сеточных узлов?
на произвольном наборе сеточных узлов?
Укажите, чем является приведенное ниже уравнение: ![\[\vec U_m^{n + 1} = \sum\limits_{\mu ,\nu } {{\Omega ^{ - 1}}} A_\mu ^\nu \Omega \vec U_{m + \mu }^{n + \nu }\]](https://intuit.ru//sites/default/files/tex_cache/0d8e242adb0a272f631cfdc59d50bd07.png)
Приведенная ниже система уравнений, является системой уравнений: ![\[{u_t} + {\lambda _i}{u_{ix}} = {\varepsilon _i}{u_{ixx}}\]](https://intuit.ru//sites/default/files/tex_cache/dc48dbf6ac4ecd07b9d04112cc94e4d0.png)
Укажите название формы записи гиперболического уравнения: ![\[{\overrightarrow \omega _i}\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + {\lambda _i}{\overrightarrow \omega _i}\frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = {\overrightarrow \omega _i}\overrightarrow f \]](https://intuit.ru//sites/default/files/tex_cache/60faa1e284da9184ef447b42af330f71.png)
Укажите разностную схему Лакса:
Компоненты какого вектора из приведенного ниже соотношения, являются инвариантами Римана? ![\[\overrightarrow U = \Omega \overrightarrow \upsilon \]](https://intuit.ru//sites/default/files/tex_cache/c619e9d8a9abdf9657b5957cb7b6bdf4.png)
Коэффициенты в сеточных узлах симметричных схем для параболического уравнения удовлетворяют равенству:
Для того, чтобы было возможно построение монотонной по Фридрихсу разностной схемы второго порядка аппроксимации для эллиптического уравнения на произвольном наборе сеточных узлов, необходимо:
При каких значениях числа Куранта предпочтительно использование явных разностных схем?
Разностная схема Ландау-Меймана-Халатникова всегда ...
Монотонные разностные схемы по Фридрихсу могут иметь:
Для метода регуляризации разностных схем с помощью метода по Фридрихсу:
Укажите выражение интегрального тождества для многомерных гиперболических систем уравнений в случае неструктурированных сеток:
Укажите, какой является данная система уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t)\]](https://intuit.ru//sites/default/files/tex_cache/65c17bfe29ff9cd39848e6ce53844d9c.png)
Критерием какой монотонной нелинейной разностной схемы является выполнение следующего условия: ![\[\min \{ u_1^n,u_2^n\} \le u_m^{n + 1} \le \max \{ u_1^n,u_2^n\} \]](https://intuit.ru//sites/default/files/tex_cache/dc81d35b75367b97d1e26d3afa471f50.png)
В случае, когда для системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо
справедливо ![\[A = \{ {a_{ij}}\} \]](https://intuit.ru//sites/default/files/tex_cache/a0f4a77604e9bb80fe70ed920a283371.png) ,
, ![\[{i_{ij}} = \overline {1,I} \]](https://intuit.ru//sites/default/files/tex_cache/29da55d640bccf34e8f3a5301382d7c8.png) ,
, ![\[{a_{ij}} = const\]](https://intuit.ru//sites/default/files/tex_cache/39f7f8036bf0866716cee4dd09d4189a.png) , то данная система является:
, то данная система является:
Если в разностной схеме для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) при
при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png) будут выполняться условия
будут выполняться условия ![\[\alpha _{ - 1}^0,\alpha _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/1c5f76cbec0672c76b093481e505fc39.png) ,
, ![\[\beta _{ - 1}^0,\beta _0^0 \le 0\]](https://intuit.ru//sites/default/files/tex_cache/a4bc95a8b8cdf9326fa729812c3b86fc.png) , то данная схема:
, то данная схема:
Какая формальная запись соответствует разностной аппроксимации интегрального тождества дивергентной формы систем уравнений параболического типа?
В случае, когда для системы гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) справедливо
справедливо ![\[A = A(t,x,\vec U)\]](https://intuit.ru//sites/default/files/tex_cache/f3cb79b13e87f0d03e977fa808d80f77.png) , то данная система является:
, то данная система является:
Критерием какой монотонной нелинейной разностной схемы является выполнение следующего условия: ![\[TV(u_m^{n + 1}) \le TV(u_m^n)\]](https://intuit.ru//sites/default/files/tex_cache/fd067cf533b89ca639f22575b46d5fd7.png)
Равенство коэффициентов ![\[\alpha _{ - \mu }^\nu = \alpha _\mu ^\nu \]](https://intuit.ru//sites/default/files/tex_cache/f00fd0409cfda411b8a2fb068ded1b1b.png) в сеточных узлах разностных схем для параболического уравнения характерно для:
в сеточных узлах разностных схем для параболического уравнения характерно для:
Определите, чем является приведенное ниже выражение: ![\[\frac{{U_m^{n + 1} - U_m^n}}{\tau } + \frac{{F_{m + 1/2}^{n + 1/2} - F_{m - 1/2}^{n + 1/2}}}{h} = 0\]](https://intuit.ru//sites/default/files/tex_cache/e9cbf0e21b7969e8f42dc490455d4762.png)
Сколько условий аппроксимации разностных схем эллиптических уравнений существует в общем случае для первого порядка аппроксимации?
Укажите условие, при котором приведенная ниже система уравнений, может являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Укажите порядок данной системы уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
Укажите, какая из перечисленных ниже форм записи гиперболических уравнений, является условием совместности вдоль характеристических направлений:
Укажите, какое из уравнений не является одномерными уравнениями Эйлера:
При выполнении условия ![\[{B^2} - AC > 0\]](https://intuit.ru//sites/default/files/tex_cache/a09d1686f6fb620c5938d8f7155b5558.png) , приведенное ниже уравнение будет:
, приведенное ниже уравнение будет: ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
Определите название следующей разностной схемы: ![\[\frac{{\upsilon _m^{n + 1} - 0,5(\upsilon _{m - 1}^n + \upsilon _{m + 1}^n)}}{\tau } + \frac{{\lambda (\upsilon _{m + 1}^n - \upsilon _{m - 1}^n)}}{{2h}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/c8d7996dc8ce443298bbe400dc9324c5.png)
Назовите порядок аппроксимации разностной схемы "крест":
Определите название следующей разностной схемы: ![\[\frac{{\upsilon _m^{n + 1} - \upsilon _m^n}}{\tau } + \lambda \frac{{\upsilon _{m + 1/2}^{n + 1/2} - \upsilon _{m - 1/2}^{n + 1/2}}}{h} = 0\]](https://intuit.ru//sites/default/files/tex_cache/8ddab879e5e3e9eada6036ae5a73ee0c.png)
К каким разностным схемам относятся схемы, для которых справедливо: ![\[\alpha _\mu ^\nu = \alpha _\mu ^\nu (\tau ,h)\]](https://intuit.ru//sites/default/files/tex_cache/be582f4c03f60f0a761673b254616f9c.png)
Какой метод регуляризации разностных схем использует следующую формулу: ![\[\upsilon _m^{n + 1} = \varphi \cdot \tilde \upsilon _{m - 1}^{n + 1} + (1 - 2\varphi )\tilde \upsilon _m^{n + 1} + \varphi \cdot \tilde \upsilon _{m + 1}^{n + 1}\]](https://intuit.ru//sites/default/files/tex_cache/f55c0ebf2a5f14b0511e854e8e35cb15.png)
Какой метод регуляризации разностных схем требует, чтобы выполнялось условие: ![\[\alpha _\mu ^\nu \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/ab7583ec715c0875a4e41f1e2637961f.png)
Критерием какой монотонной нелинейной разностной схемы является выполнение следующего условия: ![\[u_{m + 1}^{n + 1} - u_m^{n + 1} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/3fd819cc77c34e7a81712fbd5a6df97f.png) , если
, если ![\[u_{m + 1}^n - u_m^n \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/c555704040f29819b0b78bfd0c355c7e.png)
Неявные разностные схемы ...
Когда разностная схема удовлетворяет тем же интегральным соотношениям, что и первоначальное дифференциальное уравнение, то говорят о свойстве:
Используя обозначения из лекций, укажите выражение интерполяционного многочлена, обеспечивающего вычисление потоков на гранях ячеек Дирихле:
Для уравнения переноса определения монотонности по Ван-Лиру и по Фридрихсу в общей области их действия:
Укажите условие, при котором приведенная ниже система уравнений, может являться системой параболического типа? ![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
Укажите критерий устойчивости разностных схем для уравнений параболического типа:
Какая формальная запись соответствует интегральному тождеству для дивергентной формы систем уравнений параболического типа?
Укажите, чем является приведенное ниже уравнение: ![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
Если в дифференциальном приближении к исходному уравнению параболического типа ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 1,{\rm{ }}{\delta _1} = 1,{\rm{ }}{\delta _2} = 0\]](https://intuit.ru//sites/default/files/tex_cache/2c9a10d6d2832b51cfd1f87ca139af60.png) , то:
, то:
Решение эллиптических уравнений...
Укажите уравнение Лапласа:
В случае если для уравнения ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png) , выражение
, выражение ![\[{({\lambda _3} + {\lambda _4})^2} - 4{\lambda _1}{\lambda _2} < 0\]](https://intuit.ru//sites/default/files/tex_cache/3fe21c1d3602de92a7fbd79d5fa223d0.png) , данное уравнение является:
, данное уравнение является:
Если в системе уравнений ![\[{(A{{\vec \upsilon }_x})_x} + {(B{{\vec \upsilon }_y})_y} + {(C{{\vec \upsilon }_x})_y} + {(D{{\vec \upsilon }_y})_x} = \vec f\]](https://intuit.ru//sites/default/files/tex_cache/82f667e68484770531a51aaab6728337.png) все матрицы попарно коммутируют между собой, то:
все матрицы попарно коммутируют между собой, то:
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{Y_j}({Y_j}^2 - 3{X_j}^2)} {\alpha _{{k_j}}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/e7c8aabbf59f5c5f801917fdd9428f5d.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Сколько условий аппроксимации разностных схем эллиптических уравнений существует в общем случае для второго порядка аппроксимации?
Укажите, чем является приведенное ниже уравнение: ![\[\left| q \right| = \sum\limits_{\mu ,\nu } {\alpha _\mu ^\nu } {q^\nu }{e^{imkh}}\]](https://intuit.ru//sites/default/files/tex_cache/ca06f8fc704565b6fa270c2265d5acda.png)
При каком условии, приведенная ниже система уравнений, может являться системой параболического типа? ![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
Укажите название для следующего выражения:
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{Y_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/8d48499ef029d22b39a70ebac8c48cf3.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {{\alpha _{{k_j}}}} = 1\]](https://intuit.ru//sites/default/files/tex_cache/c30b4d5a1b88ee56ed99c80363c9a1cc.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Укажите условие для монотонных нелинейных разностных схем по Годунову:
Определите название следующей разностной схемы: ![\[\frac{{\upsilon _m^{n + 1} - \upsilon _m^{n - 1}}}{{2\tau }} + \lambda \frac{{\upsilon _{m + 1}^n - \upsilon _{m - 1}^n}}{{2h}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/d80bb601c86b6cebe9f2e077a2e5c6af.png)
Укажите условия, при которых разностная схема для продолженной системы гиперболических уравнений на явном трехточечном шаблоне ![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) не монотонна по Годунову при
не монотонна по Годунову при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png)
Укажите выражение разностной схемы, получаемой из интегральной формы системы гиперболических уравнений: ![\[{{\vec U}_t} + {{\vec F}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/84996a4af0ed7dd649a67bbb226c1b42.png)
Укажите, какая из перечисленных ниже форм записи гиперболических уравнений, является квазилинейной системой гиперболических уравнений:
Используя обозначения из лекций, укажите условие аппроксимации второго порядка разностных схем для эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Укажите, какой является данная система уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/21b52146d2b14dd7f5e410fc83a3ab7d.png)
При каких условиях, приведенная ниже система уравнений, будет являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
При выполнении какого условия, данное уравнение будет параболическим? ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
При каких значениях числа Куранта предпочтительно использование неявных разностных схем?
Определите, чем является приведенное ниже выражение: ![\[{{\vec U}_t} + {{\vec F}_{1x}} + {{\vec F}_{2y}} + {{\vec F}_{3z}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/b742237cadaa5e939b01b639a8ca6ab6.png)
Укажите название записанных ниже краевых условий для уравнений параболического типа: ![\[\frac{{\partial u}}{{\partial x}}(t,0) = {u^3}(t),{\rm{ }}\frac{{\partial u}}{{\partial x}}(t,1) = {u^4}(t)\]](https://intuit.ru//sites/default/files/tex_cache/013e450b269f567d978fd3a98fc0f6fa.png)
Какая из форм записи краевых условий для уравнений параболического типа соответствует смешанной задаче?
Уравнение Лапласа является уравнением ...
Является ли монотонной данная разностная схема? ![\[(1 + \frac{1}{{2\varepsilon }}\sum\limits_j {{\alpha _{{k_j}}}} X_j^2)U_k^{n + 1} = (\frac{1}{{2\varepsilon }}\sum\limits_j {X_j^2{\alpha _{{k_j}}})U_k^n + } \sum\limits_{j < k} {{\alpha _{{k_j}}}U_j^{n + 1} + \sum\limits_{j > k} {{\alpha _{{k_j}}}U_j^n} } \]](https://intuit.ru//sites/default/files/tex_cache/9403491e41297a94ceb0493f4403cc70.png)
Используя обозначения из лекций, укажите условие аппроксимации первого порядка разностных схем для эллиптического уравнения: ![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
Укажите порядок данной системы уравнений: ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/21b52146d2b14dd7f5e410fc83a3ab7d.png)
Систему квазилинейных уравнений, в которой коэффициенты перед частными производными зависят от искомых функций, называют:
Система гиперболических уравнений ![\[{{\vec U}_t} + A{{\vec U}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/014a77a79f161c9774934746c718c3cf.png) , являющаяся квазилинейной ...
, являющаяся квазилинейной ...
Выберите уравнение, являющееся системой дифференциальных уравнений параболического типа:
Назовите порядок аппроксимации разностной схемы Куранта-Изаксона-Риса:
Определите название следующей разностной схемы: ![\[\frac{{\upsilon _m^{n + 1} - \upsilon _m^n}}{\tau } + \frac{{\lambda (\upsilon _m^{n + 1} - \upsilon _{m - 1}^{n + 1})}}{h} = 0\]](https://intuit.ru//sites/default/files/tex_cache/deb0d7fc1d90391f5ff5fbfbc143e5f9.png)
В методе Годунова по вычислению потоков на гранях ячеек Дирихле используется:
Условие аппроксимации разностных схем эллиптических уравнений ![\[\sum\limits_j {({Y_j}^2 - {X_j}^2){\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/d112058281e26ba295503e3697779e7a.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:
Явные разностные схемы ...
Определите, чем является приведенное ниже выражение: ![\[{G_k}\frac{{U_k^{n + 1} - U_k^n}}{\tau } + \sum\limits_{j = 1}^{{J_k}} {({{\vec F}_{{k_j}}}{{\vec S}_j}} ) = 0\]](https://intuit.ru//sites/default/files/tex_cache/6f971da70139cfdf59eb055247f547d8.png)
Определите условия, при которых приведенное ниже уравнение не будет являться эллиптическим: ![\[{\lambda _1}{u_{xx}} + ({\lambda _3} + {\lambda _4}){u_{xy}} + {\lambda _2}{u_{yy}} = \varphi \]](https://intuit.ru//sites/default/files/tex_cache/d27d265ecce7606cd542dc509a5d307a.png)
Укажите, какая из перечисленных ниже форм записи гиперболических уравнений, является скалярным уравнением переноса:
Укажите условие, при котором приведенная ниже система уравнений, не может являться системой гиперболического типа? ![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
При выполнении условия ![\[{B^2} - AC = 0\]](https://intuit.ru//sites/default/files/tex_cache/ab21bc6140b1d7db5bc86d7e604966ba.png) , приведенное ниже уравнение будет:
, приведенное ниже уравнение будет: ![\[L(u) = A\frac{{{\partial ^2}u}}{{\partial {x^2}}} + 2B\frac{{{\partial ^2}u}}{{\partial x\partial t}} + C\frac{{{\partial ^2}u}}{{\partial {t^2}}} + D\frac{{\partial u}}{{\partial x}} + E\frac{{\partial u}}{{\partial t}} + Gu(x,t) = 0\]](https://intuit.ru//sites/default/files/tex_cache/8aa941a133ee1d70376b56903cdfc597.png)
Задача поиска монотонных по Фридрихсу схем второго порядка аппроксимации по времени ...
Какая из форм записи краевых условий для уравнений параболического типа соответствует задаче Дирихле?

![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) монотонна по Годунову при
монотонна по Годунову при ![\[{u_x}{u_{xx}} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/57f3634c686df163a321e0b0fb896fa8.png)
![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 0,{\rm{ }}{\delta _1} = 0,{\rm{ }}{\delta _2} = 1\]](https://intuit.ru//sites/default/files/tex_cache/4c2b30d247b46f690c34fbcb7897ab7a.png) , то:
, то:![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
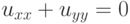 на произвольном наборе сеточных узлов?
на произвольном наборе сеточных узлов?![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[O({\tau ^2},{h^4})\]](https://intuit.ru//sites/default/files/tex_cache/4abea93ed37cffe5eb5fdb915df35c9d.png) , исходя из дифференциального приближения к исходному уравнению параболического типа:
, исходя из дифференциального приближения к исходному уравнению параболического типа: ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png)
![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) не монотонна по Годунову при
не монотонна по Годунову при ![\[{u_x}{u_{xx}} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/57f3634c686df163a321e0b0fb896fa8.png)
![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) монотонна по Годунову при
монотонна по Годунову при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png)
![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 0,{\rm{ }}{\delta _1} = 0,{\rm{ }}{\delta _2} = 0\]](https://intuit.ru//sites/default/files/tex_cache/a2752d479db9a49153b1fd941efd0353.png) , то:
, то:![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[\sum\limits_j {{X_j}{Y_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/19426c9d421edb450c399cf7c476a422.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[\sum\limits_j {{X_j}({Y_j}^2 - {{\frac{{{X_j}}}{3}}^2})} {\alpha _{{k_j}}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/c98bb9791942b7268f311af37c5170c9.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[\sum\limits_j {{X_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/e78d96387930883d8656a9562807fc06.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) при
при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png) будут выполняться условия
будут выполняться условия ![\[\alpha _{ - 1}^0,\alpha _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/1c5f76cbec0672c76b093481e505fc39.png) ,
, ![\[\beta _{ - 1}^0,\beta _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/f2cb98339ae8bdd5dad161571abbac37.png) , то данная схема:
, то данная схема:![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
![\[O(\tau ,{h^2})\]](https://intuit.ru//sites/default/files/tex_cache/a8d190488e2325f97e622ec7199c4847.png) , исходя из дифференциального приближения к исходному уравнению параболического типа:
, исходя из дифференциального приближения к исходному уравнению параболического типа: ![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png)
![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png) на произвольном наборе сеточных узлов?
на произвольном наборе сеточных узлов?![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) при
при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png) будут выполняться условия
будут выполняться условия ![\[\alpha _{ - 1}^0,\alpha _0^0 \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/1c5f76cbec0672c76b093481e505fc39.png) ,
, ![\[\beta _{ - 1}^0,\beta _0^0 \le 0\]](https://intuit.ru//sites/default/files/tex_cache/a4bc95a8b8cdf9326fa729812c3b86fc.png) , то данная схема:
, то данная схема:![\[\alpha _{ - \mu }^\nu = \alpha _\mu ^\nu \]](https://intuit.ru//sites/default/files/tex_cache/f00fd0409cfda411b8a2fb068ded1b1b.png) в сеточных узлах разностных схем для параболического уравнения характерно для:
в сеточных узлах разностных схем для параболического уравнения характерно для:![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
![\[u_{m + 1}^{n + 1} - u_m^{n + 1} \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/3fd819cc77c34e7a81712fbd5a6df97f.png) , если
, если ![\[u_{m + 1}^n - u_m^n \ge 0\]](https://intuit.ru//sites/default/files/tex_cache/c555704040f29819b0b78bfd0c355c7e.png)
![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
![\[{\upsilon _t} - \varepsilon {\upsilon _{xx}} = \frac{{{\delta _0}}}{\tau }\upsilon + \frac{{{\delta _1}{h^2}}}{{2\tau }}{\upsilon _{xx}} + \frac{{{\delta _2}{h^4}}}{{4\tau }}{\upsilon _{xxxx}} + \ldots \]](https://intuit.ru//sites/default/files/tex_cache/5eb3d5f41dc1bed146b63a51fcf5b655.png) значение коэффициентов равно
значение коэффициентов равно ![\[{\delta _0} = 1,{\rm{ }}{\delta _1} = 1,{\rm{ }}{\delta _2} = 0\]](https://intuit.ru//sites/default/files/tex_cache/2c9a10d6d2832b51cfd1f87ca139af60.png) , то:
, то:![\[\sum\limits_j {{Y_j}({Y_j}^2 - 3{X_j}^2)} {\alpha _{{k_j}}} = 0\]](https://intuit.ru//sites/default/files/tex_cache/e7c8aabbf59f5c5f801917fdd9428f5d.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[{\vec \upsilon _t} - {\vec F_x} = {(B(t,x,\vec \upsilon ){\vec \upsilon _x})_x}\]](https://intuit.ru//sites/default/files/tex_cache/cac3daa23437dd9580d8830d2edf05af.png)
![\[\sum\limits_j {{Y_j}{\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/8d48499ef029d22b39a70ebac8c48cf3.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[\sum\limits_j {{\alpha _{{k_j}}}} = 1\]](https://intuit.ru//sites/default/files/tex_cache/c30b4d5a1b88ee56ed99c80363c9a1cc.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[u_m^{n + 1} = \alpha _{ - 1}^0u_{m - 1}^n + \alpha _0^0u_m^n + \beta _{ - 1}^0h\upsilon _{m - 1}^n + \beta _0^0h\upsilon _m^n\]](https://intuit.ru//sites/default/files/tex_cache/4b4b6ec6f75a703444dd3a66e7b8394c.png) не монотонна по Годунову при
не монотонна по Годунову при ![\[{u_x}{u_{xx}} \le 0\]](https://intuit.ru//sites/default/files/tex_cache/057bd6176bc8554c247324e1ea63560b.png)
![\[{{\vec U}_t} + {{\vec F}_x} = 0\]](https://intuit.ru//sites/default/files/tex_cache/84996a4af0ed7dd649a67bbb226c1b42.png)
![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)
![\[{u_{xx}} + {u_{yy}} = f(x,y,u,{u_x},{u_y})\]](https://intuit.ru//sites/default/files/tex_cache/20c664d667815dc141f84ae9de9d3f02.png)
![\[\sum\limits_j {({Y_j}^2 - {X_j}^2){\alpha _{{k_j}}} = 0} \]](https://intuit.ru//sites/default/files/tex_cache/d112058281e26ba295503e3697779e7a.png) (используются обозначения из лекций), является условием аппроксимации:
(используются обозначения из лекций), является условием аппроксимации:![\[\frac{{\partial \overrightarrow \upsilon }}{{\partial t}} + A(x,t,\overrightarrow \upsilon ) \cdot \frac{{\partial \overrightarrow \upsilon }}{{\partial x}} = \overrightarrow f (x,t,\overrightarrow \upsilon )\]](https://intuit.ru//sites/default/files/tex_cache/289d94c020da7f16a5a30c55e74bfc9d.png)