Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Найти абсолютные значения коэффициентов характеристического уравнения 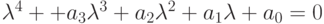 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 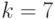 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 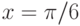 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 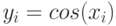 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью только из одной урны извлечены 2 белых шара?
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Задана функция двух переменных: .Имеется условие:
.Имеется условие: .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 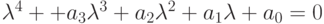 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 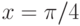 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 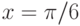 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 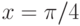 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 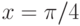 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 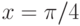 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 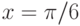 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 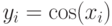 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 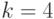 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 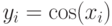 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 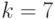 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 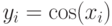 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 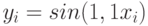 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 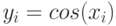 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 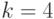 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 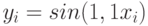 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 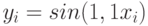 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 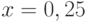 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 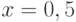 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 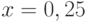 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
(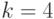 ) при
) при 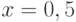 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 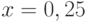 . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 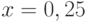 . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
(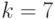 ) при
) при 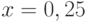 . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 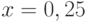 . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 5 | 5 | 7 | 1 | 6 | | 68 |
| 3 | 1 | 5 | 2 | 4 | | 48 |
| 2 | 4 | 3 | 2 | 3 | | 44 |
| 5 | 2 | 2 | 4 | 2 | | 55 |
| 2 | 3 | 6 | 3 | 1 | | 41 |
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | -1 | 3 | 1 | | 5 |
| 4 | -1 | 5 | 4 | | 4 |
| 2 | -2 | 4 | 1 | | 6 |
| 1 | -4 | 5 | -1 | | 3 |
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
| 5 | 5 | 7 | 1 | 6 |
| 3 | 1 | 5 | 2 | 4 |
| 2 | 4 | 3 | 2 | 3 |
| 5 | 2 | 2 | 4 | 2 |
| 2 | 3 | 6 | 3 | 1 |
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 5-го знака после запятой (без округления).
| 5 | 5 | 7 | 1 | 6 |
| 3 | 1 | 5 | 2 | 4 |
| 2 | 4 | 3 | 2 | 3 |
| 5 | 2 | 2 | 4 | 2 |
| 2 | 3 | 6 | 3 | 1 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 3 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
| 1 | 2 | 3 | 2 | 1 | | 39 |
| 3 | 6 | 4 | 1 | 2 | | 61 |
| 2 | 3 | 2 | 6 | 2 | | 76 |
| 3 | 6 | 3 | 3 | 3 | | 75 |
| 1 | 2 | 3 | 4 | 2 | | 56 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 3 |
 | 0 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
| 1 | 2 | 3 | 2 | 1 | | 39 |
| 3 | 6 | 4 | 1 | 2 | | 61 |
| 2 | 3 | 2 | 6 | 2 | | 76 |
| 3 | 6 | 3 | 3 | 3 | | 75 |
| 1 | 2 | 3 | 4 | 2 | | 56 |
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки

. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
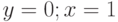
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
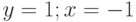
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
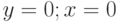
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
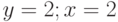
. В ответе указать значение

после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
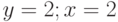
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
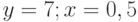
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
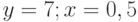
. В ответе указать значение

после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задана функция двух переменных: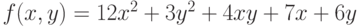 .Имеется условие:
.Имеется условие: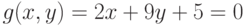 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
Задана функция двух переменных: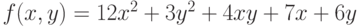 .Имеется условие:
.Имеется условие: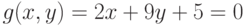 .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
Задана функция двух переменных: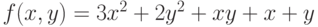 .Имеется условие:
.Имеется условие: .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
Задана функция трёх переменных: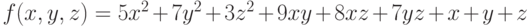 .Имеется условие:
.Имеется условие: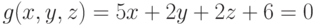 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
Задана функция трёх переменных: .Имеется условие:
.Имеется условие: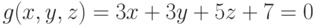 .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
Задана функция трёх переменных: .Имеется условие:
.Имеется условие: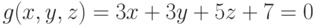 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
Задана функция двух переменных: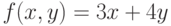 .Имеется условие:
.Имеется условие: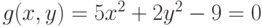 .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
Задана функция двух переменных: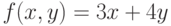 .Имеется условие:
.Имеется условие: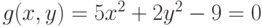 .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 2 | 6 | 0 | 1 | 72 |
| 1 | -3 | -6 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 6 | 6 | 0 | 1 | 72 |
| 1 | -4 | -9 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 1 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 4,5 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 8 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 5 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 25 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 280 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 5 | 2 | 1 | 0 | 20 |
| 0 | 3 | 1 | 0 | 1 | 35 |
| 1 | -4 | -6 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 1 | 1 | 0 | 1 | 0 | 60 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 140 |
| 1 | -6 | -8 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 6 | 4 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 40 |
| 1 | -4 | -8 | 0 | 0 | 0 |
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 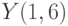 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 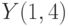 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 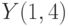 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 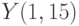 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 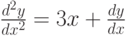 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 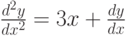 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 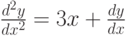 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,59375. Чему равно
равна 1,59375. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где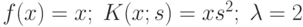 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 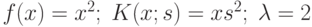 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 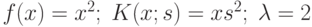 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 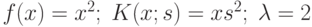 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
В урне 5 белых и 6 черных шаров. Из урны вынимают два шара. Потом возвращают их в в урну и вынимают ещё один раз шар. Найти вероятность того, что все три шара будут белыми.
В урне 5 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут одного цвета.
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 2 орла и не менее 5-ти очков на игральной кости?
Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку вдень экзамена 1/2. С какой вероятностью всё будет хорошо?
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа компьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью для обеспечения посадки достаточно будет провести ремонт двигателя? Ответ введите с точностью до 3-го знака после запятой (без округления).
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы был Тибальд родственник Монтекки. Если бы не он всё обошлось бы без крови. "Ромео и Джульетта" Шекспира была бы не трагедией, а мелодрамой с хорошим концом. С какой вероятностью это случилось бы?
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом возможны серьёзные осложнения. Какова вероятность заболевания без осложнений? Ответ округлите до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 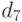 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 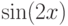 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 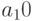 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 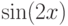 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 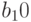 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 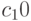 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 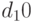 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 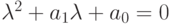 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 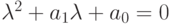 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 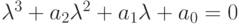 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 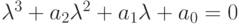 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 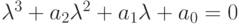 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 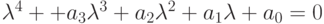 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 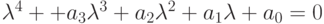 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 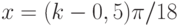 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
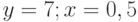
. В ответе указать значение

после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия 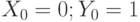 . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Задана функция двух переменных: .Имеется условие:
.Имеется условие: .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 5 |
| 0 | 6 | 5 | 0 | 1 | 45 |
| 1 | -3 | -7 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 27 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Численно решить интегральное уравнение:  , где
, где 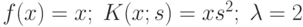 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 2 |
Задана функция двух переменных: .Имеется условие:
.Имеется условие: .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 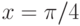 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 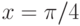 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 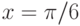 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 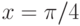 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение 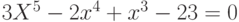 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение 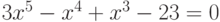 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
Задано уравнение 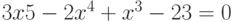 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
Задано уравнение 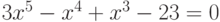 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 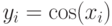 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 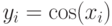 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 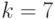 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 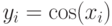 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 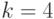 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 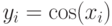 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 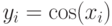 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 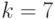 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 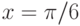 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 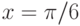 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 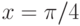 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 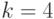 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение интеграла  методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 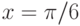 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение 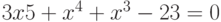 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение 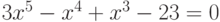 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение интеграла  методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение интеграла  методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 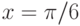 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
Вычислить значение интеграла  по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 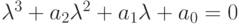 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 5-го знака после запятой (без округления).
| 2 | 4 | 3 | 3 | 2 |
| 2 | 5 | 3 | 1 | 2 |
| 1 | 4 | 1 | 4 | 3 |
| 2 | 3 | 2 | 5 | 6 |
| 1 | 4 | 5 | 6 | 8 |
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 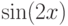 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 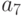 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 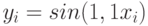 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 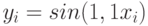 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 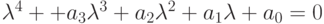 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 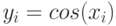 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Численно решить интегральное уравнение:  , где
, где 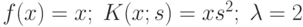 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 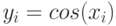 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 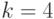 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 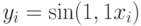 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 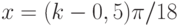 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 5 |
| 0 | 2 | 9 | 0 | 1 | 45 |
| 1 | -4 | -5 | 0 | 0 | 0 |
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задана функция трёх переменных: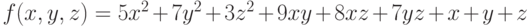 .Имеется условие:
.Имеется условие: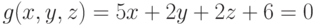 .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
Численно решить интегральное уравнение:  , где
, где . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 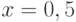 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 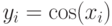 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 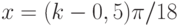 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 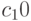 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 4 | 2 | 0 | 1 | 40 |
| 1 | -2 | -8 | 0 | 0 | 0 |
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 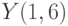 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 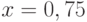 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 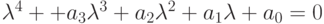 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 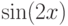 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 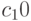 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
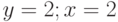
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 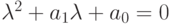 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
В урне 5 белых и 6 черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Найти вероятность того, что оба шара будут белыми.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 30 |
| 0 | 8 | 1 | 1 | 0 | 1 | 0 | 45 |
| 0 | 1 | 4 | 1 | 0 | 0 | 1 | 120 |
| 1 | -8 | -4 | -4 | 0 | 0 | 0 | 0 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 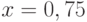 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 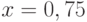 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 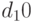 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
(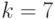 ) при
) при 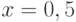 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 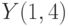 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 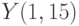 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 2 | 2 | 1 | 0 | 30 |
| 0 | 8 | 6 | 0 | 1 | 80 |
| 1 | -2 | -6 | 0 | 0 | 0 |
Найти абсолютные значения коэффициентов характеристического уравнения 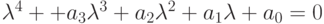 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Задана функция трёх переменных: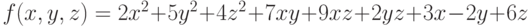 .Имеется условие:
.Имеется условие: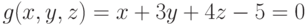 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа компьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью посадка пройдёт в штатном режиме? Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
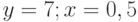
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
Задана функция двух переменных: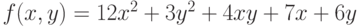 .Имеется условие:
.Имеется условие: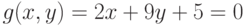 .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 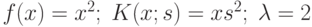 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Найти абсолютные значения коэффициентов характеристического уравнения 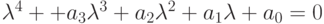 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 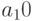 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Задана функция трёх переменных: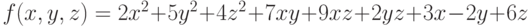 .Имеется условие:
.Имеется условие: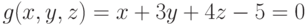 .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | -1 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
В урне 5 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут разных цветов.
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Численно решить интегральное уравнение:  , где
, где . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 2 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 96 |
| 1 | -4 | -8 | 0 | 0 | 0 |
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Задано уравнение  ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 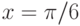 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
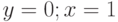
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
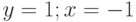
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 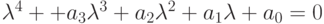 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Вычислить значение многочлена Чебышева степени  (
(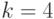 ) при
) при 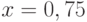 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 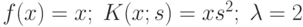 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 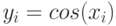 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 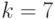 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 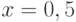 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вероятность выпадения дождя 3/4. Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку в день экзамена 1/2. С какой вероятностью придётся мокнуть под дождём на платформе в хорошем настроении, вызванном положительной оценкой на экзамене?
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью ни из одной урны не были извлечены 2 белых шара?
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Задана функция двух переменных: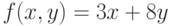 .Имеется условие:
.Имеется условие: .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 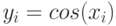 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 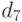 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом внаступят серьёзные осложнения. Какова вероятность осложнений? Ответ округлите до 3-го знака после запятой (без округления).
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
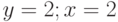
. В ответе указать значение

после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 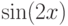 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 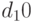 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 1 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 6 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 8 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 5 | 1 | 0 | 20 |
| 0 | 2 | 3 | 0 | 1 | 50 |
| 1 | -4 | -6 | 0 | 0 | 0 |
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 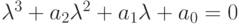 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Используя значения функции  в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 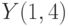 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 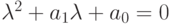 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Для дифференциального уравнения 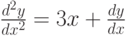 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
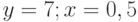
. В ответе указать значение

после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 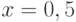 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 5 |
 | 0 |
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 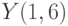 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 1 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 4 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 7 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
. В ответе указать значение

после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 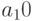 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 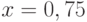 . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 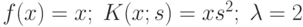 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
(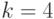 ) при
) при 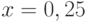 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
| 5 | 5 | 7 | 1 | 6 | | 68 |
| 3 | 1 | 5 | 2 | 4 | | 48 |
| 2 | 4 | 3 | 2 | 3 | | 44 |
| 5 | 2 | 2 | 4 | 2 | | 55 |
| 2 | 3 | 6 | 3 | 1 | | 41 |
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
Задана функция двух переменных: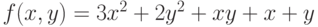 .Имеется условие:
.Имеется условие: .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 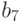 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 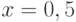 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 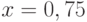 . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 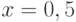 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
(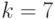 ) при
) при 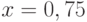 . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | -1 | 3 | 1 | | 5 |
| 4 | -1 | 5 | 4 | | 4 |
| 2 | -2 | 4 | 1 | | 6 |
| 1 | -4 | 5 | -1 | | 3 |
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 3-го знака после запятой (без округления).
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
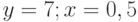
. В ответе указать значение

после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
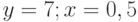
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки

. В ответе указать значение

после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
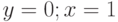
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
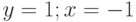
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки
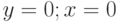
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
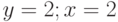
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
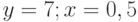
. В ответе указать значение

после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Задана функция трёх переменных: .Имеется условие:
.Имеется условие: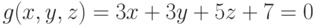 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
Задана функция двух переменных: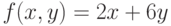 .Имеется условие:
.Имеется условие: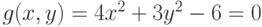 .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 6 | 5 | 0 | 1 | 96 |
| 1 | -1 | -7 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 6 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 6 | 1 | 0 | 1 | 0 | 80 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 160 |
| 1 | -4 | -8 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 2 | 1 | 0 | 25 |
| 0 | 4 | 8 | 0 | 1 | 65 |
| 1 | -6 | -8 | 0 | 0 | 0 |
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 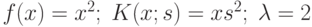 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 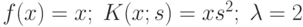 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью хотя бы из одной урны извлечены 2 белых шара?
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 2 орла и не более 5-ти очков на игральной кости?
Вероятность выпадения дождя 3/4. Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку вдень экзамена 1/2. С какой вероятностью придётся мокнуть под дождём на платформе в плохом настроении, вызванном провалом на экзамене?
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы был Тибальд родственник Монтекки. Если бы не он всё обошлось бы без крови. С какой вероятностью никакой любви не случилось бы?
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 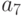 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 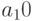 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 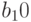 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 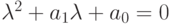 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 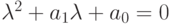 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Найти абсолютные значения коэффициентов характеристического уравнения 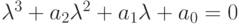 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Разложение функции  в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 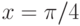 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия 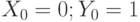 . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 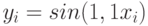 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 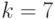 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 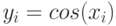 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | 2 | 3 | 2 | 1 | | 39 |
| 3 | 6 | 4 | 1 | 2 | | 61 |
| 2 | 3 | 2 | 6 | 2 | | 76 |
| 3 | 6 | 3 | 3 | 3 | | 75 |
| 1 | 2 | 3 | 4 | 2 | | 56 |
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | 2 | 3 | 2 | 1 | | 39 |
| 3 | 6 | 4 | 1 | 2 | | 61 |
| 2 | 3 | 2 | 6 | 2 | | 76 |
| 3 | 6 | 3 | 3 | 3 | | 75 |
| 1 | 2 | 3 | 4 | 2 | | 65 |
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Дан многочлен  . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки

. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки
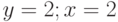
. В ответе указать значение

после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
Организовать процесс поиска минимума функции  методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
Задана функция трёх переменных: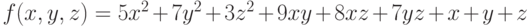 .Имеется условие:
.Имеется условие: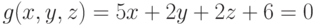 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
Задана функция двух переменных: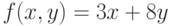 .Имеется условие:
.Имеется условие: .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 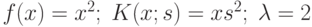 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа к омпьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью потребуется ремонт только компьютера или только навигационной системы? Ответ введите с точностью до 3-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 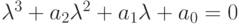 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Вычислить значение интеграла  методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 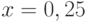 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 5 | 5 | 7 | 1 | 6 | | 68 |
| 3 | 1 | 5 | 2 | 4 | | 48 |
| 2 | 4 | 3 | 2 | 3 | | 44 |
| 5 | 2 | 2 | 4 | 2 | | 55 |
| 2 | 3 | 6 | 3 | 1 | | 41 |
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
Дана квадратная матрица. Найти значение алгебраического дополнения элемента  .
.
| 2 | 4 | 3 | 3 | 2 |
| 2 | 5 | 3 | 1 | 2 |
| 1 | 4 | 1 | 4 | 3 |
| 2 | 3 | 2 | 5 | 6 |
| 1 | 4 | 5 | 6 | 8 |
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
| 5 | 5 | 7 | 1 | 6 | | 68 |
| 3 | 1 | 5 | 2 | 4 | | 48 |
| 2 | 4 | 3 | 2 | 3 | | 44 |
| 5 | 2 | 2 | 4 | 2 | | 55 |
| 2 | 3 | 6 | 3 | 1 | | 41 |
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
Задана функция трёх переменных: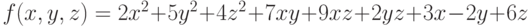 .Имеется условие:
.Имеется условие: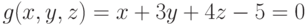 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 15 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Для дифференциального уравнения 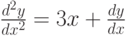 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 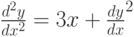 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 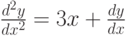 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения  задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Для дифференциального уравнения 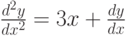 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где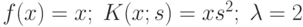 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 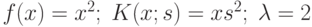 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 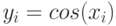 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 1 |
 | 0 |
Дан многочлен  . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Задана функция двух переменных: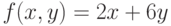 .Имеется условие:
.Имеется условие: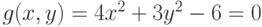 .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Численно решить интегральное уравнение:  , где
, где 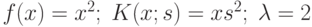 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
Подсказка. Необходимо решить матричное уравнение:

; где

. Где

. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы были друг Ромео Меркуцио и Тибальд родственник Монтекки. Если бы на их месте были бы девочки, то "Ромео и Джульетта" Шекспира была бы не трагедией, а комедией с хорошим концом. С какой вероятностью это случилось бы?
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 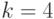 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Дана сетка значений  , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 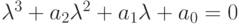 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 1 орёл и не более 4-х очков на игральной кости?
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом наступят серьёзные осложнения. Какова вероятность того, что осложнений не будет? Ответ округлите до 3-го знака после запятой (без округления).
Задана функция двух переменных: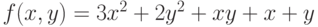 .Имеется условие:
.Имеется условие: .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
Организовать решение методом Рунге-Кутта дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 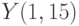 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
Найти абсолютные значения коэффициентов характеристического уравнения 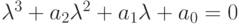 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение

.
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 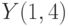 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
В урне 5 белых и 6 черных шаров. Из урны вынимают шар и возвращают его в урну. Потом вынимают ещё один раз шар. Найти вероятность того, что оба шара будут белыми.
Построить кубический сплайн  для интерполяции значений функции
для интерполяции значений функции 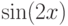 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Вычислить значение многочлена Чебышева степени  (
( ) при
) при 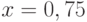 . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 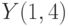 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
Организуйте методом золотого сечения поиск минимума функции  . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
Организовать решение методом Эйлера дифференциального уравнения:  . Начальные условия
. Начальные условия 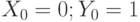 . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
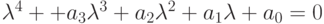 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 и
и  .
.

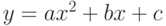 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 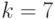 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 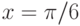 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.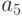
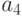





 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 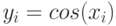 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). .Имеется условие:
.Имеется условие: .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).

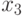
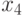
 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).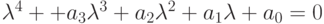 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность ![\sqrt[3]{(x/y)}](https://intuit.ru//sites/default/files/tex_cache/ed261bf3558c9f1f045ed8f21b081b56.png) .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![z=\sqrt[3]{(x/y)}+(x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/d70ccc557a88b34cddc9239e4ba3ee87.png) .
. 



 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины ![z=\sqrt[3]{(x/y)} + (x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/1bf231a6f074c556abacb56e60196ad0.png) .
. 



 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 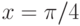 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 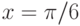 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 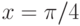 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 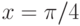 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 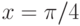 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 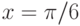 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 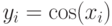 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 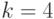 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 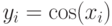 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 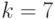 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 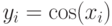 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 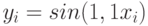 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 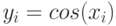 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 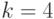 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 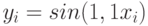 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 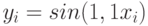 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). (
( ) при
) при 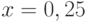 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). (
( ) при
) при 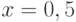 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). (
( ) при
) при 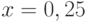 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). (
(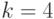 ) при
) при 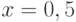 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). (
( ) при
) при 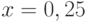 . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления). (
( ) при
) при 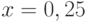 . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления). (
(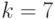 ) при
) при 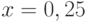 . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления). (
( ) при
) при 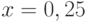 . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления). .
.



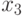


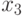
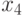


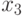
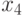
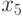




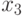


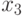
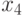


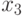
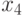
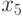
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.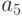
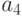





 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.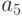
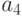





 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.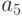
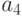





 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.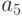
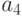





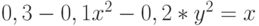
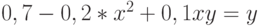
 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).

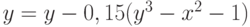
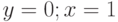 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).

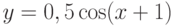
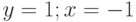 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
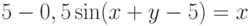
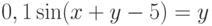
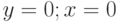 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
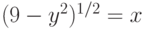
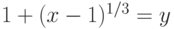
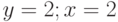 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
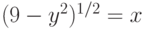
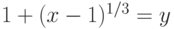
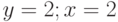 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
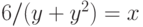
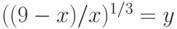
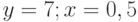 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
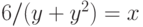
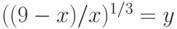
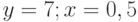 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).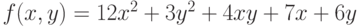 .Имеется условие:
.Имеется условие: .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).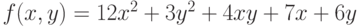 .Имеется условие:
.Имеется условие: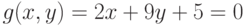 .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.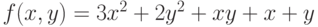 .Имеется условие:
.Имеется условие: .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака.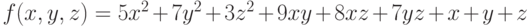 .Имеется условие:
.Имеется условие: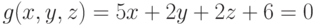 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2). .Имеется условие:
.Имеется условие: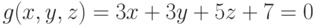 .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака. .Имеется условие:
.Имеется условие: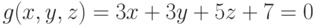 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака. .Имеется условие:
.Имеется условие: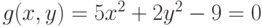 .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.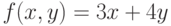 .Имеется условие:
.Имеется условие: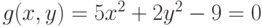 .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 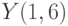 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 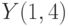 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 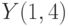 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 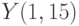 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).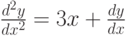 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).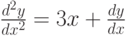 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).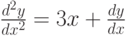 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,59375. Чему равно
равна 1,59375. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где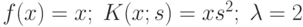 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 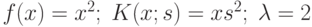 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 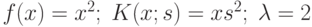 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 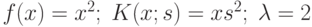 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

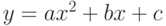 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

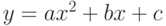 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

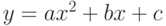 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 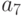 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 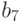 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 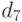 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции 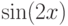 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 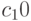 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 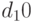 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).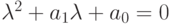 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
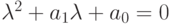 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
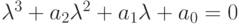 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
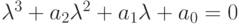 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
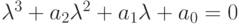 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
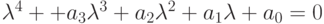 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
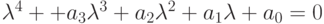 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 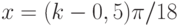 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).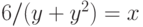
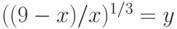
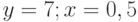 . В ответе указать значение
. В ответе указать значение  после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия 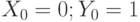 . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). .Имеется условие:
.Имеется условие: .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака. ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). , где
, где 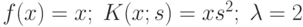 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).

 .Имеется условие:
.Имеется условие: .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления). и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти относительную погрешность
. Найти относительную погрешность 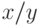 .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность ![\sqrt[3]{(x/y)}](https://intuit.ru//sites/default/files/tex_cache/ed261bf3558c9f1f045ed8f21b081b56.png) .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![z=\sqrt[3]{(x/y)}+(x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/d70ccc557a88b34cddc9239e4ba3ee87.png) .
. 



 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 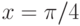 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 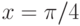 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 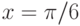 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 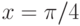 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).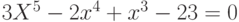 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).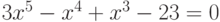 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).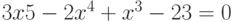 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).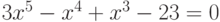 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 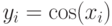 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 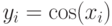 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 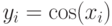 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 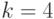 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 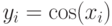 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для 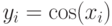 и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 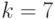 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для 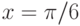 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 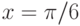 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для 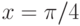 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где 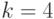 . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления). методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность ![\sqrt[3]{(x/y)}](https://intuit.ru//sites/default/files/tex_cache/ed261bf3558c9f1f045ed8f21b081b56.png) .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины ![z=\sqrt[3]{(x/y)} + (x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/1bf231a6f074c556abacb56e60196ad0.png) .
. 



 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для 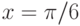 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).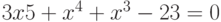 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).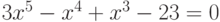 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять  . В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления). методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления). методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![z=\sqrt[3]{(x/y)}+(x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/d70ccc557a88b34cddc9239e4ba3ee87.png) .
. 



 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины ![z=\sqrt[3]{(x/y)} + (x^2+xy+y^2)/2](https://intuit.ru//sites/default/files/tex_cache/1bf231a6f074c556abacb56e60196ad0.png) .
. 



 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
. 



 и
и  . Найти относительную погрешность
. Найти относительную погрешность 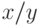 .
. 



 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 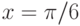 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых. по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых. и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность  .
. 



 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).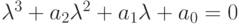 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции 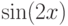 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 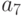 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 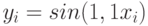 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 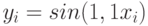 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).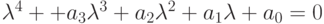 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления). и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).

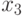
 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 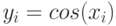 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где 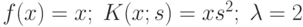 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 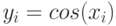 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 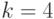 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 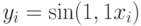 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 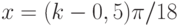 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).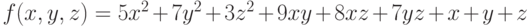 .Имеется условие:
.Имеется условие: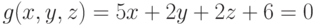 .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака. , где
, где . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

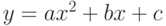 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). (
( ) при
) при 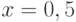 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 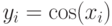 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке 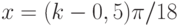 , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 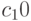 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). и
и  .
.

 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 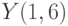 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 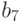 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). (
( ) при
) при 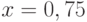 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).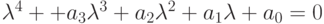 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 для интерполяции значений функции
для интерполяции значений функции 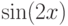 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).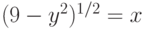
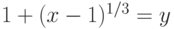
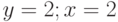 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).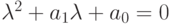 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).

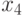
 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). (
( ) при
) при 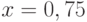 . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). (
( ) при
) при  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). и
и  .
.

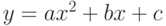 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 (
(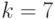 ) при
) при 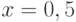 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 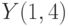 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 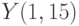 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).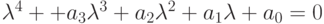 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
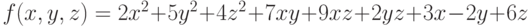 .Имеется условие:
.Имеется условие: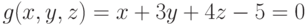 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака. градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).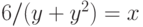
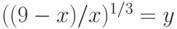
 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.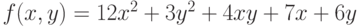 .Имеется условие:
.Имеется условие: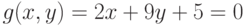 .Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.Найти значение условного экстремума. Ответ — с точностью до 3-го знака. методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). , где
, где 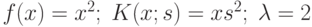 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
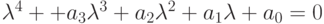 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 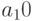 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.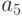
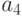





 .Имеется условие:
.Имеется условие: .Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.



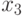
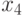
 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.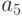
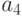





 , где
, где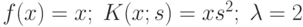 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
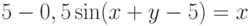
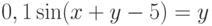
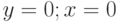 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления). в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 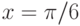 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
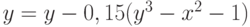
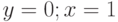 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).

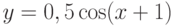
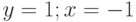 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).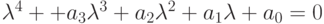 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 (
(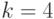 ) при
) при 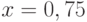 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления). , где
, где 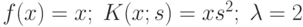 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 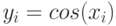 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).

 (
( ) при
) при 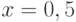 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).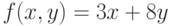 .Имеется условие:
.Имеется условие: .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака. , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 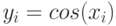 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 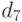 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.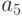
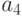





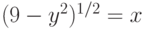
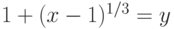
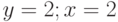 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции 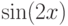 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). и
и  .
.

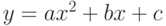 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). и
и  .
.

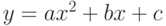 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
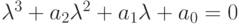 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 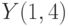 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).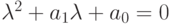 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
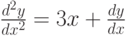 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).

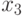
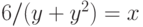
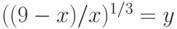
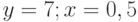 . В ответе указать значение
. В ответе указать значение  после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). (
( ) при
) при 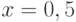 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).

 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 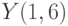 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).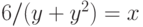
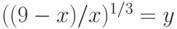
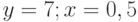 . В ответе указать значение
. В ответе указать значение  после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). (
( ) при
) при 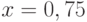 . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где 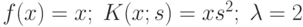 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 (
(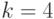 ) при
) при 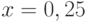 . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления). .
. . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).

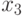
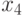
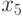
 , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.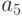
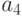





 , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
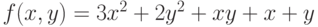 .Имеется условие:
.Имеется условие: .Найти при каких значениях
.Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака. методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). (
( ) при
) при 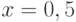 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). (
( ) при
) при 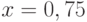 . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления). (
( ) при
) при 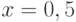 . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления). (
(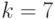 ) при
) при 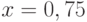 . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).

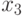


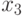
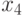


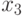
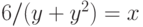
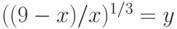
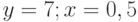 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
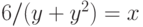
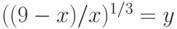
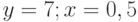 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
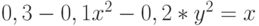
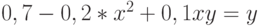
 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).

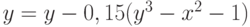
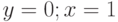 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).

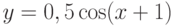
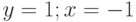 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
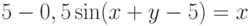
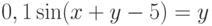
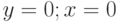 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
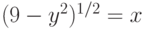
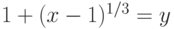
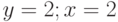 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
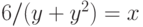
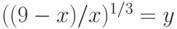
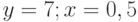 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). .Имеется условие:
.Имеется условие: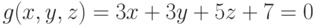 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).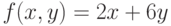 .Имеется условие:
.Имеется условие: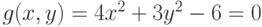 .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака. . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где 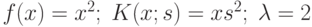 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 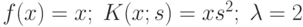 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 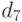 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 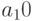 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение 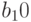 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).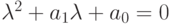 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
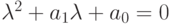 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
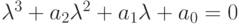 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для 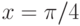 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия 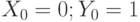 . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 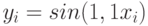 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 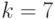 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 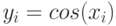 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.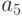
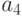





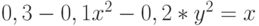
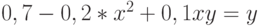
 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
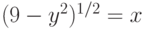
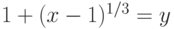
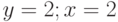 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления). методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).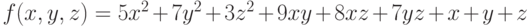 .Имеется условие:
.Имеется условие: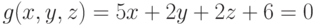 .Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.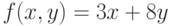 .Имеется условие:
.Имеется условие: .Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.Найти положение условных экстремумов. Ответ — с точностью до 3-го знака. . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления). , где
, где  . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 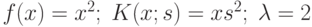 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
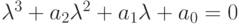 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления). (
( ) при
) при 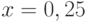 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). .
.

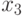
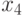
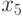
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.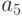
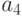





 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления. . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).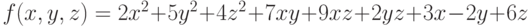 .Имеется условие:
.Имеется условие: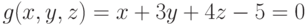 .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).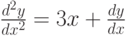 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).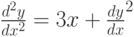 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).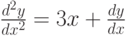 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).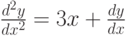 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления). , где
, где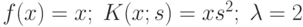 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 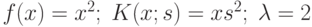 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для 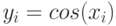 и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).

 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.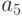
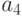





 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.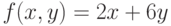 .Имеется условие:
.Имеется условие: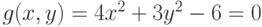 .Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака. . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). , где
, где 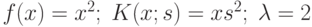 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 и
и  .
.

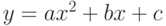 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.

 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где 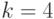 . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления). , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).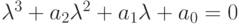 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.


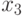
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). и
и  .
.

 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
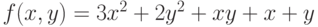 .Имеется условие:
.Имеется условие: .Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3). . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение 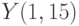 . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).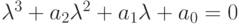 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы: .
.
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение 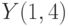 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). для интерполяции значений функции
для интерполяции значений функции 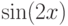 на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). (
( ) при
) при 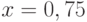 . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления). . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение 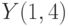 . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления). . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.