Матрицу плотности чистого состояния 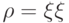 унитарный оператор переводит в матрицу:
унитарный оператор переводит в матрицу:
(Отметьте один правильный вариант ответа.)
Варианты ответа
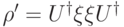
 (Верный ответ)
(Верный ответ)
нет верного ответа

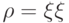 унитарный оператор переводит в матрицу:
унитарный оператор переводит в матрицу: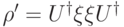
 (Верный ответ)
(Верный ответ)
 , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 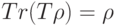 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), то задаваемый изоморфизм имеет вид:
), то задаваемый изоморфизм имеет вид: разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 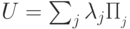 ,
,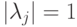 , то
, то 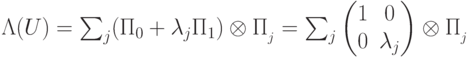 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  ,
,  соответствует повороту вокруг оси X на:
соответствует повороту вокруг оси X на: , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: для квантового состояния, задаваемого матрицей плотности
для квантового состояния, задаваемого матрицей плотности  и подпространства
и подпространства  :
: