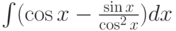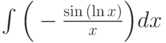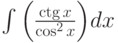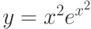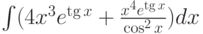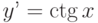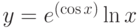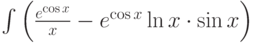Найти первообразную функции (неопределённый интеграл)
Найдите общее решение дифференциального уравнения:
Найти первообразную функции (неопределённый интеграл)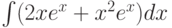
Найдите общее решение дифференциального уравнения: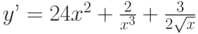
Найти производную функции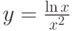
Найти производную функции
Найдите общее решение дифференциального уравнения: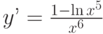
Найдите общее решение дифференциального уравнения:
Найти производную функции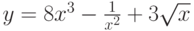
Найти производную функции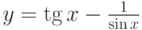
Найти производную функции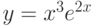
Найти производную функции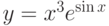
Найти производную функции
Найти производную функции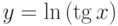
Найти производную функции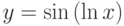
Найти производную функции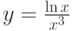
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)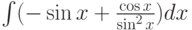
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)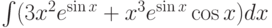
Найти первообразную функции (неопределённый интеграл)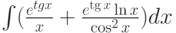
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)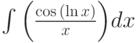
Найти первообразную функции (неопределённый интеграл)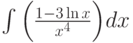
Найдите общее решение дифференциального уравнения: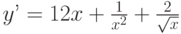
Найдите общее решение дифференциального уравнения: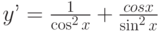
Найдите общее решение дифференциального уравнения: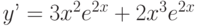
Найдите общее решение дифференциального уравнения: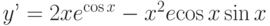
Найдите общее решение дифференциального уравнения: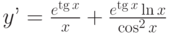
Найдите общее решение дифференциального уравнения:
Найдите общее решение дифференциального уравнения: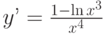
Найти производную функции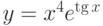
Найти первообразную функции (неопределённый интеграл)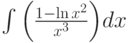
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Найти уравнение вида:  , которому удовлетворят следующие три корня:
, которому удовлетворят следующие три корня:
В ответе указать значение
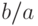
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение А.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
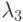
.
Решение дифференциального уравнения задано в параметрической форме: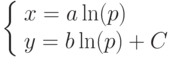 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
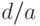
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

. Решить задачу Коши. В ответе привести значение
.
Вычислить значение определителя Вронского для x=0. 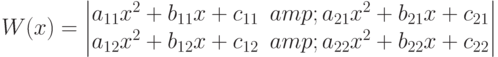
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: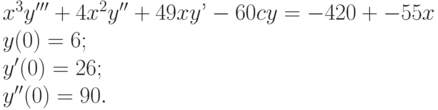 Показать, что решение задачи имеет вид:
Показать, что решение задачи имеет вид:
 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
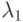
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
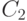
.
Решение дифференциального уравнения задано в параметрической форме: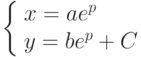 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение: 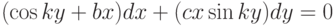
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 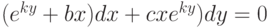
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 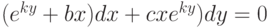
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 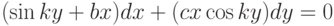
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 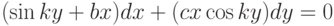
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 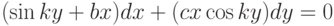
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 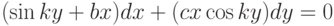
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 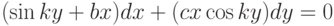
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 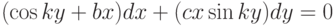
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
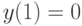
.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Решение дифференциального уравнения задано в параметрической форме: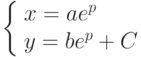 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: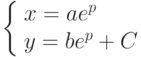 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: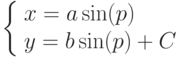 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: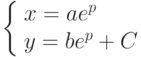 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: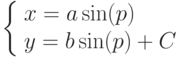 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: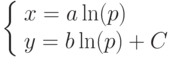 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: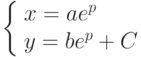 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Вычислить значение определителя Вронского для x=0. 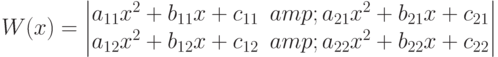
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=0. 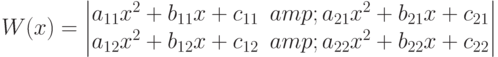
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Вычислить значение определителя Вронского для x=0. 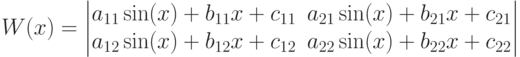
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=0. 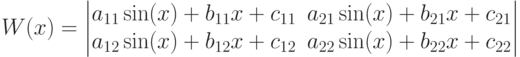
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Вычислить значение определителя Вронского для x=1. 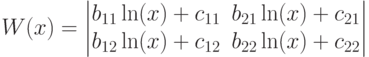
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=1. 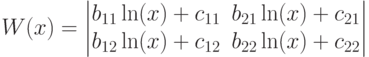
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Вычислить значение определителя Вронского для x=0. 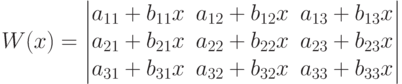
| a11 | 3 |
| b11 | 5 |
| a12 | 4 |
| b12 | 1 |
| a13 | 6 |
| b13 | 7 |
| a21 | 2 |
| b21 | 6 |
| a22 | 8 |
| b22 | 2 |
| a23 | 4 |
| b23 | 8 |
| a31 | 2 |
| b31 | 4 |
| a32 | 6 |
| b32 | 3 |
| a33 | 5 |
| b33 | 6 |
Вычислить значение производной определителя Вронского для x=0. 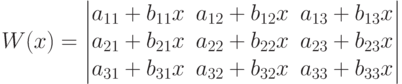
| a11 | 3 |
| b11 | 5 |
| a12 | 4 |
| b12 | 1 |
| a13 | 6 |
| b13 | 7 |
| a21 | 2 |
| b21 | 6 |
| a22 | 8 |
| b22 | 2 |
| a23 | 4 |
| b23 | 8 |
| a31 | 2 |
| b31 | 4 |
| a32 | 6 |
| b32 | 3 |
| a33 | 5 |
| b33 | 6 |
Найти корни характеристического уравнения: 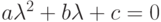 . В ответе указать наименьший из корней.
. В ответе указать наименьший из корней.
Найти корни характеристического уравнения: 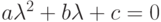 . В ответе указать наименьший из корней.
. В ответе указать наименьший из корней.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наименьший из них.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать средний по величине из них.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наибольший из них.
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
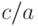
.
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
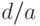
.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
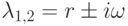
. В ответе указать значение r.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
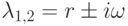
. В ответе указать значение

.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

. v – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
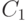
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
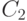
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
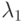
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
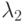
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
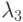
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
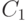
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
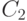
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
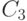
.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение A.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение B.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
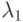
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
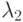
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
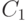
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
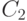
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение А.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение В.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
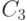
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
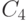
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
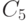
.
Вычислить значение производной определителя Вронского для x=1. 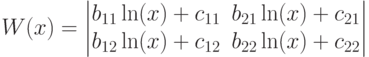
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
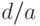
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
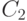
.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
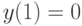
.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
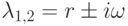
. В ответе указать значение

.
Вычислить значение производной определителя Вронского для x=0. 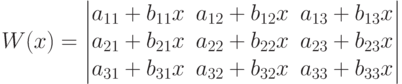
| a11 | 2 |
| b11 | 1 |
| a12 | 2 |
| b12 | 4 |
| a13 | 3 |
| b13 | 7 |
| a21 | 4 |
| b21 | 2 |
| a22 | 3 |
| b22 | 5 |
| a23 | 3 |
| b23 | 1 |
| a31 | 1 |
| b31 | 2 |
| a32 | 4 |
| b32 | 2 |
| a33 | 6 |
| b33 | 2 |
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
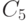
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: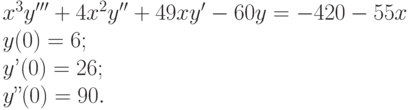 Показать, что решение задачи имеет вид:
Показать, что решение задачи имеет вид:
 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
Задано уравнение: 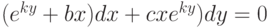
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Найти производную функции
Решение дифференциального уравнения задано в параметрической форме: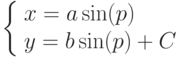 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наибольший из них.
Решение дифференциального уравнения задано в параметрической форме: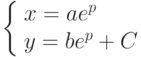 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Найти производную функции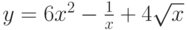
Задано уравнение: 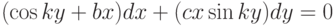
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать средний по величине из них.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
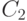
.
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
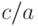
.
Найти производную функции
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
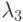
.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение A.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
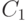
.
Найти производную функции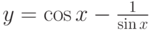
Найти производную функции
Найти производную функции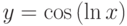
Найти первообразную функции (неопределённый интеграл)![\int( 40x^4+\frac{3}{x^4}+\frac{1}{\sqrt[3] x^2})dx](https://intuit.ru//sites/default/files/tex_cache/f6d10a5a98bdb76ec7e8faf5cfd31e76.png)
Найти первообразную функции (неопределённый интеграл)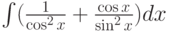
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)
Найдите общее решение дифференциального уравнения:![y’=40x^4+\frac{3}{x^4}+\frac{1}{\sqrt[3] {x^2}}](https://intuit.ru//sites/default/files/tex_cache/1063d80d994755326312e4247bfe8530.png)
Найдите общее решение дифференциального уравнения: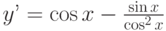
Найдите общее решение дифференциального уравнения: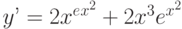
Найдите общее решение дифференциального уравнения: 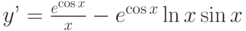
Найдите общее решение дифференциального уравнения:
Найдите общее решение дифференциального уравнения:
Задано уравнение: 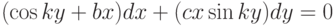
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 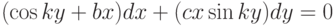
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 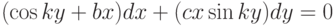
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 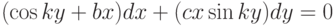
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 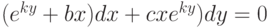
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Решение дифференциального уравнения задано в параметрической форме: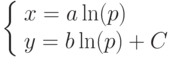 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: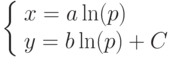 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: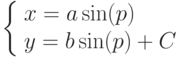 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: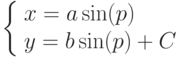 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Вычислить значение производной определителя Вронского для x=0. 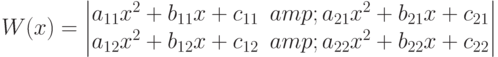
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=0. 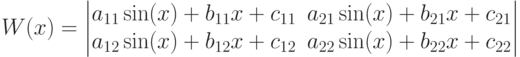
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=1. 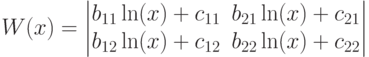
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Вычислить значение определителя Вронского для x=0. 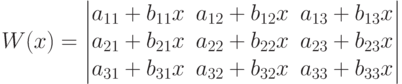
| a11 | 2 |
| b11 | 1 |
| a12 | 2 |
| b12 | 4 |
| a13 | 3 |
| b13 | 7 |
| a21 | 4 |
| b21 | 2 |
| a22 | 3 |
| b22 | 5 |
| a23 | 3 |
| b23 | 1 |
| a31 | 1 |
| b31 | 2 |
| a32 | 4 |
| b32 | 2 |
| a33 | 6 |
| b33 | 2 |
Найти корни характеристического уравнения: 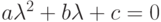 . В ответе указать наименьший из корней.
. В ответе указать наименьший из корней.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наименьший из них.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наибольший из них.
Найти уравнение вида:  , которому удовлетворят следующие три корня:
, которому удовлетворят следующие три корня:
В ответе указать значение
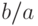
.
Найти уравнение вида:  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня:
В ответе указать значение
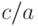
.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значение его кратного корня.
Найти производную функции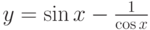
Найдите общее решение дифференциального уравнения: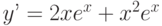
Задано уравнение: 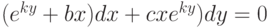
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:


– нумеруются в порядке возрастания. В ответе указать значение
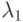
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Решение дифференциального уравнения задано в параметрической форме: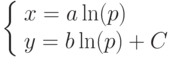 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Найдите общее решение дифференциального уравнения:
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение В.
Найдите общее решение дифференциального уравнения:
Задано уравнение: 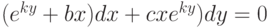
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Найти производную функции![y=8x^5-\frac{1}{x^3}+3\sqrt[3]{x}](https://intuit.ru//sites/default/files/tex_cache/73d43b01543380c8f147c386c924fa57.png)
Найти производную функции
Найти производную функции
Найти первообразную функции (неопределённый интеграл)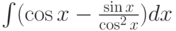
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)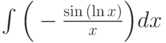
Найдите общее решение дифференциального уравнения:
Задано уравнение: 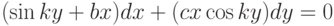
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Решение дифференциального уравнения задано в параметрической форме: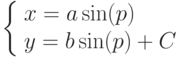 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: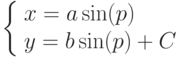 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: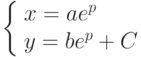 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Вычислить значение определителя Вронского для x=0. 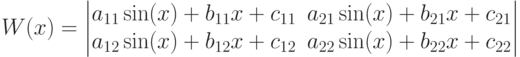
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Вычислить значение производной определителя Вронского для x=0. 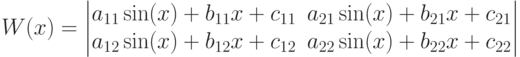
| a11 | 3 |
| b11 | 4 |
| c11 | 5 |
| a12 | 6 |
| b12 | 7 |
| c12 | 6 |
| a21 | 5 |
| b21 | 4 |
| c21 | 3 |
| a22 | 4 |
| b22 | 6 |
| c22 | 5 |
Вычислить значение определителя Вронского для x=0. 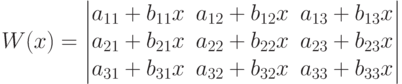
| a11 | 5 |
| b11 | 7 |
| a12 | 2 |
| b12 | 3 |
| a13 | 1 |
| b13 | 2 |
| a21 | 9 |
| b21 | 2 |
| a22 | 4 |
| b22 | 3 |
| a23 | 7 |
| b23 | 1 |
| a31 | 4 |
| b31 | 3 |
| a32 | 2 |
| b32 | 4 |
| a33 | 1 |
| b33 | 7 |
Найти корни характеристического уравнения: 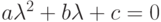 . . В ответе указать наименьший из корней.
. . В ответе указать наименьший из корней.
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать средний по величине из них.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
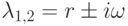
. В ответе указать значение r.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
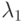
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
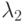
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
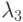
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
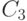
.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение B.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
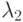
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение А.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
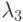
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
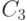
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 83 |
| c | -126 |
| A | -378 |
| B | -172 |
| F | 9 |
| G | 44 |
| H | 198 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
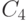
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение В.
Вычислить значение производной определителя Вронского для x=0. 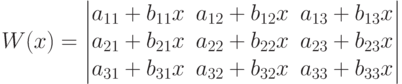
| a11 | 5 |
| b11 | 7 |
| a12 | 2 |
| b12 | 3 |
| a13 | 1 |
| b13 | 2 |
| a21 | 9 |
| b21 | 2 |
| a22 | 4 |
| b22 | 3 |
| a23 | 7 |
| b23 | 1 |
| a31 | 4 |
| b31 | 3 |
| a32 | 2 |
| b32 | 4 |
| a33 | 1 |
| b33 | 7 |
Решение дифференциального уравнения задано в параметрической форме: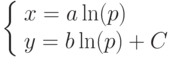 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
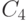
.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Найти корни характеристического уравнения: 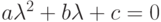 . В ответе указать наибольший из корней.
. В ответе указать наибольший из корней.
Задано уравнение: 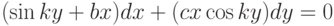
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
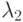
.
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)
Найти первообразную функции (неопределённый интеграл)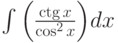
Найдите общее решение дифференциального уравнения:
Задано уравнение: 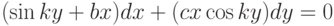
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение: 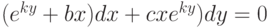
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Решение дифференциального уравнения задано в параметрической форме: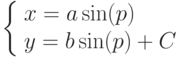 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Вычислить значение определителя Вронского для x=0. 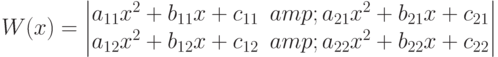
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Вычислить значение определителя Вронского для x=1. 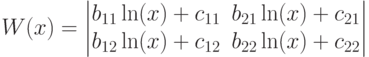
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Найти корни характеристического уравнения: 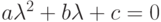 . В ответе указать наименьший из корней.
. В ответе указать наименьший из корней.
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение B.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
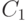
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
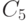
.
Вычислить значение производной определителя Вронского для x=0. 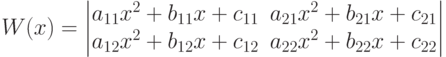
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение
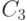
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
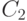
.
Задано уравнение: 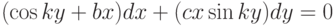
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 94 |
| c | -160 |
| A | -800 |
| B | -396 |
| F | 15 |
| G | 82 |
| H | 404 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Найти производную функции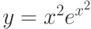
Найти первообразную функции (неопределённый интеграл)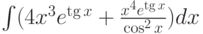
Найдите общее решение дифференциального уравнения: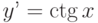
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
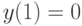
.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
Вычислить значение определителя Вронского для x=1. 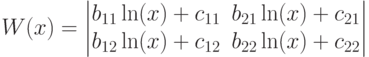
| a11 | 1 |
| b11 | 2 |
| c11 | 7 |
| a12 | 5 |
| b12 | 8 |
| c12 | 3 |
| a21 | 9 |
| b21 | 3 |
| c21 | 8 |
| a22 | 8 |
| b22 | 2 |
| c22 | 5 |
Задано характеристическое уравнение:  .
.
Найти его корни. В ответе указать наименьший из них.
Найти уравнение вида:  , которому удовлетворят следующие три корня:
, которому удовлетворят следующие три корня:
В ответе указать значение
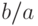
.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
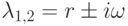
. В ответе указать значение r.
Задано неоднородное линейное дифференциальное уравнение: 
Показать, что общее решение уравнения имеет вид:

. В ответе указать значение A.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
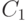
.
Задана задача Коши для неоднородного линейного дифференциального уравнения:
| a | 4 |
| b | 49 |
| c | -60 |
| A | -420 |
| B | -55 |
| F | 6 |
| G | 26 |
| H | 90 |
Показать, что решение задачи имеет вид:


– нумеруются в порядке возрастания.В ответе привести значение

.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
Найти производную функции
Найти первообразную функции (неопределённый интеграл)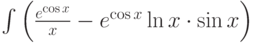
Задано уравнение вида: 
Показать, что общее решение имеет вид:

Где C – произвольная постоянная. В ответе указать значение

.
Вычислить значение определителя Вронского для x=0. 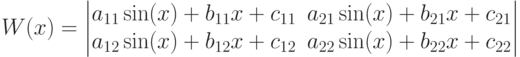
| a11 | 5 |
| b11 | 4 |
| c11 | 2 |
| a12 | 6 |
| b12 | 7 |
| c12 | 8 |
| a21 | 3 |
| b21 | 8 |
| c21 | 3 |
| a22 | 8 |
| b22 | 3 |
| c22 | 2 |
Дано уравнение  .
.
Найти значение его кратного корня.
Дано уравнение  .
.
Найдите кратный корень. В ответе укажите его кратность.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
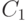
.
Задана задача Коши для неоднородного линейного дифференциального уравнения: 
Показать, что общее решение уравнения имеет вид:

.

– нумеруются в порядке возрастания. В ответе указать значение
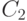
.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
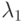
.
Решение дифференциального уравнения задано в параметрической форме: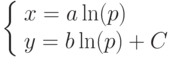 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: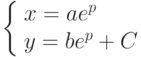 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Решение дифференциального уравнения задано в параметрической форме: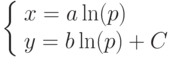 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
В ответе укажите недостающий параметр.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
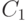
.
Задано уравнение: 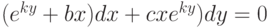
Показать, что интегрирующий множитель имеет вид:

В ответе указать значение m.
Дано уравнение  .
.
Найти значения пары комплексно-сопряжённых корней:
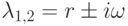
. В ответе указать значение

.
Найдите общее решение дифференциального уравнения:
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
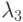
.
Дано уравнение  .
.
Найти значение его кратного корня.
Дана задача Коши: 
Убедитесь, что общее решение однородного уравнения имеет вид:

.

– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
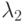
.
Известно, что функции  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 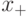 .
.

 . В ответе указать значение А.
. В ответе указать значение А.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 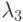 .
.
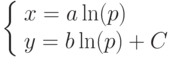 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа. . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня: 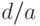 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 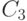 .
.

 . Решить задачу Коши. В ответе привести значение
. Решить задачу Коши. В ответе привести значение 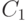 .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 
 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 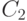 .
.
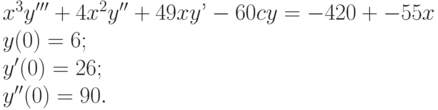 Показать, что решение задачи имеет вид:
Показать, что решение задачи имеет вид:
 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  Найти замену переменных
Найти замену переменных 
 где (x+) и (y+) постоянные величины.
где (x+) и (y+) постоянные величины.  .
.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 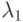 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 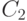 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 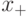 .
.
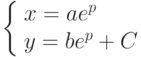 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.
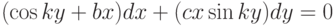
 В ответе указать значение m.
В ответе указать значение m.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 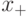 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 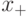 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 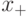 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 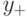 .
.
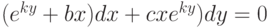
 В ответе указать значение m.
В ответе указать значение m.
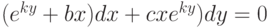
 В ответе указать значение m.
В ответе указать значение m.
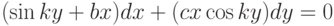
 В ответе указать значение m.
В ответе указать значение m.
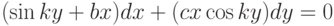
 В ответе указать значение m.
В ответе указать значение m.
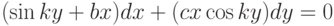
 В ответе указать значение m.
В ответе указать значение m.
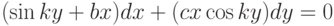
 В ответе указать значение m.
В ответе указать значение m.
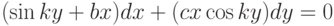
 В ответе указать значение m.
В ответе указать значение m.
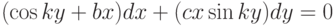
 В ответе указать значение m.
В ответе указать значение m.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию 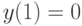 .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 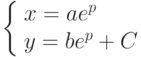 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.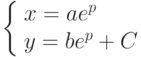 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.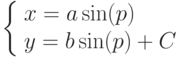 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.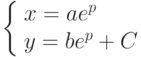 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.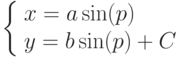 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.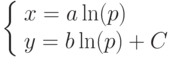 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.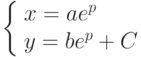 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.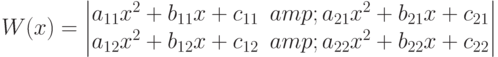
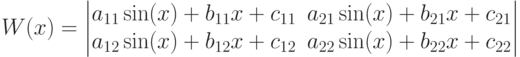
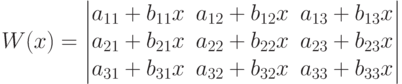
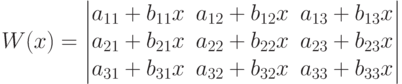
 .
.  .
.  .
.  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня: 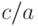 .
.
 . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня: 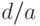 .
.
 .
. 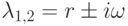 . В ответе указать значение r.
. В ответе указать значение r.
 .
. 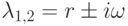 . В ответе указать значение
. В ответе указать значение  .
.

 . v – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
. v – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 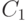 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 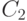 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 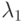 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 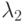 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 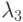 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 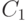 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 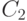 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 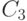 .
.

 . В ответе указать значение A.
. В ответе указать значение A.

 . В ответе указать значение B.
. В ответе указать значение B.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 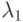 .
.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 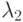 .
.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 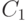 .
.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 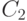 .
.

 . В ответе указать значение А.
. В ответе указать значение А.

 . В ответе указать значение В.
. В ответе указать значение В.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 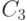 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 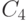 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 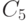 .
.
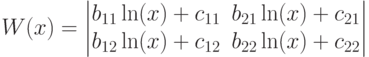

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 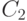 .
.

 Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию 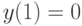 .
.
 .
. 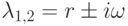 . В ответе указать значение
. В ответе указать значение  .
.
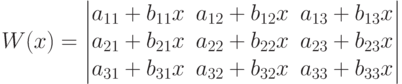


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 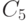 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
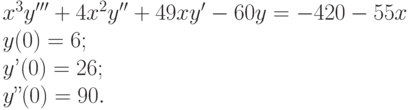 Показать, что решение задачи имеет вид:
Показать, что решение задачи имеет вид:
 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
. 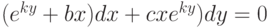
 В ответе указать значение m.
В ответе указать значение m.
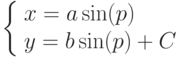 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа. .
. 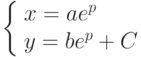 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.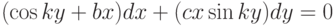
 В ответе указать значение m.
В ответе указать значение m.
 .
. 
 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 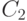 .
.
 . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня: 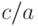 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 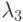 .
.

 . В ответе указать значение A.
. В ответе указать значение A.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 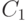 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 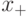 .
.
 Найти замену переменных
Найти замену переменных 
 где (x+) и (y+) постоянные величины.
где (x+) и (y+) постоянные величины.  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 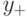 .
.
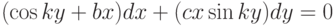
 В ответе указать значение m.
В ответе указать значение m.
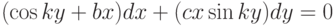
 В ответе указать значение m.
В ответе указать значение m.
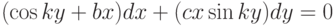
 В ответе указать значение m.
В ответе указать значение m.
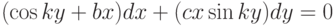
 В ответе указать значение m.
В ответе указать значение m.
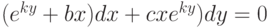
 В ответе указать значение m.
В ответе указать значение m.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.
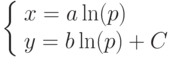 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.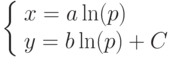 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.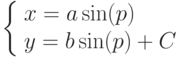 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.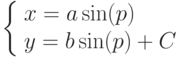 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа. 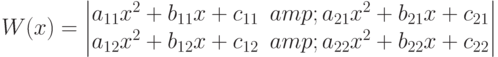
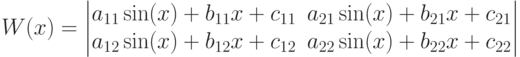
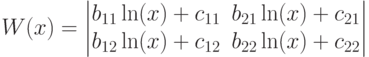
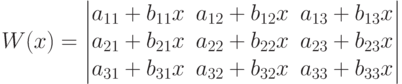
 .
.  .
.  . , которому удовлетворят следующие три корня:
. , которому удовлетворят следующие три корня: 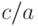 .
.
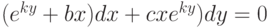
 В ответе указать значение m.
В ответе указать значение m.


 – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 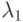 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
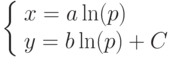 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
 . В ответе указать значение В.
. В ответе указать значение В.
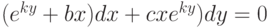
 В ответе указать значение m.
В ответе указать значение m.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  Найти замену переменных
Найти замену переменных 
 где (x+) и (y+) постоянные величины.
где (x+) и (y+) постоянные величины.  .
.
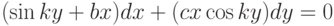
 В ответе указать значение m.
В ответе указать значение m.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 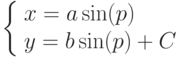 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.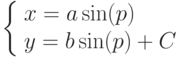 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.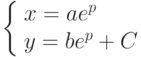 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.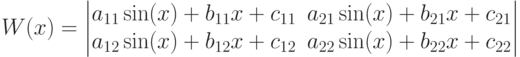
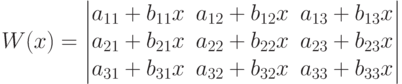
 .
.  .
. 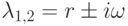 . В ответе указать значение r.
. В ответе указать значение r.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 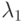 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 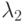 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 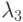 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 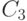 .
.

 . В ответе указать значение B.
. В ответе указать значение B.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 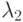 .
.

 . В ответе указать значение А.
. В ответе указать значение А.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 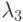 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 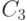 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.

 . В ответе указать значение В.
. В ответе указать значение В.
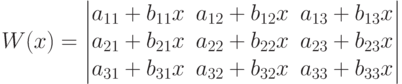
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
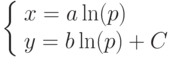 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа. и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 

 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение 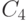 .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
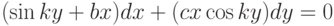
 В ответе указать значение m.
В ответе указать значение m.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 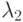 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 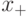 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины.  .
.
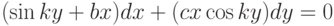
 В ответе указать значение m.
В ответе указать значение m.
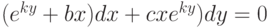
 В ответе указать значение m.
В ответе указать значение m.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 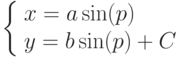 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
 . В ответе указать значение B.
. В ответе указать значение B.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 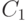 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
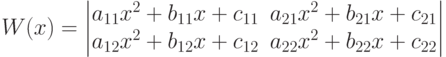


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение  .
.
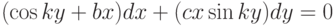
 В ответе указать значение m.
В ответе указать значение m.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 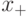 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 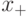 .
.

 Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию
Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию 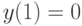 .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.  .
.  .
. 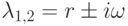 . В ответе указать значение r.
. В ответе указать значение r.

 . В ответе указать значение A.
. В ответе указать значение A.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 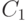 .
.


 – нумеруются в порядке возрастания.В ответе привести значение
– нумеруются в порядке возрастания.В ответе привести значение  .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 
 Где C – произвольная постоянная. В ответе указать значение
Где C – произвольная постоянная. В ответе указать значение  .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 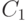 .
.

 .
.  – нумеруются в порядке возрастания. В ответе указать значение
– нумеруются в порядке возрастания. В ответе указать значение 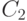 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 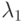 .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 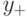 .
.
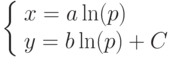 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.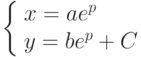 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.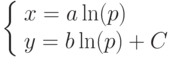 Условие задачи Коши имеет вид:
Условие задачи Коши имеет вид:  .Здесь C произвольная константа.
.Здесь C произвольная константа.
 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 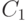 .
.
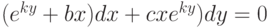
 В ответе указать значение m.
В ответе указать значение m.
 .
.  . В ответе указать значение
. В ответе указать значение  .
.
 Найти замену переменных
Найти замену переменных 
 где
где  и
и  постоянные величины.
постоянные величины. 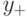 .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 
 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 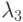 .
.

 .
.  – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение
– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение 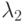 .
.
 и
и  являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка. 


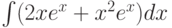
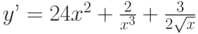
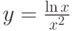

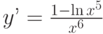

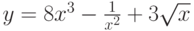
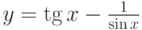
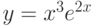
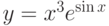

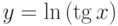
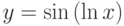
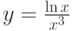

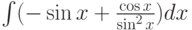

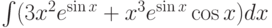
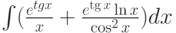

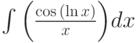
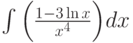
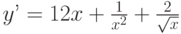
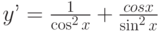
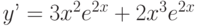
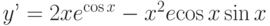
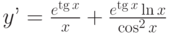

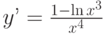
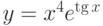
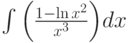
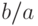 .
.
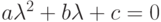 . В ответе указать наименьший из корней.
. В ответе указать наименьший из корней. 
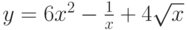

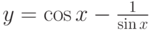

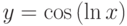
![\int( 40x^4+\frac{3}{x^4}+\frac{1}{\sqrt[3] x^2})dx](https://intuit.ru//sites/default/files/tex_cache/f6d10a5a98bdb76ec7e8faf5cfd31e76.png)
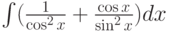



![y’=40x^4+\frac{3}{x^4}+\frac{1}{\sqrt[3] {x^2}}](https://intuit.ru//sites/default/files/tex_cache/1063d80d994755326312e4247bfe8530.png)
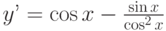
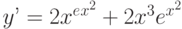
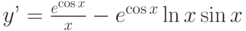


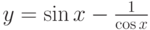
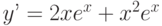


![y=8x^5-\frac{1}{x^3}+3\sqrt[3]{x}](https://intuit.ru//sites/default/files/tex_cache/73d43b01543380c8f147c386c924fa57.png)