Математический анализ - ответы
Количество вопросов - 986
Функция  – рациональная (т.е. вида P(x)/Q(x), где
– рациональная (т.е. вида P(x)/Q(x), где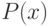 и
и 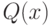 – полиномы). Является ли функция
– полиномы). Является ли функция  непрерывной на промежутке
непрерывной на промежутке  ?
?
Как ведет себя функция  в точке
в точке  , если известно, что все ее низшие производные равны нулю:
, если известно, что все ее низшие производные равны нулю:  вплоть до производной
вплоть до производной 
Функция  – полином 25 степени, имеющий ровно 25 действительных различных корней. Сколько корней имеет функция
– полином 25 степени, имеющий ровно 25 действительных различных корней. Сколько корней имеет функция 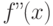 ?
?
При помощи какой подстановки можно вычислить следующий интеграл 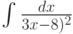 ? Выберите соответствующую вспомогательную переменную из списка
? Выберите соответствующую вспомогательную переменную из списка
Вычислите разность между верхней и нижней интегральной суммой для интеграла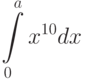 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 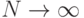
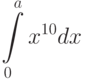
Вычислите разность между верхней и нижней интегральной суммой для интеграла (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 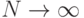

Функция  – рациональная (т.е. вида
– рациональная (т.е. вида  , где
, где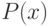 и
и 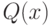 – полиномы). Является ли функция
– полиномы). Является ли функция  непрерывной на промежутке
непрерывной на промежутке 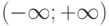 ?
?
Как ведет себя функция  в точке
в точке  , если известно, что все ее низшие производные равны нулю:
, если известно, что все ее низшие производные равны нулю:  вплоть до производной
вплоть до производной 
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси  ), заданной уравнением
), заданной уравнением 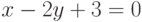 ? Ответ введите с помощью рациональной дроби.
? Ответ введите с помощью рациональной дроби.
Найдите ординату точки, в которой прямая, заданная уравнением 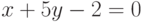 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
Для кривой 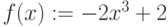 постройте секущую через точки
постройте секущую через точки 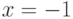 и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
. Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
Для кривой 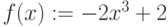 постройте секущую через точки
постройте секущую через точки 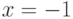 и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Для кривой 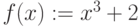 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Для кривой 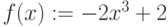 найдите уравнение касательной
найдите уравнение касательной  в точке
в точке 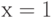 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 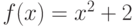 , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равен наклон касательной? Ответ введите в виде целого числа.
. Чему равен наклон касательной? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 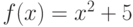 , которая будет параллельная прямой
, которая будет параллельная прямой 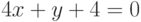 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  (число
(число  )? Ответ введите в виде целого числа.
)? Ответ введите в виде целого числа.
Пользуясь определением производной, найдите производную функции 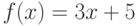 в точке
в точке 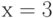 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Найдите точку, в которой касательная к графику функции 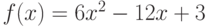 проходит горизонтально. Ответ введите в виде целого числа.
проходит горизонтально. Ответ введите в виде целого числа.
Пользуясь определением производной, найдите наклон графика функции 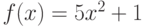 в точке
в точке 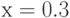 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равна его скорость через две секунды после начала движения, т.е. при
. Чему равна его скорость через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Известно, что в точке  предел функции
предел функции  равен 0, а предел функции
равен 0, а предел функции 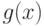 равен 1. Найдите предел
равен 1. Найдите предел 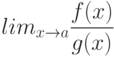 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
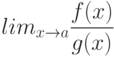
Известно, что в точке a предел функции  равен 10, а предел функции
равен 10, а предел функции 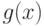 равен -20. Найдите предел
равен -20. Найдите предел  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.

Каким значением следует доопределить функцию 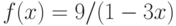 в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
Функция задана следующим образом: Найдите значение параметров
Найдите значение параметров  и
и  , при котором функция
, при котором функция  будет и непрерывной в точке
будет и непрерывной в точке  , и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.
, и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.

Найдите значение выражения (разность значений производной функции в двух точках) 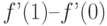 , если функция
, если функция  определяется как
определяется как 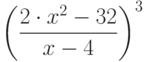
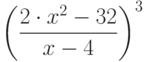
Используя дифференцирование неявной функции, найдите значение производной 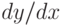 , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 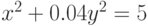 . Найти
. Найти 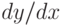 в точке
в точке  ,
, 
Используя дифференцирование неявной функции, найдите значение ее второй производной  , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 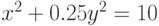 . Найти
. Найти 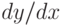 в точке
в точке 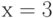 ,
, 
Рассмотрим функцию  . Известно, что в точке
. Известно, что в точке  значение функции
значение функции  , а ее производная
, а ее производная 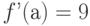 . Чему в той же точке
. Чему в той же точке  равна производная функции
равна производная функции ![[f(x)]^3](https://intuit.ru//sites/default/files/tex_cache/84bcfbd049b302d2a926507ddcd4968f.png)
Аппроксимируйте функцию  в точке
в точке  линейной функцией и вычислите, чему равно линеаризованное приближение в точке
линейной функцией и вычислите, чему равно линеаризованное приближение в точке 

Построив линеаризацию функции 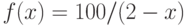 в точке
в точке  , отыщите погрешность линейной аппроксимации в точке
, отыщите погрешность линейной аппроксимации в точке 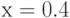 . Ответ введите, округлив полученную погрешность до целого числа.
. Ответ введите, округлив полученную погрешность до целого числа.
Аппроксимируйте функцию 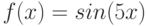 в точке
в точке  линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
В специальной теории относительности масса предмета, который двигается со скоростью 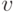 дается формулой:
дается формулой: . Где
. Где  – скорость света,
– скорость света,  – масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,5% по сравнению с массой покоя? Для ответа введите отношение
– масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,5% по сравнению с массой покоя? Для ответа введите отношение
c/v
, округленное до целого числа.Найдите соотношение высоты H и радиуса основания R цилиндрической банки (т.е. цилиндра без верхней крышки), если известно, что:- ее внутренний объем максимален среди всех возможных банок с одинаковой площадью поверхности А. Подсказка: Используйте R в качестве переменнойВведите значение H, при условии, что 
Пусть дана окружность 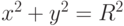 и точка
и точка  , лежащая на оси
, лежащая на оси 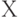 . Найдите на окружности точку
. Найдите на окружности точку  , ближайшую к
, ближайшую к  , вычислите расстояние между точками
, вычислите расстояние между точками  и
и  , если
, если 
Необходимо огородить прямоугольный участок земли площадью 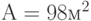 , который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
, который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
Для функции 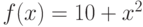 , на интервале
, на интервале 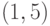 , найдите явно точку
, найдите явно точку  , существование которой гарантируется теоремой о среднем значении.
, существование которой гарантируется теоремой о среднем значении.
Для функции 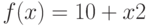 , на интервале
, на интервале 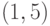 , найдите явно значение функции
, найдите явно значение функции  в точке, существование которой гарантируется теоремой о среднем значении.
в точке, существование которой гарантируется теоремой о среднем значении.
Найдите производную неявно заданной функции 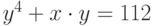 в точке
в точке 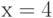 ,
,  . Ответ введите в форме простой дроби, например, 1/3.
. Ответ введите в форме простой дроби, например, 1/3.
Пусть функция  задана так:
задана так: 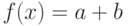 при
при 
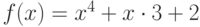 при
при 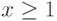 Укажите пару значений
Укажите пару значений  и
и  , при которых функция
, при которых функция  будет дифференцируемой. В качестве ответа введите их произведение (т.е. число
будет дифференцируемой. В качестве ответа введите их произведение (т.е. число  ).
).
Вычислите предел. Подсказка: Придумайте функцию  , вычисление производной которой позволит найти предел.
, вычисление производной которой позволит найти предел. 
Ракета взлетает с космодрома вертикально вверх, причем ее высота изменяется со временем по закону  (в метрах). Наблюдатель, находясь на поверхности Земли в 500 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через
(в метрах). Наблюдатель, находясь на поверхности Земли в 500 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через 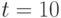 сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
Известно, что функция  в точке
в точке  принимает значение
принимает значение 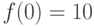 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 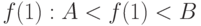 . Найдите
. Найдите 
Известно, что функция  в точке
в точке  принимает значение
принимает значение 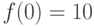 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 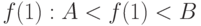 . Найдите
. Найдите 
Вычислите приближенное значение выражения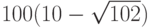 , не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
, не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
Известно, что площадь прямоугольника равна 25 кв.м. Меньше какого целого числа не может быть периметр прямоугольника (в м)?
Постройте равнобедренный треугольник (сторона двух сторон которого равна 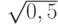 ) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
Вычислите первообразную  . Введите коэффициент старшей степени полинома, который получается в результате.
. Введите коэффициент старшей степени полинома, который получается в результате.
Вычислите первообразную полинома 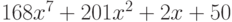 . Введите коэффициент при первой степени x полинома, который получается в результате.
. Введите коэффициент при первой степени x полинома, который получается в результате.
Решите дифференциальное уравнение 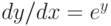 с начальным условием
с начальным условием  . Убедитесь в том, что решение определено для всех
. Убедитесь в том, что решение определено для всех 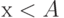 . Введите число
. Введите число  .
.
Решите дифференциальное уравнение 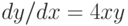 с начальным условием
с начальным условием  . Убедитесь в том, что решение имеет вид
. Убедитесь в том, что решение имеет вид 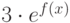 . Вычислите, чему равно значение
. Вычислите, чему равно значение  в точке
в точке 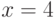 .
.
Посчитайте, чему равна правая интегральная сумма для интеграла 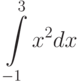 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
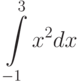
Посчитайте, чему равна правая интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Вычислите разность между верхней и нижней интегральной суммой для интеграла 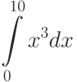 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для 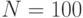 ?
?
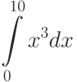
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 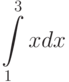
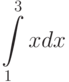
Посчитайте, чему равна левая интегральная сумма для интеграла 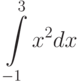 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
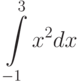
Посчитайте, чему равна правая интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Вычислите разность между верхней и нижней интегральной суммой для интеграла 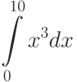 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
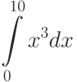
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 

Вычислите объемы двух тел вращения. Первое образовано вращением области, ограниченной параболой 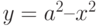 и прямой
и прямой  вокруг оси
вокруг оси  . Второе образовано вращением области, ограниченной параболой
. Второе образовано вращением области, ограниченной параболой 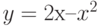 и прямой
и прямой  , также вокруг оси
, также вокруг оси  .Во сколько раз объем первого тела больше объема второго?
.Во сколько раз объем первого тела больше объема второго? 
Вычислите разность между верхней и нижней интегральной суммой для интеграла 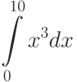 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
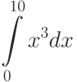
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 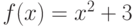 , которая будет параллельная прямой
, которая будет параллельная прямой 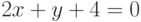 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  (число
(число  )? Ответ введите в виде целого числа.
)? Ответ введите в виде целого числа.
Решите дифференциальное уравнение 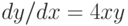 с начальным условием
с начальным условием  . Убедитесь в том, что решение имеет вид
. Убедитесь в том, что решение имеет вид 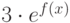 . Вычислите, чему равно значение
. Вычислите, чему равно значение  в точке
в точке 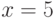 .
.
Пусть дана окружность 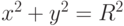 и точка
и точка  , лежащая на оси
, лежащая на оси 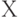 . Найдите на окружности точку
. Найдите на окружности точку  , ближайшую к
, ближайшую к  , вычислите расстояние между точками
, вычислите расстояние между точками  и
и  , если
, если 
Необходимо огородить прямоугольный участок земли площадью  , который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
, который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
Известно, что в точке  предел функции
предел функции  равен 100, а предел функции
равен 100, а предел функции 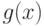 равен 20. Найдите предел
равен 20. Найдите предел 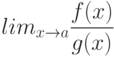 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
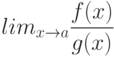
Рассмотрим функцию  . Известно, что в точке
. Известно, что в точке  значение функции
значение функции  , а ее производная
, а ее производная 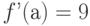 . Чему в той же точке
. Чему в той же точке  равна производная функции
равна производная функции ![[f(x)]^5](https://intuit.ru//sites/default/files/tex_cache/f2050f4d985765fbc3fcdb664705bdfb.png)
Найдите ординату точки, в которой прямая, заданная уравнением 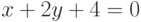 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 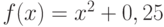 , которая будет параллельная прямой
, которая будет параллельная прямой 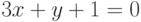 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  (число
(число  )? Ответ введите в виде целого числа.
)? Ответ введите в виде целого числа.
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси 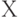 ), заданной уравнением
), заданной уравнением 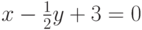 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите ординату точки, в которой прямая, заданная уравнением 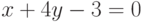 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
Для кривой  постройте секущую через точки
постройте секущую через точки  и
и 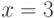 . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
. Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
Для кривой 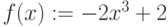 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Для кривой  найдите уравнение касательной
найдите уравнение касательной  в точке
в точке 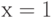 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 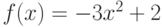 , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равен наклон касательной? Ответ введите в виде целого числа.
. Чему равен наклон касательной? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 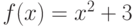 , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  (число
(число  )? Ответ введите в виде целого числа.
)? Ответ введите в виде целого числа.
Пользуясь определением производной, найдите производную функции 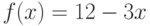 в точке
в точке 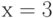 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Пользуясь определением производной, найдите наклон графика функции 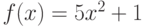 в точке
в точке  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Объект движется по закону 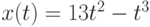 . Чему равна его скорость через две секунды после начала движения, т.е. при
. Чему равна его скорость через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Объект движется по закону 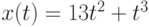 . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Известно, что в точке  предел функции
предел функции  равен 4, а предел функции
равен 4, а предел функции 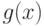 равен 2. Найдите предел
равен 2. Найдите предел 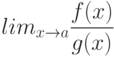 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
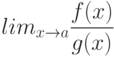
Известно, что в точке a предел функции  равен 3, а предел функции
равен 3, а предел функции 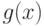 равен 1. Найдите предел
равен 1. Найдите предел  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.

Функции  и g(x) непрерывны на открытом промежутке (a,b). Является ли их произведение, т.е. функция
и g(x) непрерывны на открытом промежутке (a,b). Является ли их произведение, т.е. функция 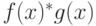 непрерывной на этом же промежутке (a,b)?
непрерывной на этом же промежутке (a,b)?
Каким значением следует доопределить функцию 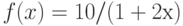 в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
Функция задана следующим образом: Найдите значение параметров
Найдите значение параметров  и
и  , при котором функция
, при котором функция 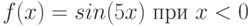 будет и непрерывной в точке
будет и непрерывной в точке  , и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.
, и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.

Найдите значение выражения (разность значений производной функции в двух точках) 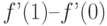 , если функция
, если функция  определяется как
определяется как 

Используя дифференцирование неявной функции, найдите значение производной 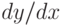 , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 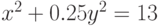 . Найти
. Найти 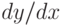 в точке
в точке 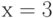 ,
, 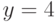
Аппроксимируйте функцию  в точке
в точке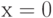 линейной функцией и вычислите, чему равно линеаризованное приближение в точке
линейной функцией и вычислите, чему равно линеаризованное приближение в точке 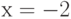

Построив линеаризацию функции  в точке
в точке  , отыщите погрешность линейной аппроксимации в точке
, отыщите погрешность линейной аппроксимации в точке  . Ответ введите, округлив полученную погрешность до целого числа.
. Ответ введите, округлив полученную погрешность до целого числа.
Аппроксимируйте функцию  в точке
в точке  линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
В специальной теории относительности масса предмета, который двигается со скоростью 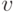 дается формулой:
дается формулой: . Где
. Где  – скорость света,
– скорость света,  – масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,1% по сравнению с массой покоя? Для ответа введите отношение
– масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,1% по сравнению с массой покоя? Для ответа введите отношение
c/v
, округленное до целого числа.Найдите соотношение высоты H и радиуса основания R цилиндрической банки (т.е. цилиндра без верхней крышки), если известно, что:- ее внутренний объем максимален среди всех возможных банок с одинаковой площадью поверхности А. Подсказка: Используйте R в качестве переменнойВведите значение H, при условии, что 
Пусть дана окружность 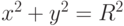 и точка
и точка  , лежащая на оси
, лежащая на оси  . Найдите на окружности точку
. Найдите на окружности точку  , ближайшую к
, ближайшую к  , вычислите расстояние между точками
, вычислите расстояние между точками  и
и  , если
, если 
Необходимо огородить прямоугольный участок земли площадью  , который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
, который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
Как ведет себя функция  в точке
в точке  , если известно, что все ее низшие производные равны нулю:
, если известно, что все ее низшие производные равны нулю:  вплоть до производной
вплоть до производной 
Для функции 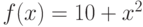 , на интервале
, на интервале  , найдите явно точку
, найдите явно точку  , существование которой гарантируется теоремой о среднем значении.
, существование которой гарантируется теоремой о среднем значении.
Для функции 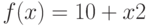 , на интервале
, на интервале 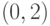 , найдите явно значение функции
, найдите явно значение функции  в точке, существование которой гарантируется теоремой о среднем значении.
в точке, существование которой гарантируется теоремой о среднем значении.
Функция  – полином 25 степени, имеющий ровно 25 действительных различных корней. Сколько корней имеет функция
– полином 25 степени, имеющий ровно 25 действительных различных корней. Сколько корней имеет функция  ?
?
Найдите производную неявно заданной функции 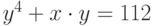 в точке
в точке 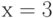 ,
,  . Ответ введите в форме простой дроби, например, 1/3.
. Ответ введите в форме простой дроби, например, 1/3.
Пусть функция  задана так:
задана так: 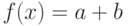 при
при 
 при
при 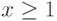 Укажите пару значений
Укажите пару значений  и
и  , при которых функция
, при которых функция  будет дифференцируемой. В качестве ответа введите их произведение (т.е. число
будет дифференцируемой. В качестве ответа введите их произведение (т.е. число  ).
).
Вычислите предел. Подсказка: Придумайте функцию  , вычисление производной которой позволит найти предел.
, вычисление производной которой позволит найти предел. 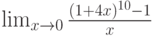
Ракета взлетает с космодрома вертикально вверх, причем ее высота изменяется со временем по закону  (в метрах). Наблюдатель, находясь на поверхности Земли в 1000 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через
(в метрах). Наблюдатель, находясь на поверхности Земли в 1000 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через 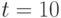 сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
Известно, что функция  в точке
в точке  принимает значение
принимает значение 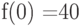 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 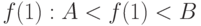 . Найдите
. Найдите 
Известно, что функция  в точке
в точке  принимает значение
принимает значение 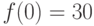 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 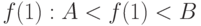 . Найдите
. Найдите 
Вычислите приближенное значение выражения , не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
, не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
Постройте равнобедренный треугольник (сторона двух сторон которого равна  ) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
Вычислите первообразную 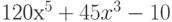 . Введите коэффициент старшей степени полинома, который получается в результате.
. Введите коэффициент старшей степени полинома, который получается в результате.
Вычислите первообразную полинома 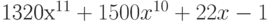 . Введите коэффициент при первой степени x полинома, который получается в результате.
. Введите коэффициент при первой степени x полинома, который получается в результате.
При помощи какой подстановки можно вычислить следующий интеграл 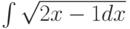 ? Выберите соответствующую вспомогательную переменную из списка
? Выберите соответствующую вспомогательную переменную из списка
Решите дифференциальное уравнение 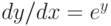 с начальным условием
с начальным условием  . Убедитесь в том, что решение определено для всех
. Убедитесь в том, что решение определено для всех 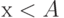 . Введите число
. Введите число  .
.
Решите дифференциальное уравнение 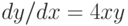 с начальным условием
с начальным условием  . Убедитесь в том, что решение имеет вид
. Убедитесь в том, что решение имеет вид 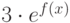 . Вычислите, чему равно значение
. Вычислите, чему равно значение  в точке
в точке  .
.
Посчитайте, чему равна верхняя интегральная сумма для интеграла 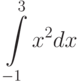 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
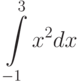
Вычислите разность между верхней и нижней интегральной суммой для интеграла (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 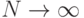

Посчитайте, чему равна правая интегральная сумма для интеграла 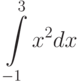 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
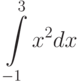
Вычислите разность между верхней и нижней интегральной суммой для интеграла 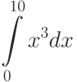 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
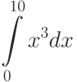
Вычислите разность между верхней и нижней интегральной суммой для интеграла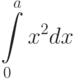 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 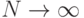
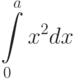
Вычислите объемы двух тел вращения. Первое образовано вращением области, ограниченной параболой 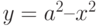 и прямой
и прямой  вокруг оси
вокруг оси  . Второе образовано вращением области, ограниченной параболой
. Второе образовано вращением области, ограниченной параболой 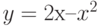 и прямой
и прямой  , также вокруг оси
, также вокруг оси  .Во сколько раз объем первого тела больше объема второго?
.Во сколько раз объем первого тела больше объема второго? 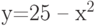
Решите дифференциальное уравнение 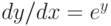 с начальным условием
с начальным условием  . Убедитесь в том, что решение определено для всех
. Убедитесь в том, что решение определено для всех 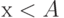 . Введите число
. Введите число  .
.
Рассмотрим функцию  . Известно, что в точке
. Известно, что в точке  значение функции
значение функции  , а ее производная
, а ее производная 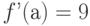 . Чему в той же точке
. Чему в той же точке  равна производная функции
равна производная функции ![[f(x)]^2](https://intuit.ru//sites/default/files/tex_cache/538e7e357a46f0d2c071a59c982bb512.png)
Для кривой  постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Найдите ординату точки, в которой прямая, заданная уравнением 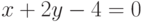 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
Для кривой 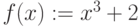 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
. Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
Для кривой 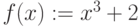 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Для кривой 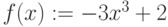 найдите уравнение касательной
найдите уравнение касательной  в точке
в точке 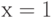 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции  , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равен наклон касательной? Ответ введите в виде целого числа.
. Чему равен наклон касательной? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 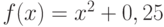 , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  (число
(число  )? Ответ введите в виде целого числа.
)? Ответ введите в виде целого числа.
Найдите точку, в которой касательная к графику функции  проходит горизонтально. Ответ введите в виде целого числа.
проходит горизонтально. Ответ введите в виде целого числа.
Пользуясь определением производной, найдите наклон графика функции  в точке
в точке 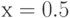 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Известно, что в точке a предел функции  равен 3, а a предел функции
равен 3, а a предел функции 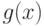 равен 2. Найдите предел
равен 2. Найдите предел  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.

Функция задана следующим образом: Найдите значение параметров
Найдите значение параметров  и
и  , при котором функция
, при котором функция 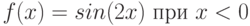 будет и непрерывной в точке
будет и непрерывной в точке  , и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.
, и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.

Используя дифференцирование неявной функции, найдите значение производной 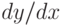 , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 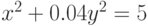 . Найти
. Найти 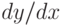 в точке
в точке 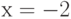 ,
, 
Используя дифференцирование неявной функции, найдите значение ее второй производной  , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 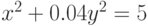 . Найти
. Найти 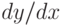 в точке
в точке  ,
, 
Аппроксимируйте функцию  в точке
в точке  линейной функцией и вычислите, чему равно линеаризованное приближение в точке
линейной функцией и вычислите, чему равно линеаризованное приближение в точке 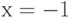

Аппроксимируйте функцию 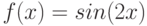 в точке
в точке  линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
Постройте квадратичную аппроксимацию функции  в точке
в точке  , т.е. функцией
, т.е. функцией 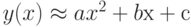 . Чему равно значение
. Чему равно значение 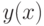 в точке
в точке 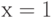 ?
?
В специальной теории относительности масса предмета, который двигается со скоростью 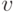 дается формулой:
дается формулой: . Где
. Где  – скорость света,
– скорость света,  – масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 1% по сравнению с массой покоя? Для ответа введите отношение
– масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 1% по сравнению с массой покоя? Для ответа введите отношение
c/v
, округленное до целого числа.Найдите соотношение высоты H и радиуса основания R цилиндрической банки (т.е. цилиндра без верхней крышки), если известно, что:- ее внутренний объем максимален среди всех возможных банок с одинаковой площадью поверхности А. Подсказка: Используйте R в качестве переменнойВведите значение H, при условии, что 
Необходимо огородить прямоугольный участок земли площадью  , который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
, который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
Как ведет себя функция  в точке
в точке  , если известно, что все ее низшие производные равны нулю:
, если известно, что все ее низшие производные равны нулю:  вплоть до производной
вплоть до производной 
Для функции 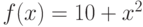 , на интервале
, на интервале 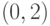 , найдите явно точку
, найдите явно точку  , существование которой гарантируется теоремой о среднем значении.
, существование которой гарантируется теоремой о среднем значении.
Найдите производную неявно заданной функции 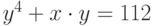 в точке
в точке 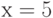 ,
, 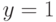 . Ответ введите в форме простой дроби, например, 1/3.
. Ответ введите в форме простой дроби, например, 1/3.
Пусть функция  задана так:
задана так: 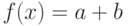 при
при 
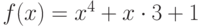 при
при 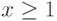 Укажите пару значений
Укажите пару значений  и
и  , при которых функция
, при которых функция  будет дифференцируемой. В качестве ответа введите их произведение (т.е. число
будет дифференцируемой. В качестве ответа введите их произведение (т.е. число  ).
).
Ракета взлетает с космодрома вертикально вверх, причем ее высота изменяется со временем по закону  (в метрах). Наблюдатель, находясь на поверхности Земли в 500 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через
(в метрах). Наблюдатель, находясь на поверхности Земли в 500 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через 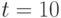 сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
Известно, что функция  в точке
в точке  принимает значение
принимает значение  и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 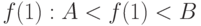 . Найдите
. Найдите 
Известно, что площадь прямоугольника равна 16 кв.м. Меньше какого целого числа не может быть периметр прямоугольника (в м)?
Вычислите первообразную 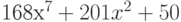 . Введите коэффициент старшей степени полинома, который получается в результате.
. Введите коэффициент старшей степени полинома, который получается в результате.
Решите дифференциальное уравнение 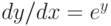 с начальным условием
с начальным условием  . Убедитесь в том, что решение определено для всех
. Убедитесь в том, что решение определено для всех 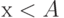 . Введите число
. Введите число  .
.
Посчитайте, чему равна нижняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.

Вычислите разность между верхней и нижней интегральной суммой для интеграла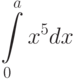 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 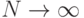
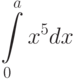
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 

Посчитайте, чему равна нижняя интегральная сумма для интеграла 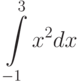 при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.
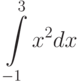
Посчитайте, чему равна нижняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.

Вычислите разность между верхней и нижней интегральной суммой для интеграла 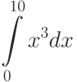 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для 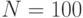 ?
?
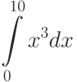
Вычислите разность между верхней и нижней интегральной суммой для интеграла (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 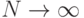

Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 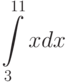
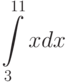
Вычислите объемы двух тел вращения. Первое образовано вращением области, ограниченной параболой 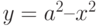 и прямой
и прямой  вокруг оси
вокруг оси  . Второе образовано вращением области, ограниченной параболой
. Второе образовано вращением области, ограниченной параболой 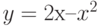 и прямой
и прямой  , также вокруг оси
, также вокруг оси  .Во сколько раз объем первого тела больше объема второго?
.Во сколько раз объем первого тела больше объема второго? 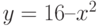
Посчитайте, чему равна верхняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Используя дифференцирование неявной функции, найдите значение ее второй производной  , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 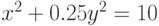 . Найти
. Найти 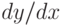 в точке
в точке 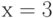 ,
, 
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси 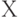 ), заданной уравнением
), заданной уравнением 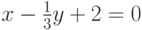 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите ординату точки, в которой прямая, заданная уравнением  , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
Для кривой 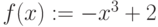 постройте секущую через точки
постройте секущую через точки  и
и 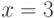 . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
. Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
Для кривой  постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Для кривой 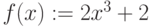 найдите уравнение касательной
найдите уравнение касательной  в точке
в точке 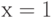 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите точку, в которой касательная к графику функции  проходит горизонтально. Ответ введите в виде целого числа.
проходит горизонтально. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Каким значением следует доопределить функцию 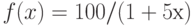 в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
Функция задана следующим образом: Найдите значение параметров
Найдите значение параметров  и
и  , при котором функция
, при котором функция  будет и непрерывной в точке
будет и непрерывной в точке  , и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.
, и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.

Используя дифференцирование неявной функции, найдите значение производной 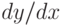 , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением  . Найти
. Найти 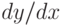 в точке
в точке  ,
, 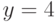
Аппроксимируйте функцию  в точке
в точке  линейной функцией и вычислите, чему равно линеаризованное приближение в точке
линейной функцией и вычислите, чему равно линеаризованное приближение в точке 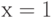

Построив линеаризацию функции 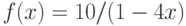 в точке
в точке  , отыщите погрешность линейной аппроксимации в точке
, отыщите погрешность линейной аппроксимации в точке 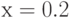 . Ответ введите, округлив полученную погрешность до целого числа.
. Ответ введите, округлив полученную погрешность до целого числа.
Для функции 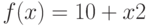 , на интервале
, на интервале 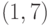 , найдите явно значение функции
, найдите явно значение функции  в точке, существование которой гарантируется теоремой о среднем значении.
в точке, существование которой гарантируется теоремой о среднем значении.
Найдите производную неявно заданной функции 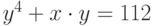 в точке
в точке  ,
,  . Ответ введите в форме простой дроби, например, 1/3.
. Ответ введите в форме простой дроби, например, 1/3.
Вычислите предел. Подсказка: Придумайте функцию  , вычисление производной которой позволит найти предел.
, вычисление производной которой позволит найти предел. 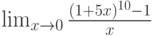
Известно, что площадь прямоугольника равна 49кв.м. Меньше какого целого числа не может быть периметр прямоугольника (в м)?
Постройте равнобедренный треугольник (сторона двух сторон которого равна 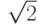 ) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
Вычислите первообразную 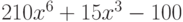 . Введите коэффициент старшей степени полинома, который получается в результате.
. Введите коэффициент старшей степени полинома, который получается в результате.
При помощи какой подстановки можно вычислить следующий интеграл  ? Выберите соответствующую вспомогательную переменную из списка
? Выберите соответствующую вспомогательную переменную из списка
Вычислите разность между верхней и нижней интегральной суммой для интеграла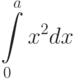 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 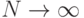
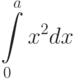
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 

Посчитайте, чему равна верхняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 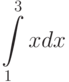
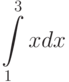
Вычислите объемы двух тел вращения. Первое образовано вращением области, ограниченной параболой 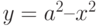 и прямой
и прямой  вокруг оси
вокруг оси  . Второе образовано вращением области, ограниченной параболой
. Второе образовано вращением области, ограниченной параболой 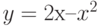 и прямой
и прямой  , также вокруг оси
, также вокруг оси  .Во сколько раз объем первого тела больше объема второго?
.Во сколько раз объем первого тела больше объема второго? 
Найдите значение выражения (разность значений производной функции в двух точках) 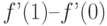 , если функция
, если функция  определяется как
определяется как 

Решите дифференциальное уравнение 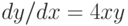 с начальным условием
с начальным условием  . Убедитесь в том, что решение имеет вид
. Убедитесь в том, что решение имеет вид 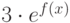 . Вычислите, чему равно значение
. Вычислите, чему равно значение  в точке
в точке 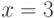 .
.
Как ведет себя функция  в точке
в точке  , если известно, что все ее низшие производные равны нулю:
, если известно, что все ее низшие производные равны нулю:  вплоть до производной
вплоть до производной 
Пользуясь определением производной, найдите наклон графика функции  в точке
в точке 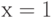 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Известно, что в точке  предел функции
предел функции  равен 7, а предел функции
равен 7, а предел функции 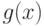 равен 1. Найдите предел
равен 1. Найдите предел 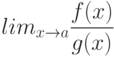 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Для кривой 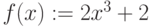 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции  , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равен наклон касательной? Ответ введите в виде целого числа.
. Чему равен наклон касательной? Ответ введите в виде целого числа.
Пользуясь определением производной, найдите производную функции 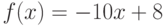 в точке
в точке 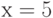 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Объект движется по закону 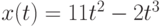 . Чему равна его скорость через две секунды после начала движения, т.е. при
. Чему равна его скорость через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите значение выражения (разность значений производной функции в двух точках) 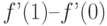 , если функция
, если функция  определяется как
определяется как 

Рассмотрим функцию  . Известно, что в точке
. Известно, что в точке  значение функции
значение функции  , а ее производная
, а ее производная 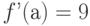 . Чему в той же точке
. Чему в той же точке  равна производная функции
равна производная функции ![[f(x)]^6](https://intuit.ru//sites/default/files/tex_cache/671cb44e788fd46cf1f5076ea145a13f.png)
Построив линеаризацию функции  в точке
в точке  , отыщите погрешность линейной аппроксимации в точке
, отыщите погрешность линейной аппроксимации в точке  . Ответ введите, округлив полученную погрешность до целого числа.
. Ответ введите, округлив полученную погрешность до целого числа.
Известно, что функция  в точке
в точке  принимает значение
принимает значение 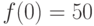 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 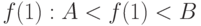 . Найдите
. Найдите 
Вычислите приближенное значение выражения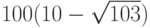 , не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
, не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
Известно, что площадь прямоугольника равна 81 кв.м. Меньше какого целого числа не может быть периметр прямоугольника (в м)?
Вычислите первообразную полинома 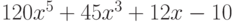 . Введите коэффициент при первой степени x полинома, который получается в результате.
. Введите коэффициент при первой степени x полинома, который получается в результате.
Посчитайте, чему равна левая интегральная сумма для интеграла 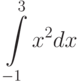 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
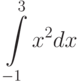
Посчитайте, чему равна верхняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Посчитайте, чему равна нижняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.

Вычислите разность между верхней и нижней интегральной суммой для интеграла 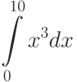 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
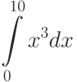
Для кривой 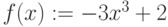 постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Каким значением следует доопределить функцию 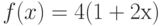 в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
Вычислите разность между верхней и нижней интегральной суммой для интеграла 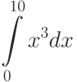 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
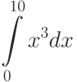
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси 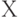 ), заданной уравнением
), заданной уравнением  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Для кривой  постройте секущую через точки
постройте секущую через точки  и
и  . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
. Чем равен наклон секущей (m)? Ответ введите в виде целого числа.
Для кривой  постройте секущую через точки
постройте секущую через точки  и
и 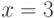 . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Известно, что в точке a предел функции  равен 0, а a предел функции
равен 0, а a предел функции 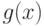 равен 1. Найдите предел
равен 1. Найдите предел  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.

Функция  непрерывна и дифференцируема в точке
непрерывна и дифференцируема в точке 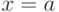 . Является ли ее производная f’(x) непрерывной в точке
. Является ли ее производная f’(x) непрерывной в точке 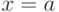 ?
?
Используя дифференцирование неявной функции, найдите значение ее второй производной  , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением  . Найти
. Найти 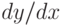 в точке
в точке  ,
, 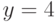
Аппроксимируйте функцию  в точке
в точке  линейной функцией и вычислите, чему равно линеаризованное приближение в точке
линейной функцией и вычислите, чему равно линеаризованное приближение в точке 

Аппроксимируйте функцию 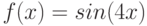 в точке
в точке  линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
В специальной теории относительности масса предмета, который двигается со скоростью 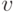 дается формулой:
дается формулой: . Где
. Где  – скорость света,
– скорость света,  – масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 2% по сравнению с массой покоя? Для ответа введите отношение
– масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 2% по сравнению с массой покоя? Для ответа введите отношение
c/v
, округленное до целого числа.Пусть дана окружность 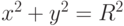 и точка
и точка  , лежащая на оси
, лежащая на оси 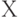 . Найдите на окружности точку
. Найдите на окружности точку  , ближайшую к
, ближайшую к  , вычислите расстояние между точками
, вычислите расстояние между точками  и
и  , если
, если 
Необходимо огородить прямоугольный участок земли площадью  , который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
, который примыкает к бесконечно длинному забору (иными словами, огородить надо только три стороны – на четвертой забор уже есть). Какова минимальная погонная длина изгороди (в м), которую необходимо построить?
Для функции 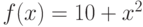 , на интервале
, на интервале 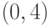 , найдите явно точку
, найдите явно точку  , существование которой гарантируется теоремой о среднем значении.
, существование которой гарантируется теоремой о среднем значении.
Ракета взлетает с космодрома вертикально вверх, причем ее высота изменяется со временем по закону  (в метрах). Наблюдатель, находясь на поверхности Земли в 300 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через
(в метрах). Наблюдатель, находясь на поверхности Земли в 300 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через 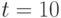 сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
Вычислите приближенное значение выражения , не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
, не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
Вычислите первообразную 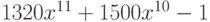 . Введите коэффициент старшей степени полинома, который получается в результате.
. Введите коэффициент старшей степени полинома, который получается в результате.
Вычислите первообразную полинома 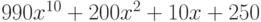 . Введите коэффициент при первой степени x полинома, который получается в результате.
. Введите коэффициент при первой степени x полинома, который получается в результате.
Решите дифференциальное уравнение 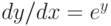 с начальным условием
с начальным условием  . Убедитесь в том, что решение определено для всех
. Убедитесь в том, что решение определено для всех 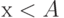 . Введите число
. Введите число  .
.
Посчитайте, чему равна верхняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Вычислите разность между верхней и нижней интегральной суммой для интеграла 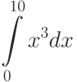 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
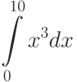
Пользуясь определением производной, найдите производную функции 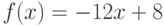 в точке
в точке  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Пусть дана окружность 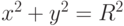 и точка
и точка  , лежащая на оси
, лежащая на оси 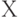 . Найдите на окружности точку
. Найдите на окружности точку  , ближайшую к
, ближайшую к  , вычислите расстояние между точками
, вычислите расстояние между точками  и
и  , если
, если 
Вычислите разность между верхней и нижней интегральной суммой для интеграла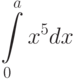 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 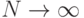
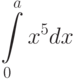
Для кривой 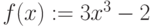 найдите уравнение касательной
найдите уравнение касательной  в точке
в точке 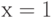 . Чему равна начальная ордината касательной
. Чему равна начальная ордината касательной  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите ординату точки, в которой прямая, заданная уравнением 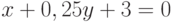 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
Для кривой 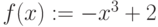 постройте секущую через точки
постройте секущую через точки  и
и 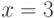 . Выпишите коэффициенты уравнения секущей
. Выпишите коэффициенты уравнения секущей  . Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
. Найдите значение ординаты в которой секущая пересечет ось ординат OY. Ответ введите в виде целого числа.
Объект движется по закону  . Чему равна его скорость через две секунды после начала движения, т.е. при
. Чему равна его скорость через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Каким значением следует доопределить функцию  в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
в точке ее устранимого разрыва, чтобы она стала непрерывной? Введите целое число.
Вычислите предел. Подсказка: Придумайте функцию  , вычисление производной которой позволит найти предел.
, вычисление производной которой позволит найти предел. 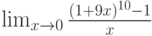
Вычислите первообразную полинома 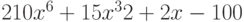 . Введите коэффициент при первой степени x полинома, который получается в результате.
. Введите коэффициент при первой степени x полинома, который получается в результате.
При помощи какой подстановки можно вычислить следующий интеграл 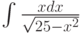 ? Выберите соответствующую вспомогательную переменную из списка
? Выберите соответствующую вспомогательную переменную из списка
Посчитайте, чему равна нижняя интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.

Вычислите разность между верхней и нижней интегральной суммой для интеграла 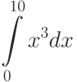 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
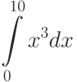
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 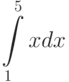
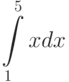
Посчитайте, чему равна левая интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Вычислите разность между верхней и нижней интегральной суммой для интеграла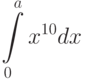 (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 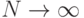
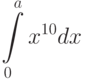
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 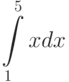
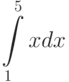
Найдите соотношение высоты H и радиуса основания R цилиндрической банки (т.е. цилиндра без верхней крышки), если известно, что:- ее внутренний объем максимален среди всех возможных банок с одинаковой площадью поверхности А. Подсказка: Используйте R в качестве переменнойВведите значение H, при условии, что 
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси  ), заданной уравнением
), заданной уравнением 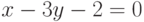 ? Ответ введите с помощью рациональной дроби.
? Ответ введите с помощью рациональной дроби.
Найдите точку, в которой касательная к графику функции 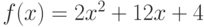 проходит горизонтально. Ответ введите в виде целого числа.
проходит горизонтально. Ответ введите в виде целого числа.
Известно, что в точке  предел функции
предел функции  равен 4, а предел функции
равен 4, а предел функции 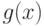 равен 1. Найдите предел
равен 1. Найдите предел 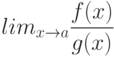 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
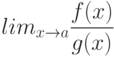
Рассмотрим функцию  . Известно, что в точке
. Известно, что в точке  значение функции
значение функции  , а ее производная
, а ее производная 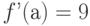 . Чему в той же точке
. Чему в той же точке  равна производная функции
равна производная функции ![[f(x)]^4](https://intuit.ru//sites/default/files/tex_cache/ae4aab18144a35da9b278c55d040e110.png)
Построив линеаризацию функции  в точке
в точке  , отыщите погрешность линейной аппроксимации в точке
, отыщите погрешность линейной аппроксимации в точке 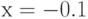 . Ответ введите, округлив полученную погрешность до целого числа.
. Ответ введите, округлив полученную погрешность до целого числа.
Для функции 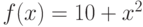 , на интервале
, на интервале 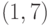 , найдите явно точку
, найдите явно точку  , существование которой гарантируется теоремой о среднем значении.
, существование которой гарантируется теоремой о среднем значении.
Функция  – полином 100 степени, имеющий ровно 100 действительных различных корней. Сколько корней имеет функция
– полином 100 степени, имеющий ровно 100 действительных различных корней. Сколько корней имеет функция  ?
?
Найдите производную неявно заданной функции 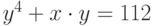 в точке
в точке 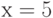 ,
,  . Ответ введите в форме простой дроби, например, 1/3.
. Ответ введите в форме простой дроби, например, 1/3.
Пусть функция  задана так:
задана так: 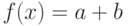 при
при 
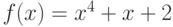 при
при 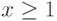 Укажите пару значений
Укажите пару значений  и
и  , при которых функция
, при которых функция  будет дифференцируемой. В качестве ответа введите их произведение (т.е. число
будет дифференцируемой. В качестве ответа введите их произведение (т.е. число  ).
).
Известно, что функция  в точке
в точке  принимает значение
принимает значение 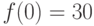 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 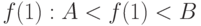 . Найдите
. Найдите 
Вычислите приближенное значение выражения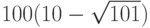 , не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
, не прибегая к калькулятору и округлив его до ближайшего целого числа. Подсказка: представьте число под корнем в виде линейной аппроксимации.
Постройте равнобедренный треугольник (сторона двух сторон которого равна 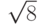 ) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
Посчитайте, чему равна нижняя интегральная сумма для интеграла 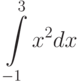 при разбиении интервала интегрирования на 4 равные части.
при разбиении интервала интегрирования на 4 равные части.
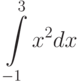
Вычислите разность между верхней и нижней интегральной суммой для интеграла 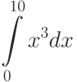 (при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для
(при условии разбиения интервала интегрирования на N равных промежутков). Чему равно значение разности для  ?
?
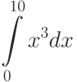
Посчитайте, чему равна верхняя интегральная сумма для интеграла 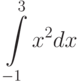 при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части
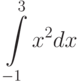
Объект движется по закону 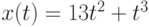 . Чему равно его ускорение через две секунды после начала движения, т.е. при
. Чему равно его ускорение через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Функции  и g(x) имеют производные в любой точке х
и g(x) имеют производные в любой точке х 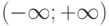 . Является ли произведение функций
. Является ли произведение функций 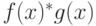 непрерывным на промежутке
непрерывным на промежутке 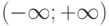 ?
?
Известно, что в точке a предел функции  равен -7, а предел функции
равен -7, а предел функции 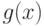 равен 5. Найдите предел
равен 5. Найдите предел  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.

Используя дифференцирование неявной функции, найдите значение производной 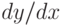 , при условии, что неявная функция задана уравнением
, при условии, что неявная функция задана уравнением 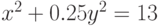 . Найти
. Найти 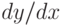 в точке
в точке 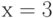 ,
, 
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси 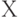 ), заданной уравнением
), заданной уравнением 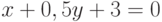 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите ординату точки, в которой прямая, заданная уравнением  , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде рациональной дроби.
В специальной теории относительности масса предмета, который двигается со скоростью 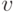 дается формулой:
дается формулой: . Где
. Где  – скорость света,
– скорость света,  – масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,2% по сравнению с массой покоя? Для ответа введите отношение
– масса покоя.Линеаризовав эту формулу, рассчитайте, с какой скоростью должен двигаться предмет, чтобы его масса увеличилась на 0,2% по сравнению с массой покоя? Для ответа введите отношение
c/v
, округленное до целого числа.Функция 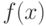 – полином 100 степени, имеющий ровно 100 действительных различных корней. Сколько корней имеет функция
– полином 100 степени, имеющий ровно 100 действительных различных корней. Сколько корней имеет функция 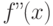 ?
?
Известно, что функция  в точке
в точке  принимает значение
принимает значение 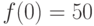 и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 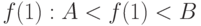 . Найдите
. Найдите 
Постройте равнобедренный треугольник (сторона двух сторон которого равна 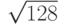 ) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
) с максимально возможной площадью. Чему равна третья сторона такого треугольника?
Вычислите разность между верхней и нижней интегральной суммой для интеграла (при условии разбиения интервала интегрирования на
(при условии разбиения интервала интегрирования на  равных промежутков). Стремится ли эта разность к нулю при
равных промежутков). Стремится ли эта разность к нулю при 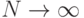

Для функции 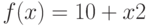 , на интервале
, на интервале 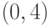 , найдите явно значение функции
, найдите явно значение функции  в точке, существование которой гарантируется теоремой о среднем значении.
в точке, существование которой гарантируется теоремой о среднем значении.
Чему равен наклон прямой (т.е. тангенс угла, образованного прямой с положительным направлением оси 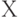 ), заданной уравнением
), заданной уравнением 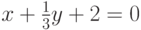 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Найдите уравнение касательной к графику функции 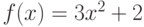 , которая будет параллельная прямой
, которая будет параллельная прямой  . Чему равен наклон касательной? Ответ введите в виде целого числа.
. Чему равен наклон касательной? Ответ введите в виде целого числа.
Пользуясь определением производной, найдите производную функции 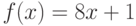 в точке
в точке  . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.
Известно, что функция  в точке
в точке  принимает значение
принимает значение  и, кроме того, ее производная для любого
и, кроме того, ее производная для любого  выражается так:
выражается так:  .Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами
.Из теоремы о среднем значении можно сделать вывод о том, какими целыми числами  и
и  ограничено значение
ограничено значение 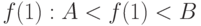 . Найдите
. Найдите 
При помощи какой подстановки можно вычислить следующий интеграл 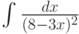 ? Выберите соответствующую вспомогательную переменную из списка
? Выберите соответствующую вспомогательную переменную из списка
Посчитайте, чему равна левая интегральная сумма для интеграла  при разбиении интервала интегрирования на 4 равные части
при разбиении интервала интегрирования на 4 равные части

Найдите точку, в которой касательная к графику функции 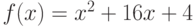 проходит горизонтально. Ответ введите в виде целого числа.
проходит горизонтально. Ответ введите в виде целого числа.
Объект движется по закону 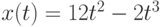 . Чему равна его скорость через две секунды после начала движения, т.е. при
. Чему равна его скорость через две секунды после начала движения, т.е. при  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
Функция задана следующим образом: Найдите значение параметров
Найдите значение параметров  и
и  , при котором функция
, при котором функция  будет и непрерывной в точке
будет и непрерывной в точке  , и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.
, и одновременно дифференцируемой в этой точке.Введите значение параметра а в виде целого числа.

Найдите соотношение высоты H и радиуса основания R цилиндрической банки (т.е. цилиндра без верхней крышки), если известно, что:- ее внутренний объем максимален среди всех возможных банок с одинаковой площадью поверхности А. Подсказка: Используйте R в качестве переменнойВведите значение H, при условии, что 
Ракета взлетает с космодрома вертикально вверх, причем ее высота изменяется со временем по закону  (в метрах). Наблюдатель, находясь на поверхности Земли в 400 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через
(в метрах). Наблюдатель, находясь на поверхности Земли в 400 метрах от точки взлета смотрит на ракету и фиксирует в каждый момент времени угол, который направление на ракету образует с горизонтальной плоскостью. Найдите скорость изменения угла (число радиан в секунду) через 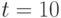 сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
сек. после старта. Ответ введите в форме простой дроби, например, 1/3.
Найдите значение выражения (разность значений производной функции в двух точках) 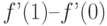 , если функция
, если функция  определяется как
определяется как 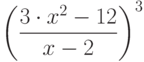
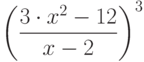
Аппроксимируйте функцию 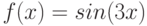 в точке
в точке  линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
линейной функцией. Чему равен наклон прямой, который задает эта линейная функция?
Вычислите интеграл, используя геометрические соображения (т.е. вычисляя площадь соответствующей фигуры) 


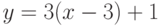 . Отметьте точки, через которые проходит эта прямая:
. Отметьте точки, через которые проходит эта прямая: . Как расположена эта прямая?
. Как расположена эта прямая? дифференцируемой в точке
дифференцируемой в точке 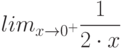
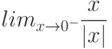
 ?
?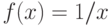 непрерывной на незамкнутом промежутке
непрерывной на незамкнутом промежутке 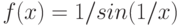 в точке
в точке 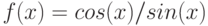 в точке
в точке 

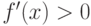 при
при 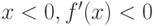 при
при 
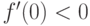
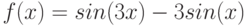 , оцените поведение
, оцените поведение 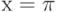
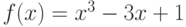 .
.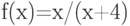 в точке
в точке 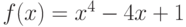 при стремлении
при стремлении  ?
?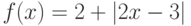 на интервале
на интервале  ?
? .
.
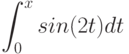
![\int^x_0 [sin(t)-1]dt](https://intuit.ru//sites/default/files/tex_cache/f2533515125cf2a0cdbcdcb9b0776d4d.png)

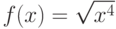 ?
?


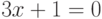 . Как расположена эта прямая?
. Как расположена эта прямая? в точке
в точке 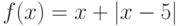 в точке
в точке 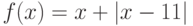 в точке
в точке  в точке
в точке 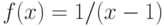 в точке
в точке 

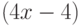 при стремлении
при стремлении 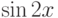 при стремлении
при стремлении 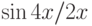 при стремлении
при стремлении 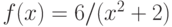 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.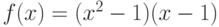 не является непрерывной? Ответ введите в виде целого числа.
не является непрерывной? Ответ введите в виде целого числа.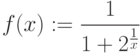
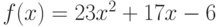 в точке
в точке  в точке
в точке 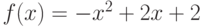 в точке
в точке 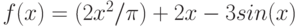 в точке
в точке 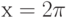
 в точке
в точке 
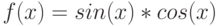 в точке
в точке 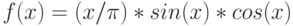 в точке
в точке 
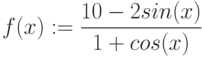
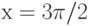
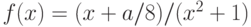 параллельна оси
параллельна оси ![g(f(x))=[f(x)]^3](https://intuit.ru//sites/default/files/tex_cache/88bfa16c60f739905eba0494af1a59f0.png) в точке
в точке 
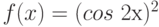 в точке
в точке 



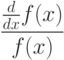
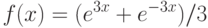
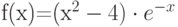




 в точке
в точке  в точке
в точке 
 в точке
в точке  в точке
в точке  линейной функцией
линейной функцией 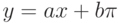 . Чему равно значение a?
. Чему равно значение a? линейной функцией
линейной функцией 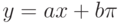 . Чему равно значение
. Чему равно значение 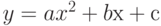 . Чему равно значение
. Чему равно значение 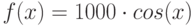 в точке
в точке 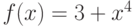 в точке
в точке 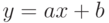 . Чему равно значение
. Чему равно значение  пересекает ось
пересекает ось 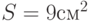
 на интервале
на интервале ![(0,1]](https://intuit.ru//sites/default/files/tex_cache/668c7b55a37300c330dcd565d9e076da.png)
 в точке
в точке 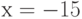 в виде
в виде 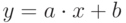 . Чему равно число
. Чему равно число 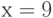 в виде
в виде 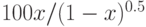 в точке
в точке  в точке
в точке 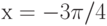
![ln[sin(x)]](https://intuit.ru//sites/default/files/tex_cache/059d9e274b543cf142891b4b7f78dd4d.png) в точке
в точке 
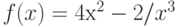 в точке
в точке 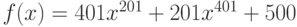 . Полином какой степени получается в результате?
. Полином какой степени получается в результате? , как функцию
, как функцию 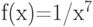 . В качестве ответа введите полученную степень
. В качестве ответа введите полученную степень  , как функцию
, как функцию 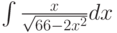 , как функцию
, как функцию 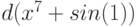 в формате
в формате 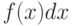 . Чему равно значение
. Чему равно значение 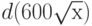 в формате
в формате 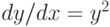 с начальным условием
с начальным условием  . Вычислите, чему равно значение
. Вычислите, чему равно значение  .
. с начальным условием
с начальным условием  . Вычислите, чему равно значение
. Вычислите, чему равно значение 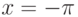 .
.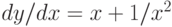 с начальным условием
с начальным условием  . Вычислите, чему равно значение
. Вычислите, чему равно значение 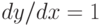 с начальным условием
с начальным условием 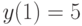 . Вычислите, чему равно значение
. Вычислите, чему равно значение 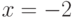 .
.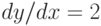 с начальным условием
с начальным условием  с начальным условием
с начальным условием 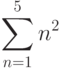


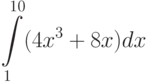






 для
для 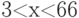

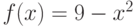 .
.
 и
и 

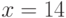
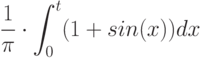

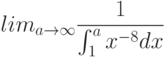
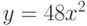 и
и 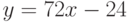 ?
?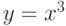 и
и 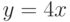 ?
?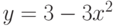 ?
?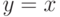 , от
, от 

 и прямой линией
и прямой линией 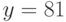 ?
? в точке
в точке 
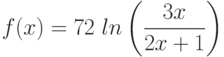
 при
при 
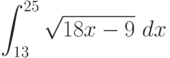
![\int ^{\sqrt{28/3}}_{\sqrt {3}}[32x \cdot(3x^2-1)^{1/3} ]\ dx](https://intuit.ru//sites/default/files/tex_cache/a06bf90e72e20b7514b985b71c8cb580.png)
![\int ^{4}_{1}\left[\frac{5120}{x^2} \cdot(1+ \frac{1}{x})^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/2d7ac9ec1be2b39113cf7d0b74508b46.png)
![\int ^{e^4}_{e^2}\left[\frac{12}{x \cdot ln(x)}\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/add2e6ab56616b9ad20c34ec2d8f3a90.png)

![\int^{\pi/2}_{0} \left[ \frac {256}{\pi}\cdot(sin\ x)^6\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/09d1a0ca896f1ce75c4a9d802d649d92.png)
![\int^{\pi/2}_{0} [x \cdot sin\ x]\ dx](https://intuit.ru//sites/default/files/tex_cache/c9618e986dce17800fbbe09eb8981101.png)

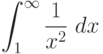
![\int^{1}_{0} [ln\ x]^4\ dx](https://intuit.ru//sites/default/files/tex_cache/e40e770fcd13c7f8292c4a39f9731231.png)


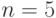

![\frac{1}{tg(\int^1_{-1}[\frac{1}{x^2+4}]dx)}](https://intuit.ru//sites/default/files/tex_cache/6c3ffa1c0b7adeb063a145742f159255.png)



![\int^e_1\frac{72}{x}[ln(x)]^{5/3}dx](https://intuit.ru//sites/default/files/tex_cache/74f1d2d996922e9ea0f6f84d3ef86a75.png)



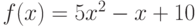 в точке
в точке 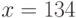

 в точке
в точке 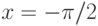 .
.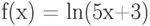 в точке
в точке  в точке
в точке  при
при 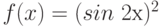 в точке
в точке 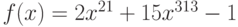 пересекает ось
пересекает ось  линейной функцией
линейной функцией 
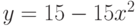 ?
?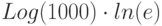
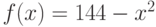 .
. не является непрерывной? Ответ введите в виде целого числа.
не является непрерывной? Ответ введите в виде целого числа. . Отметьте точки, через которые проходит эта прямая:
. Отметьте точки, через которые проходит эта прямая: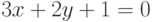 . Как расположена эта прямая?
. Как расположена эта прямая?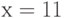 . Ответ введите в виде целого числа.
. Ответ введите в виде целого числа.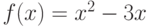 в точке
в точке 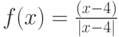 дифференцируемой в точке
дифференцируемой в точке  в точке
в точке 

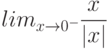
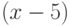 при стремлении
при стремлении 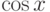 при стремлении
при стремлении 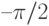 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.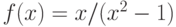 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.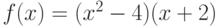 не является непрерывной? Ответ введите в виде целого числа.
не является непрерывной? Ответ введите в виде целого числа. ?
?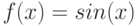 непрерывной на промежутке
непрерывной на промежутке  в точке
в точке 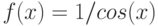 в точке
в точке 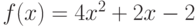 в точке
в точке 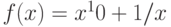

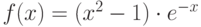
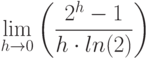
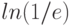
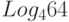
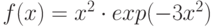

 линейной функцией
линейной функцией 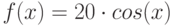 в точке
в точке 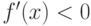 при
при 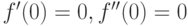
 .
.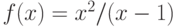 в точке
в точке 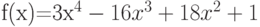 при стремлении
при стремлении  в виде
в виде 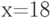 в виде
в виде 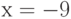
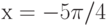

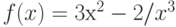 в точке
в точке 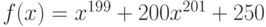 . Полином какой степени получается в результате?
. Полином какой степени получается в результате? . В качестве ответа введите полученную степень
. В качестве ответа введите полученную степень 
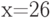
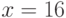 ?
?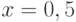 .
.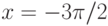 .
.


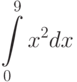


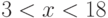
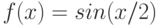
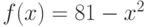 .
.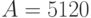
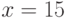
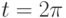

 ?
?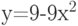 ?
?

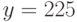 ?
? в точке
в точке 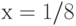

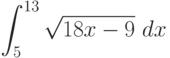
![\int ^{\sqrt{28/3}}_{\sqrt {3}}[16x \cdot(3x^2-1)^{1/3} ]\ dx](https://intuit.ru//sites/default/files/tex_cache/217c95faf600464548f7e45b77b51034.png)
![\int ^{1/3}_{1}\left[\frac{5}{x^2} \cdot(1+ \frac{1}{x})^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/1c818716711630d33f893e392f485054.png)
![\int ^{e^3}_{e^2}\left[\frac{12}{x \cdot ln(x)}\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/1baeb43f2328646c69df5ba4925a9fa8.png)
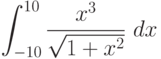
![\int^{\pi/2}_{0} \left[ \frac {256}{\pi}\cdot(cos\ x)^8\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/9ab65bd716be2524acda3c3bc5fc373a.png)
![\int^{\pi}_{0} [\frac {x}{\pi} \cdot sin\ x]\ dx](https://intuit.ru//sites/default/files/tex_cache/c0bd2806049ccf1ba5aa0a3f934a3d09.png)



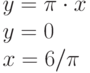
![\frac{1}{tg(\int^5_{-5}[\frac{1}{x^2+4}]dx)}](https://intuit.ru//sites/default/files/tex_cache/e69dce4c9d6833608dc5747753e9ea85.png)
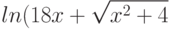
![\int^e_1\frac{13}{x}[ln(x)]^{9/4}dx](https://intuit.ru//sites/default/files/tex_cache/7acd872803018174fbe706833577dffb.png)


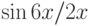 при стремлении
при стремлении ![\int ^{e^4}_{e}\left[\frac{12}{x \cdot ln(x)}\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/33038445a0d31acc19e95133d2b0eb73.png)
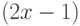 при стремлении
при стремлении 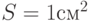
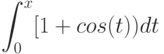
 в точке
в точке 



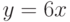 ?
?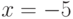
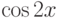 при стремлении
при стремлении 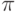 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.
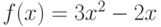 в точке
в точке 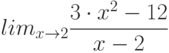
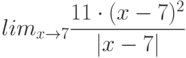
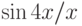 при стремлении
при стремлении 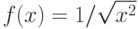 ?
?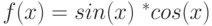 непрерывной на промежутке
непрерывной на промежутке 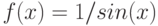 в точке
в точке 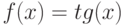 в точке
в точке 
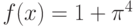 в точке
в точке 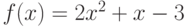 в точке
в точке 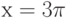
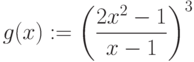



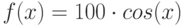 в точке
в точке 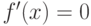 при
при 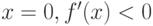 при
при 
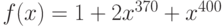 пересекает ось
пересекает ось 
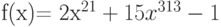 . Полином какой степени получается в результате?
. Полином какой степени получается в результате? .
.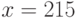
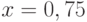 .
.

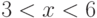

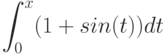
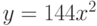 и
и  ?
?

 при
при ![\int ^{\sqrt{28/3}}_{\sqrt {3}}[24x \cdot(3x^2-1)^{1/3} ]\ dx](https://intuit.ru//sites/default/files/tex_cache/df6b292127195b539393e8be6379d575.png)
![\int ^{3}_{1}\left[\frac{1215}{x^2} \cdot(1+ \frac{1}{x})^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/0a6235f9b8695331accb2942604f5f20.png)
![\int^{\pi/2}_{0} [\frac {2x}{\pi} \cdot sin\ x]\ dx](https://intuit.ru//sites/default/files/tex_cache/deea2e6fcccfde5705b9e56460a6e48e.png)
![\int^{1}_{0} [ln\ x]^3\ dx](https://intuit.ru//sites/default/files/tex_cache/e78502c26fecda8df3df34808dfa52f5.png)
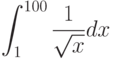

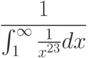

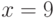 ?
? и
и  ?
?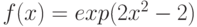
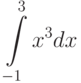


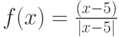 дифференцируемой в точке
дифференцируемой в точке 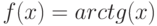 в точке
в точке 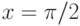 .
.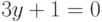 . Как расположена эта прямая?
. Как расположена эта прямая?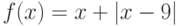 в точке
в точке 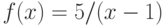 в точке
в точке 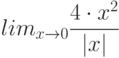
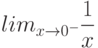
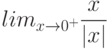
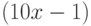 при стремлении
при стремлении 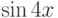 при стремлении
при стремлении  ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа. ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.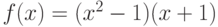 не является непрерывной? Ответ введите в виде целого числа.
не является непрерывной? Ответ введите в виде целого числа.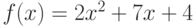 в точке
в точке 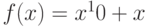
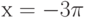
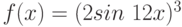 в точке
в точке 







 пересекает ось
пересекает ось 
![(0,2]](https://intuit.ru//sites/default/files/tex_cache/eb1351ddf84d6ca6e06bbb319592766d.png)
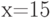 в виде
в виде  в точке
в точке 
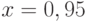 .
.

 .
.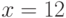
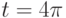
 ?
?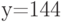 ?
? в точке
в точке  при
при ![\int ^{2}_{1}\left[\frac{160}{x^2} \cdot(1+ \frac{1}{x})^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/8cb0381fe49735830438eb7dd140e054.png)
![\int ^{e^3}_{e}\left[\frac{12}{x \cdot ln(x)}\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/0923b04e6b7391d488bcf4c9e264c304.png)
![\int^{2\pi}_{0} [\frac {x}{\pi} \cdot sin\ x]\ dx](https://intuit.ru//sites/default/files/tex_cache/42b90a273a1aa7dffb43eb7c33e1472b.png)

![\int^{1}_{0} [ln\ x]^2\ dx](https://intuit.ru//sites/default/files/tex_cache/877214570aaed0decaef373c94d0a19e.png)

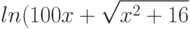

![\int^e_1\frac{7}{x}[ln(x)]^{5/2}dx](https://intuit.ru//sites/default/files/tex_cache/2c9ba9a4dad591bbdb85712382dbfc8d.png)

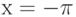
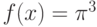 в точке
в точке 
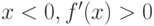 при
при 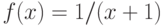 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.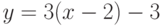 . Отметьте точки, через которые проходит эта прямая:
. Отметьте точки, через которые проходит эта прямая: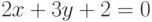 . Как расположена эта прямая?
. Как расположена эта прямая? в точке
в точке 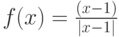 дифференцируемой в точке
дифференцируемой в точке 
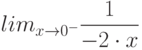
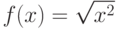 ?
? в точке
в точке 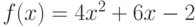 в точке
в точке 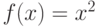 в точке
в точке 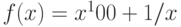
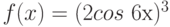 в точке
в точке 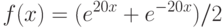

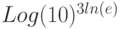

 в точке
в точке  на интервале
на интервале  ?
?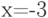
 . Полином какой степени получается в результате?
. Полином какой степени получается в результате?
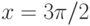 .
.

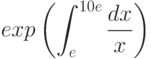
 при
при 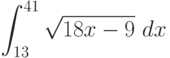
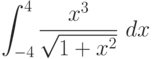


![\int^{1}_{0} [ln\ x]^5\ dx](https://intuit.ru//sites/default/files/tex_cache/e44f2cffcd3c8465dbd99f8a6d27a5ce.png)
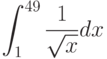

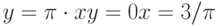
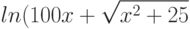
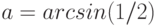

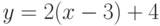 . Отметьте точки, через которые проходит эта прямая:
. Отметьте точки, через которые проходит эта прямая: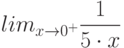
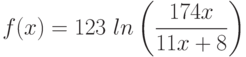
![\int^{1}_{0} [ln\ x]^6\ dx](https://intuit.ru//sites/default/files/tex_cache/3f95592f9a05b4283a366dfd91f5a7ec.png)
![\int ^{\sqrt{28/3}}_{\sqrt {3}}[40x \cdot(3x^2-1)^{1/3} ]\ dx](https://intuit.ru//sites/default/files/tex_cache/9b28fa35d548e72309685e8e47b60ca0.png)
 при стремлении
при стремлении  в точке
в точке 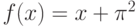 в точке
в точке 

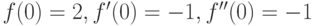
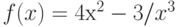 в точке
в точке 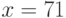

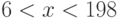

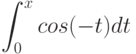
 и
и  ?
?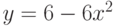 ?
?
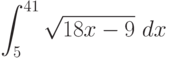

![\int^{\pi/2}_{0} \left[ \frac {256}{\pi}\cdot(sin\ x)^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/1ea1f24e19ff40967aa53c706d1f2dff.png)
![\frac{4}{tg(\int^2_{-4}[\frac{1}{x^2+4}]dx)}](https://intuit.ru//sites/default/files/tex_cache/f84e89c1b0950991ada22498bc0841d5.png)
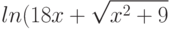
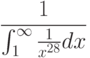
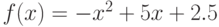 в точке
в точке 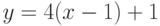 . Отметьте точки, через которые проходит эта прямая:
. Отметьте точки, через которые проходит эта прямая: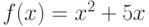 в точке
в точке 

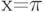 линейной функцией
линейной функцией 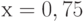
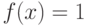 .
.
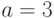 и
и 
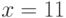
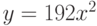 и
и  ?
? ?
?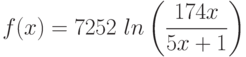
![\int ^{\sqrt{28/3}}_{\sqrt {3}}[8x \cdot(3x^2-1)^{1/3} ]\ dx](https://intuit.ru//sites/default/files/tex_cache/d33eb00c9ead2f19ff54f2da973b7e01.png)
![\int ^{e^2}_{e}\left[\frac{12}{x \cdot ln(x)}\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/cc37249196dcd5968edb7b7cf12c9349.png)

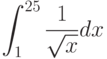
![\frac{1}{tg(\int^2_{-2}[\frac{1}{x^2+4}]dx)}](https://intuit.ru//sites/default/files/tex_cache/6edd85e6a42b63216e2f37a809d8053d.png)
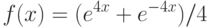

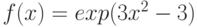
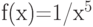 . В качестве ответа введите полученную степень
. В качестве ответа введите полученную степень  не является непрерывной? Ответ введите в виде целого числа.
не является непрерывной? Ответ введите в виде целого числа. в точке
в точке 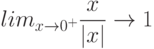
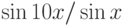 при стремлении
при стремлении 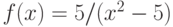 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа. линейной функцией
линейной функцией 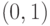 ?
?
 и
и 
![\int^x_0 [1-cos(t)]dt](https://intuit.ru//sites/default/files/tex_cache/4bfa096d381efa4d4e8b6e3522d1a7b2.png)
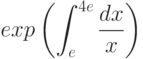

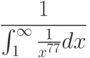

 в точке
в точке 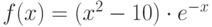
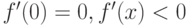 при
при 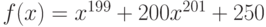 пересекает ось
пересекает ось ![\int^{\pi}_{0} [x \cdot sin\ x]\ dx](https://intuit.ru//sites/default/files/tex_cache/89a5589cbf83ffcc7f1e4b91d9dd5fc3.png)
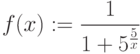
 в точке
в точке 
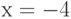
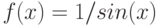 непрерывной на промежутке (0, 3)?
непрерывной на промежутке (0, 3)? непрерывной на незамкнутом промежутке (0, 1)?
непрерывной на незамкнутом промежутке (0, 1)?
 в точке
в точке 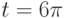
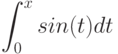

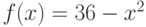 .
. ?
?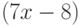 при стремлении
при стремлении 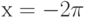
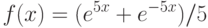
 при
при ![\int ^{1/2}_{1}\left[\frac{5}{x^2} \cdot(1+ \frac{1}{x})^4\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/6fa3b18358c6bf6438053819f767f97d.png)
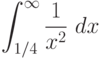
![\int^e_1\frac{5}{x}[ln(x)]^{3/2}dx](https://intuit.ru//sites/default/files/tex_cache/8a13a25fdfb36f83472e5e34767e8230.png)


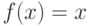 . В качестве ответа введите полученную степень
. В качестве ответа введите полученную степень 
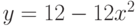 ?
?![\int^{\pi/2}_{0} \left[ \frac {256}{\pi}\cdot(cos\ x)^6\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/e16402194e8fdc9c060df1ca15dd34c6.png)
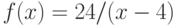
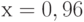
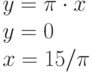
![\frac{1}{tg(\int^3_{-3}[\frac{1}{x^2+4}]dx)}](https://intuit.ru//sites/default/files/tex_cache/52bdf1c512f7ff1b4223dd9f93294ab8.png)

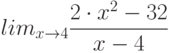
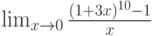
![\int^{\pi/2}_{0} \left[ \frac {256}{\pi}\cdot(sin\ x)^8\right]\ dx](https://intuit.ru//sites/default/files/tex_cache/1bf5fc840ca199c8d12e84d579d16a47.png)

 при
при 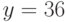 ?
? в точке
в точке 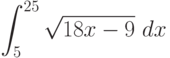
 , пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа.
, пересекает ось ординат (т.е. ось ОY)? Ответ введите в виде целого числа. в точке
в точке 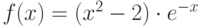
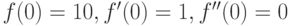
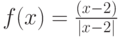 дифференцируемой в точке
дифференцируемой в точке 
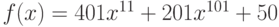 . Полином какой степени получается в результате?
. Полином какой степени получается в результате?
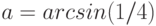
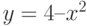
 ? Ответ введите в виде целого числа.
? Ответ введите в виде целого числа.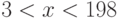
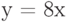 ?
?![\int^e_1\frac{9}{x}[ln(x)]^{5/4}dx](https://intuit.ru//sites/default/files/tex_cache/c4fdc3ac18da9037aa63ddc5ae49a9b4.png)