Введение в математическое программирование

Если функция f(x₁,...,x_n) в некоторой внутренней точке 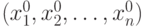$(x^0_1, x^0_2, \ldots, x^0_n)$ допустимой области R функция достигает относительного максимума и при этом справедливо равенство ∂f(x₀)/∂x_j = 0, j=1,...,n, то:

(Отметьте один правильный вариант ответа.)

Варианты ответа

функция дифференцируема в данной области(Верный ответ)

функция частично дифференцируема в данной области

функция не дифференцируема в данной области

Похожие вопросы

Пусть f(x₁,...,x_n) дифференцируема в некоторой допустимой области R. Если в некоторой внутренней точке $(x^0_1, x^0_2, \ldots, x^0_n)$ области R функция достигает относительного максимума, то:

Пусть f(x₁,...,x_n) дифференцируема в некоторой допустимой области R. Если для данной функции выполняется условие ∂f(x₀)/∂x_j = 0, j=1,...,n, то в некоторой внутренней точке $(x^0_1, x^0_2, \ldots, x^0_n)$ области R функция:

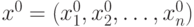Функция f(x) достигает локального максимума в точке $x^0 = (x^0_1, x^0_2 ,\ldots, x^0_n)$ и при этом имеет место равенство $f(x^0_1, x^0_2 ,\ldots, x^0_n) \ge; f(x_1, x_2, \ldots, x_n)$ . Это справедливо:

Функция f(x) достигает локального максимума в точке $x^0 = (x^0_1, x^0_2 ,\ldots, x^0_n)$ , если для всех точек x, лежащих в малой окрестности точки $[x^0_1, x^0_2 ,\ldots, x^0_n ]$ имеет место неравенство:

Функция f(x) достигает глобального (абсолютного) максимума в точке x⁰, если для всех точек x є R справедливо:

Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . При этом A_r не входит в базис, т.е. справедливо равенство: A₁x_1r+A₂x_2r+...+A_mx_mr = A_r. Тогда базисное решение имеет вид:

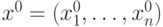Если для некоторой строго вогнутой функции f(x) в некоторой окрестности точки $x^0 = (x^0_1,\ldots, x^0_n)$ знаки определителей чередуются, т.е. справедливо условие $f_{11}(x_0) < 0; \quad\begin{vmatrix}f_{11}(x_0) & f_{12}(x_0) \\f_{21}(x_0) & f_{22}(x_0)\end{vmatrix}> 0 ; \quad\begin{vmatrix}f_{11}(x_0) & f_{12}(x_0) & f_{13}(x_0) \\f_{21}(x_0) & f_{22}(x_0) & f_{23}(x_0) \\f_{31}(x_0) & f_{32}(x_0) & f_{33}(x_0) \end{vmatrix}< 0$ , то функция f(x):

Если для некоторой функции f(x) в некоторой окрестности точки $x^0 = (x^0_1,\ldots, x^0_n)$ знаки определителей чередуются, т.е. справедливо условие $f_{11}(x_0) < 0; \quad\begin{vmatrix}f_{11}(x_0) & f_{12}(x_0) \\f_{21}(x_0) & f_{22}(x_0)\end{vmatrix}> 0 ; \quad\begin{vmatrix}f_{11}(x_0) & f_{12}(x_0) & f_{13}(x_0) \\f_{21}(x_0) & f_{22}(x_0) & f_{23}(x_0) \\f_{31}(x_0) & f_{32}(x_0) & f_{33}(x_0) \end{vmatrix}< 0$ , то дифференцируемая функция f(x):

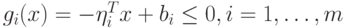Рассмотрим задачу нелинейного программирования: минимизировать f(x) при $g_i(x) = - \eta^T_i x + b_i \le 0, i = 1,\ldots,m$ . Известно, что существует множество неотрицательных скаляров {λ_i} ≥ 0, для которых справедливо соотношение Δf(x^*)=Σλ_iη_i(x) = -Σλ_iΔg_i(x^*), i є I. Тогда для входящего вектора справедливо условие:

Если для всех точек x є R некоторой функции f(x) справедливо неравенство f(x⁰) ≥ f(x), то в точке x⁰ функция f(x):