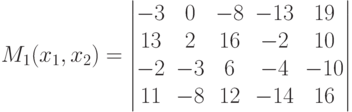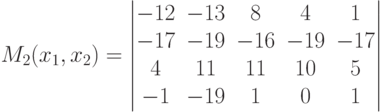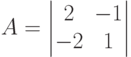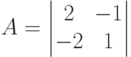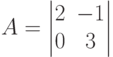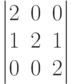Пусть в конечной игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> X1={1,2,3,4}, X2={1,2,3,4,5}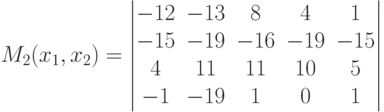 Укажите стратегии второго игрока, являющиеся наилучшими по гарантированному результату
Укажите стратегии второго игрока, являющиеся наилучшими по гарантированному результату
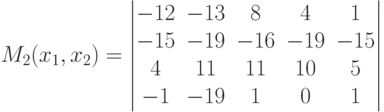
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
третья стратегия
пятая стратегия(Верный ответ)
первая стратегия(Верный ответ)